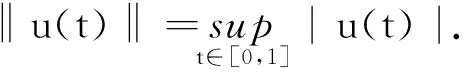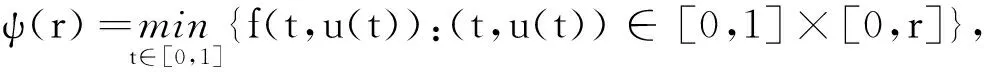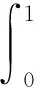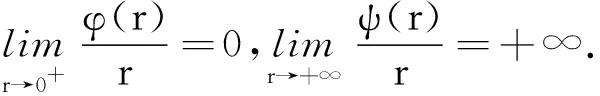一类非线性分数阶微分方程正解的存在性*

施 敏

(南京财经大学应用数学学院，江苏 南京 210023)

1 问题的提出

分数阶微积分理论是当今数学界的一个热点话题，它在流体力学、生物进化、高分子材料和图像处理等领域有极其重要的应用.伴随着非线性科学的发展，研究分数阶微分方程及其边值问题，对解决非线性问题的意义越来越大.目前，很多学者[1-4]采用非线性分析的方法(如不动点定理和Leray-Schauder度理论等)探讨分数阶微分方程边值问题1个或多个正解的存在性.受文献[1]的启发，笔者将研究如下具有积分边值条件的Caputo型非线性分数阶微分方程的边值问题：

(1)

其中：0<λ

2 预备知识

定义1[5]函数f:[0,+∞)→R的α(α>0)阶Caputo型微分定义为

其中[α]为实数α的整数部分.

定义2[5]函数f:[0,+∞)→R的α(α>0)阶Riemann-Liouville型积分定义为

等式右边在(0,+∞)上是逐点定义的.

定义3[5]函数f:[0,+∞)→R的α(α>0)阶Riemann-Liouville型导数定义为

等式右边在(0,+∞)上是逐点定义的.

引理3[7]设n<α

(2)

(3)

证明根据引理2，问题(2)中的等式CDαu(t)+y(t)=0等价于

由条件u(0)=u′(0)=…=u(k-1)(0)=u(k+1)(0)=…=u(n)(0)=0，可得

因此

(4)

从而解得

(5)

将(5)式代入(4)式，可得

引理3得证.

引理4[1]设n<α

(1)对于∀t,s∈[0,1],λ≠k+1，有G(0,s)=G(t,1)=0；

(2)对于∀s∈[0,1]，有G(1,s)=0当且仅当λ=0；

(3)对于∀s∈(0,1)，有G(1,s)>0当且仅当λ∈(0,k+1)；

(4)对于∀t∈(0,1)，有G(t,0)>0当且仅当λ∈[0,k+1)；

(5)对于∀t,s∈(0,1)，有G(t,s)>0当且仅当λ∈[0,k+1)；

引理5设n<α

证明首先考虑0≤t≤s≤1的情况.令

由0≤t≤s≤1,n<α

然后考虑0≤s≤t≤1的情况.令

由0≤s≤t≤1,n<α

断言h(t,s)>tk,∀0

对一切0v,∀0tk,∀0

引理5得证.

(ⅰ)‖(Tu)(t)‖≥‖u(t)‖,u(t)∈P∩∂Ω1,且‖(Tu)(t)‖≤‖u(t)‖,u(t)∈P∩∂Ω2;

(ⅱ)‖(Tu)(t)‖≤‖u(t)‖,u(t)∈P∩∂Ω1,且‖(Tu)(t)‖≥‖u(t)‖,u(t)∈P∩∂Ω2.

3 主要结果及其证明

并记

定理1算子T:P→P是全连续的.

和

因此T(P)⊂P.

然后由函数G(t,s)和f(t,u(t))的连续性可知算子T:P→P是连续的.

故集合T(Ω)在X中有界.对于∀u(t)∈Ω，有

定理1证毕.

定理2假定如下条件之一成立：

则问题(1)在P中至少有1个解.

定理2证毕.