基于改进型显性互补滤波的MENS姿态解算

付 雷，章 政，余 义

（武汉科技大学 信息科学与工程学院，武汉 430080）

对于移动机器人、飞行器和卫星通信等系统而言，实时、准确的姿态估计是实现各种载体稳定运行的有效前提之一。

目前，由低成本、小型化的微机械陀螺仪、加速度计等惯性测量单元IMU（inertial measurement unit）构成的微机电系统MEMS（micro-electro-mechanical system）姿态估计得到了广泛的研究和应用。然而在实际应用过程中，单一的IMU易受到噪声、温度漂移及安装误差等多方面因素影响[1]。因此，将不同的传感器进行优势互补，形成多传感器融合系统用于保证载体姿态的精度和实时性。

1 多传感器融合系统的研究现状

低成本STM32处理器的四旋翼飞行器试验测试平台，将所设计的算法进行静态试验和动态试验，以验证所设计系统的有效性。

在多传感器融合系统中，通常是以卡尔曼滤波算法为基础的扩展和衍生算法或者互补滤波算法，将多种IMU传感器的信息进行融合，由此提高载体姿态的精度和抗干扰性。文献[2]设计了一种卡尔曼滤波算法，将加速度及磁航向作为观测量对姿态信息及陀螺仪的漂移进行修正；文献[3]提出了一种扩展卡尔曼滤波算法，将测量噪声和系统噪声引入状态方程，提高了姿态解算精度，但在观测方程线性的时候引入了误差；文献[4-5]提出了一种无迹卡尔曼滤波算法，解决了线性化带来的误差，相比扩展卡尔曼精度更高；文献[6]设计了一种互补滤波算法，无需对噪声进行精确建模，从频域的角度上消除误差并进行数据融合。在此基础上，文献[7-8]提出了一种显性互补滤波ECF（explicit complementary filter）算法，在互补滤波算法的补偿环节中加入了积分器，直接对IMU所测的矢量数据进行融合。文献[9]提出一种具有增益调节机制的显性互补滤波器，使得基于重力加速度估计的互补滤波器，能获得较为精确的姿态估计。文献[10]给出了一种自适应显性互补滤波算法，根据加速计的输出，判断载体的运动情况，实时调整PI参数，以提高姿态估计的精度。

对于以卡尔曼滤波算法为基础的信息融合方法，由于载体姿态变量的非线性、观测方程的求解，以及系统噪声和测量噪声序列方差阵的计算，其繁琐的计算过程对处理器的运算速度和要求都较高，对于MEMS的实际工程应用难度较大。

相对而言，以互补滤波为基础的相关算法既可解决单一传感器无法准确估计姿态的问题，也无需对姿态估计进行重构，更适用于嵌入式硬件平台。

鉴于此，文中设计了一种加速度计/陀螺仪组合导航的改进型显性互补滤波姿态解算算法。首先，对加速度计量测数据的白噪声进行处理，再将其与陀螺仪数据融合进行姿态解算，由此减小白噪声对姿态解算精度的影响。然后，为了解决滤波后加速度数据对姿态解算的实时性造成的影响，设置缓存区保存更新后的四元数向量，在缓存区中取出与加速度对应时刻的四元数向量进行数据融合。最后，搭建了基于

2 系统姿态描述

在载体的运动状态描述中，定义的导航坐标系（参考坐标系）n系和载体坐标系b系如图1所示。其中，导航坐标系选取“东-北-天”建立坐标系，坐标原点为O点；载体坐标系选取右手直角坐标系，即向右为X正方向，向前为Y轴正方向，向上为Z轴正方向，其坐标原点O′与导航坐标系原点重合。

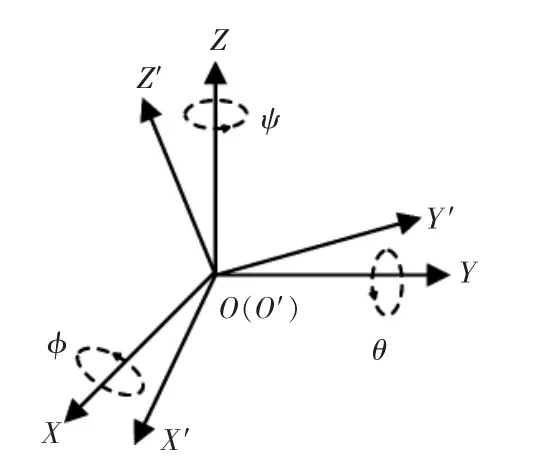
图1 导航坐标系和载体坐标系Fig.1 Navigation coordinate system and carrier coordinate system

在此选用计算量小、算法简单的四元数更新算法[11]实现载体的姿态估计。四元数定义为

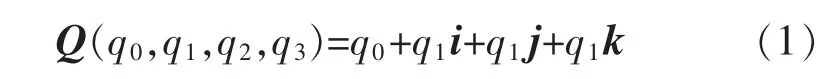
式中：q0，q1，q2，q3为实数；i，j，k 为互相正交的单位向量，且为虚单位

载体的姿态分别用绕Z轴旋转为偏航角（yaw）ψ，绕Y轴旋转为横滚角（roll）θ，绕X轴旋转为俯仰角（pitch）φ来描述，且按照ψ→θ→φ的旋转顺序。将四元数转化为欧拉角形式的方向余弦矩阵为

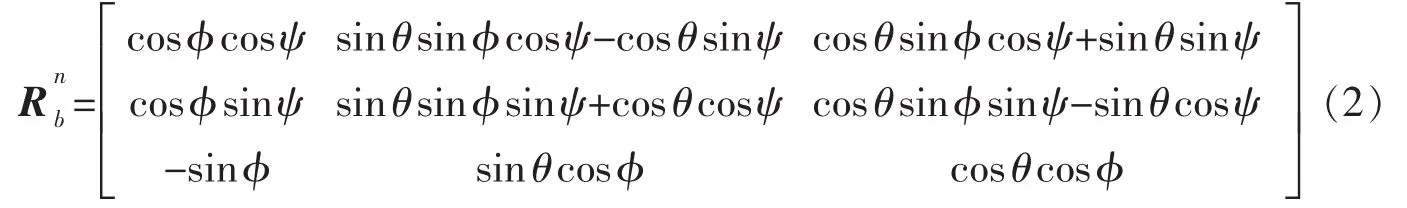
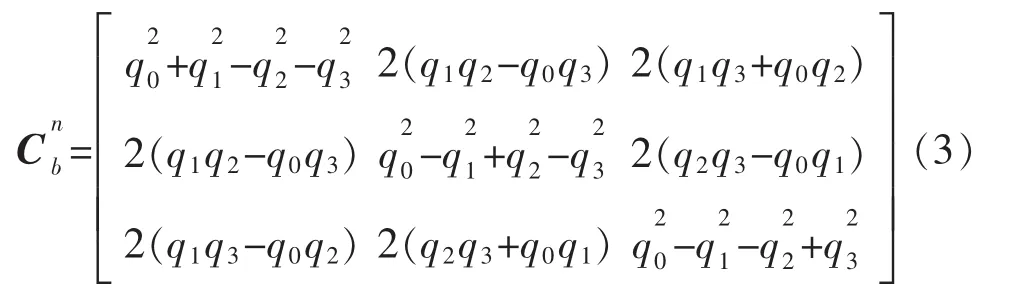
由式（2）（3）可得，四元数与欧拉角的关系为

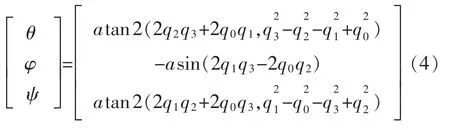
3 基于改进显性互补滤波器姿态估计算法

3.1 陀螺仪姿态更新算法

四元数的运动学微分方程为

其中

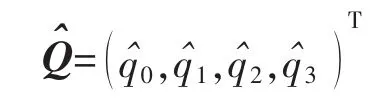
由式（5），可得载体的四元数更新等式为

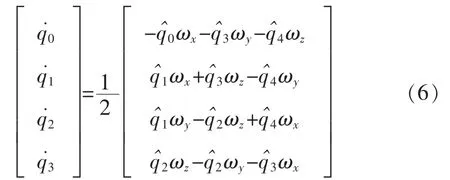
假设，四元数更新时间及采样时间为T，在时间间隔（t，t+T）内，ω 为常数，载体四元数的更新迭代公式为

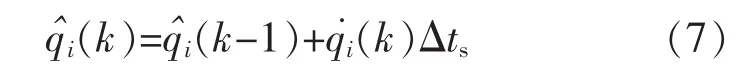
式中：i=1，2，3；Δts为系统采样时间。

根据更新后t时刻的四元数，可得到载体的旋转矩阵，由式（4）得到t时刻载体的姿态角。

3.2 改进显性互补滤波器设计

显性互补滤波器是在速度计/陀螺仪互补滤波算法的补偿环节中加入积分环节，由此补偿陀螺仪产生的漂移误差。同时，为了减小加速度原始数据中白噪声对姿态解算精度造成的干扰，在显性互补滤波算法的基础上，消除低通滤波器延时给姿态解算实时性带来的影响，文中所设计的改进显性互补滤波算法如图2所示。

利用该算法进行四旋翼姿态解算的具体步骤如下：

初始化四元数，令

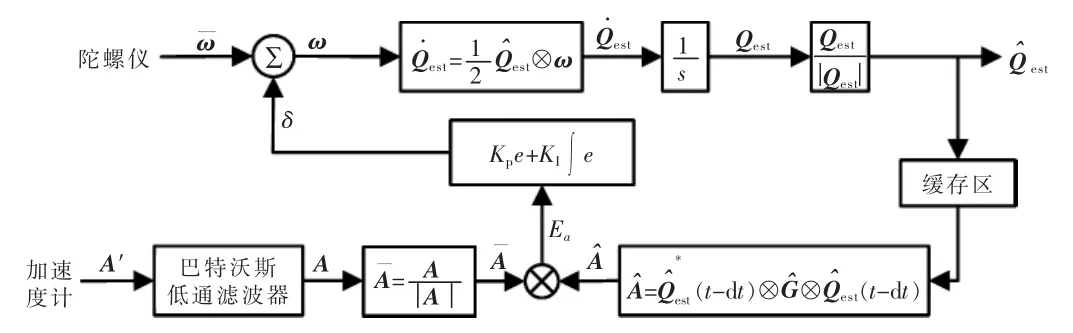
图2 改进显性互补滤波器Fig.2 Improved explicit complementary filter

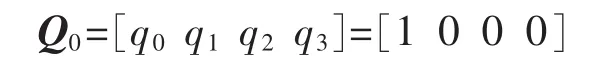
将测得的载体坐标系下的加速度A′经过巴特沃斯低通滤器后进行标准化，得到载体坐标系下三轴加速度的分量构成的向量

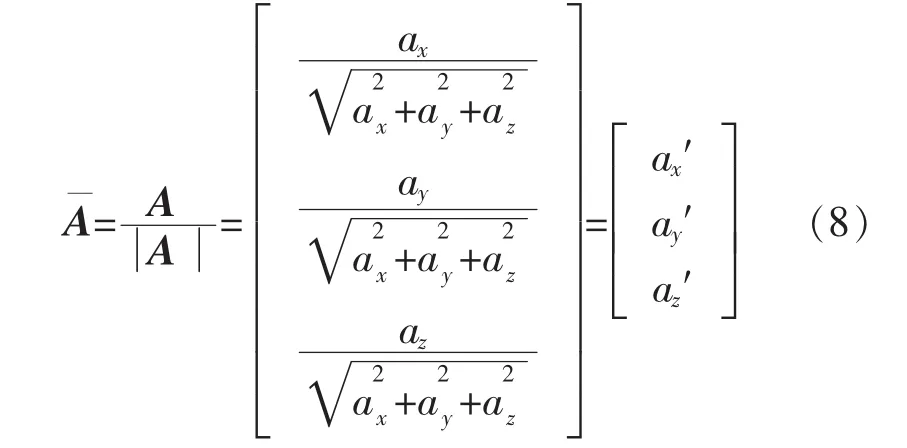
式中：ax′，ay′，az′分别为三轴加速度分量。 但信号经过巴特沃斯低通滤波器之后存在延时，这种特性称为滤波器的群时延，其定义[12]为

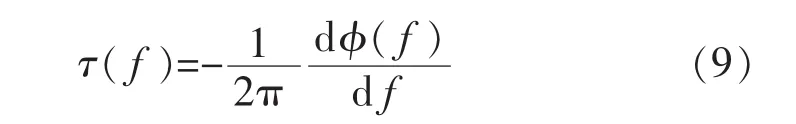
式中：φ（f）为滤波器相位响应；f为频率。为了消除群时延对姿态解算实时性的影响，需求出延时时间。通过式（9）计算出加速度延时时间为Δt，在缓存

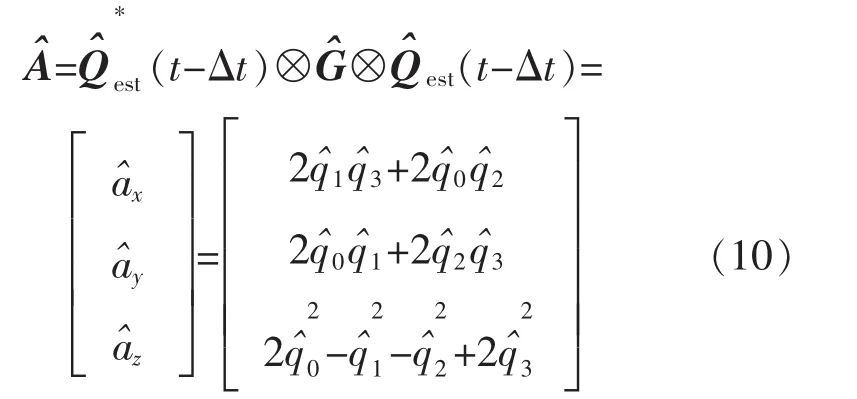
其中

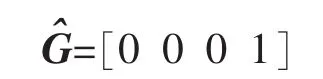
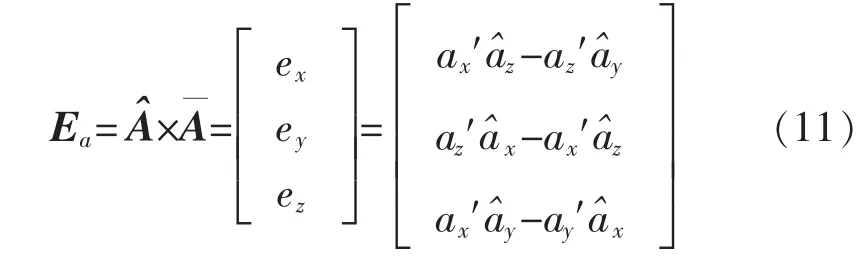
为了对陀螺仪的输出进行预测矫正，误差向量经过PI环节得到的校正量δ为

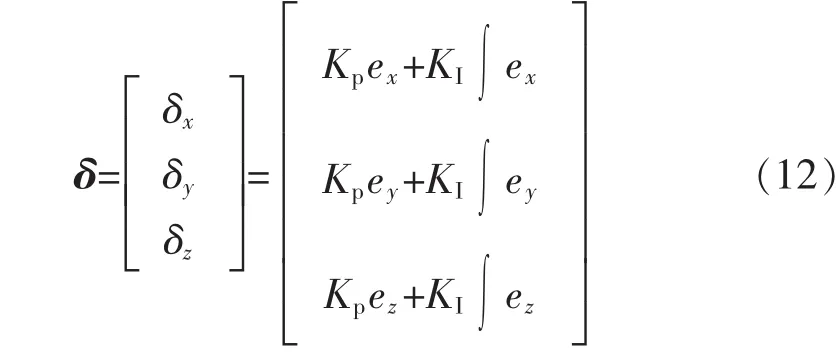
显示互补滤波器的效果与KP，KI的选择有很大的关系，如果参数不合适，则姿态估计的误差较大，甚至偏离实际值。KP为低通滤波器和高通滤波器的之间的转接频率，根据加速度计的输出A′和陀螺仪的输出ω的频率特性来选取；KI为积分增益，其值为Kp的几十或几百分之一。

最后，将陀螺仪测得的角速度与式（11）中所求的校正量相加，得到补偿后的三轴角速度为

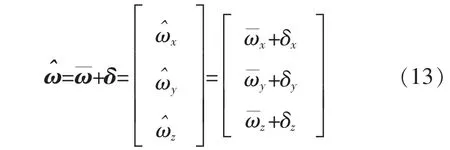
将补偿后的三轴角速度代入式（6），求得更新后的姿态四元数微分；利用式（7）对四元数微分进积分，积分时间为采样周期，根据更新后的四元数可得到对应的旋转矩阵，进而通过式（4）得到四旋翼的姿态角 θ，ψ，φ。

4 试验测试平台

文中所搭建的四旋翼飞行器试验测试平台如图3所示；建立了上位机、飞行器和遥控器通讯，系统结构如图4所示。

图3 四旋翼飞行器实物Fig.3 Four-rotor aircraft object

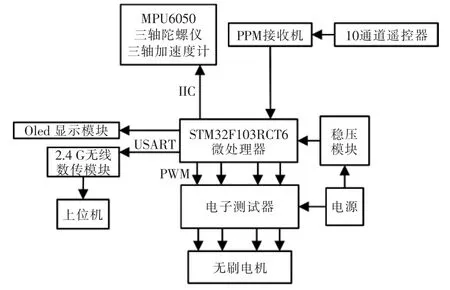
图4 飞控系统结构Fig.4 Flight control system structure

图4中，四旋翼飞行器的控制单元由主控模块、惯性测量模块、稳压模块、电源模块、电机驱动模块和无线通讯模块构成。其中，主控模块选用ST公司的基于ARM-CortexM3内核的STM32F103RCT6芯片。惯性测量模块选用美国Inven Sense公司的三轴陀螺仪和三轴加速度计集成芯片MPU6050，与主控模块通过IIC进行通讯。无线通讯模块选用富斯公司的10通道2.4 GHz遥控器与PPM接收器，以及2.4 GHz无线数传模块，PPM信号通过单个I/O口就能与主控通讯，无线传输距离可达700 m，无线数传模块通过串口与主控模块通讯，发送实时姿态数据到上位机。电机驱动模块则利用PWM控制电子调速器的输出来驱动无刷电机。四旋翼飞行器的各项参数见表1。

表1 四旋翼飞行器参数Tab.1 Parameters of quadrotor

5 试验结果及分析

为了测得噪声的频率范围，让四旋翼飞行器处于悬停状态，对加速度计的原始测量值进行采集，将采集到的数据通过USART上传到上位机，并进行FFT变换。根据频谱分析，可以确定截止频率约为20 Hz，所以试验选用了截止频率为20 Hz的二阶巴特沃斯数字低通滤波器来进行噪声处理。采用MatLab仿真出幅频和相频特性曲线，如图5所示。根据3.2的分析，由式（9）可求得延时时间约为64 ms。

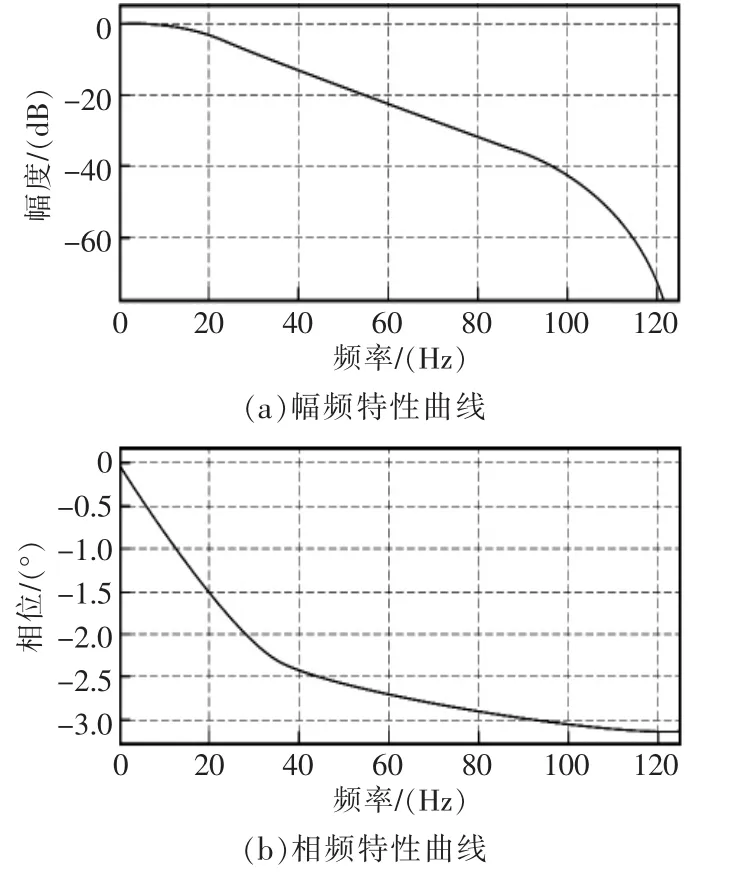
图5 低通滤波器幅频和相频特性Fig.5 Amplitude-frequency and phase-frequency characteristics of low-pass filters

为验证改进型显性互补滤波算法的实时性和准确性，进行了2组试验：第1组为静态试验，测试算法的精确度和静态性能；第2组为动态试验，测试算法在不同角速度下的实时性和动态性能。

当试验平台静止时，分别用标准型显性互补滤波算法和改进型互补滤波ECF算法，解算出四旋翼飞行器的姿态，并记录横滚角和俯仰角（如图6所示）。由图可见，静态测试标准ECF算法中横滚角和俯仰角的波动范围为-0.1～0.1；改进ECF算法中横滚角和俯仰角的波动范围为-0.1～0.1。

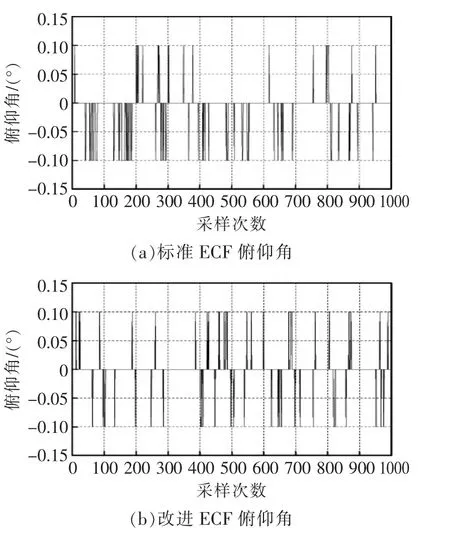
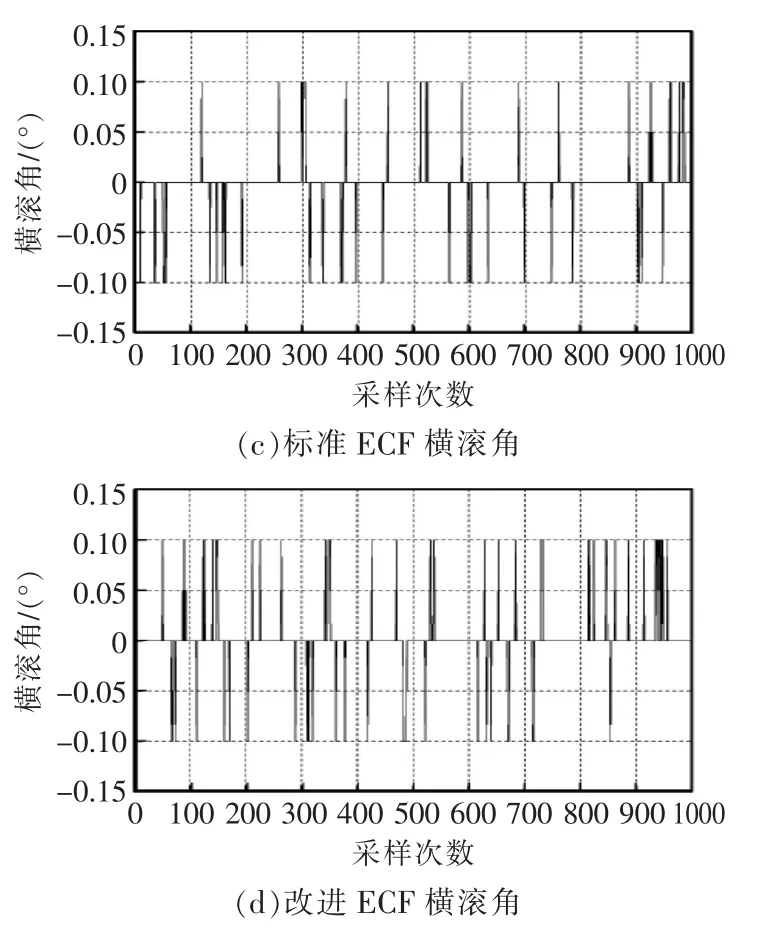
图6 标准ECF和改进ECF静态测试Fig.6 Standard ECF and improved ECF static test

表2给出了2种算法姿态角的均方根误差、最大值及最小值。对比2组数据，可知2种算法在姿态解算的精度上差别不大，说明改进ECF保证了姿态解算的准确性。

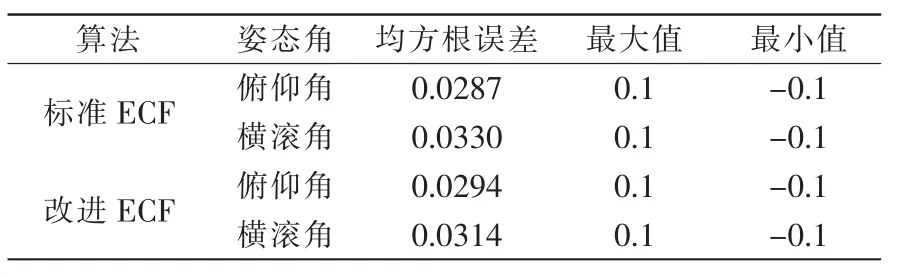
表2 静态测试下两种算法姿态解算误差Tab.2 Attitude estimation errors of two algorithms in static test

将试验平台沿Y轴固定在碳纤维杆上，保证四旋翼只能绕单轴运动。使四旋翼以不同角速度做绕轴运动，同时将2种算法解算出的俯仰角发送至上位机进行显示，姿态采样时间为4 ms；为了更容易观察波形，选取发送周期为姿态采样周期的3倍，如图7所示共选取了1000个采样点。

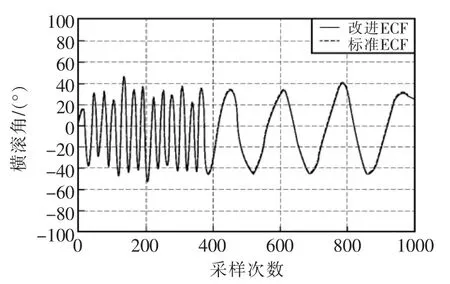
图7 动态测试姿态的整体对比Fig.7 Overall comparison of dynamic attitude testing

为了更清楚地反映不同角速度下2种算法姿态的效果，进行了局部姿态的对比，如图8所示。由图可见，在慢速转动时，2种算法解算的姿态跟随几乎没有差别；而在快速转动时，标准ECF相对于改进ECF解算的姿态有明显的滞后。

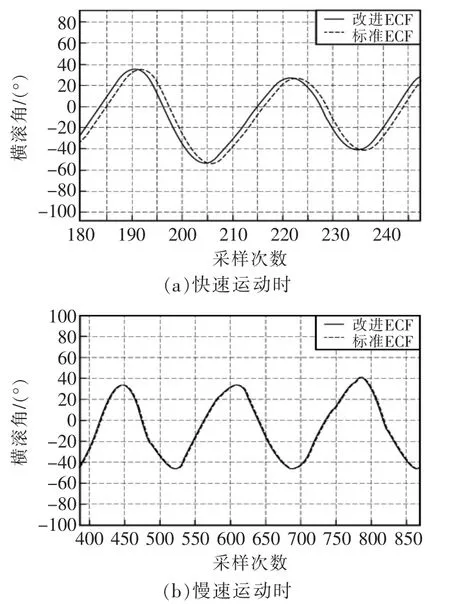
图8 不同角速度运动的局部姿态对比Fig.8 Local attitude comparison of different angular velocities

为了进一步确定标准ECF相对于改进ECF的滞后时间，分别选取在50，150，250，350采样点附近进行比较，对比结果见表3。由表可算出平均滞后时间约为24 ms。

通过动态绕轴试验，说明了改进ECF姿态解算的实时性相对于标准ECF，有了明显的提高。

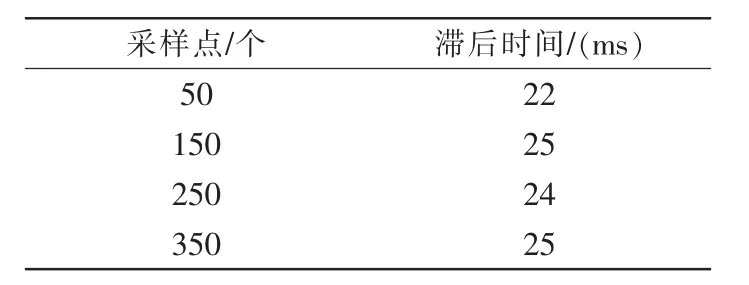
表3 姿态估计滞后时间的对比Tab.3 Comparison of lag time in attitude estimation

6 结语

文中设计了一种改进显性互补滤波算法，在IMU数据融合之前对加速度原始数据进行巴特沃斯低通滤波，同时设置了缓存区保存更新后的四元数向量，在缓存区中取出与加速度对应时刻的四元数向量进行数据融合，在保证了精确度的基础上提高了姿态解算的实时性。为了验证文中所设计算法的有效性和实用性，搭建了四旋翼飞行器试验测试平台，将文中所设计的算法与传统的显性互补滤波算法在试验平台上进行了静态试验和动态绕轴试验。试验结果表明，该算法能有效地减小加速度白噪声对姿态解算精度的影响，改善了加速度低通滤波之后造成姿态解算滞后问题，保证了姿态解算的精确度，提高了姿态解算的实时性。