碳纤维角联织机网络控制系统H∞状态观测器设计

行超琦 ，刘 薇 ，2，周国庆 ，2，吴晓宇

（1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学 天津市现代机电装备技术重点实验室，天津 300387）

由于通信网络，计算机科学和控制领域的多学科性质，网络控制系统NCS已引起学术界和工业界的强烈关注[1]。由于通信或能量限制等原因，信号可能会产生延迟，通信信道中的网络诱导时延严重影响闭环网络控制系统的性能[2]。受系统中通信网络所采用媒体访问控制协议的影响，网络诱导时延将呈现固定、随机时变或不确定时变的特征[3]。针对不同类型的时延，系统需采用不同的分析设计方法[4-7]。

文献[8]研究了已知定常时延对系统建模与控制的影响，设计了最优控制器，然而时延在本质上却是随机的。文献[9]利用信息接收缓冲区，将不确定长时延转变为可以在几个确定的时延之间选择，然而缓冲区的引入导致了时延转化为最大时延，人为的增大了时延，通过牺牲系统的灵敏度来换取控制器对时延变化的鲁棒性。文献[10]研究了针对不确定时延的状态反馈控制器的问题，但是并没有考虑到被控对象的状态不可测的情况。

碳纤维角联织机以碳纤维多层织造技术为基础，与传统织机有着很大的不同[11]。研究碳纤维角联织机网络控制系统问题，目前尚未在已有文献中发现该方面的研究。将网络化控制技术应用到碳纤维角联织机张力控制系统中，使系统具有更好的可靠性。本文针对时延小于等于一个采样周期的情况，设计了一种H∞状态观测器，用于解决碳纤维角联织机张力控制系统中部分状态不可测的问题。仿真结果表明，所设计状态观测器可以快速跟踪实际系统的状态变化，并具有较强鲁棒性。

1 NCS问题描述和模型

状态反馈NCS的结构如图1所示。

图1 状态反馈NCS结构Fig.1 State feedback NCS structure

图中，u为被控对象的输入，y为被控对象的输出，τsc为数据从传感器经网络传送到控制器的时延，τca为数据从控制器经网络传送到执行器的时延。各节点采集、计算、处理数据所花费的时间称为设备时延，若采用的处理器速度足够快，其与τsc和τca相比很小，可忽略不计。假设第k个采样周期从传感器到控制器的网络诱导时延为τksc，从控制器到执行器的网络诱导时延为τkca，为方便分析，作出如下合理的假设。

1）传感器以周期T定时采样，并且通过网络发送给控制器，在测量数据的传输过程中，不存在数据包的时序错乱和丢失；

2）控制器采用高速计算机，一旦接收到来自传感器的数据，立刻进行控制计算，并且将计算得到的控制信号经过网络发送给执行器，计算控制信号的时间忽略不计；

3）执行器一旦接收到控制信号，立刻驱动被控对象来执行相应操作；

4）整个闭环回路的网络诱导时延是不确定的，但其大小不超过一个采样周期，即满足τ∈［0，T］，其中 τk=τksc+τkca；

5）不考虑过程干扰和测量噪声。

基于以上假设，被控对象模型为

式中：x（t）∈Rn，u（t）∈Rr和 y（t）∈Rm分别表示被控对象的状态、控制输入和输出；A，B和C是具有相应维数的常矩阵。

由假设条件可知，被控对象的输入u（t）可以表述为

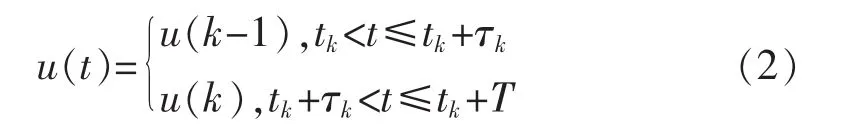
所以，被控对象的离散化模型可以表示为

式中：Ad=eAT，B0，B1，D 和 E 为常矩阵，F（τk）随 τk变化，且满足 FT（τk）F（τk）≤I。

当A含有n个不为零的互异特征根λ1，…，λn时，相应的特征向量矩阵为 Λ=［Λ1，…，Λn］，则有

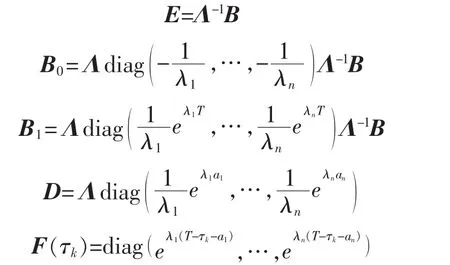
式中：a1，…，an的选取要保证 eλi（T-τk-ai）＜1，i=1，…，n。

令 S（k）=DF（τk）E，表示由不确定时延 τk引起的不确定项，式（3）可写为

假设 Ad非奇异，（Ad，C）能观测，被控对象的状态观测器采用如下模型[12]：

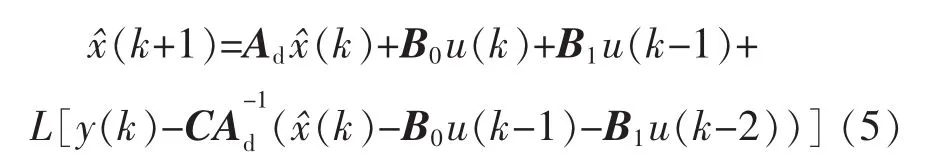
其结构框图如图2所示。

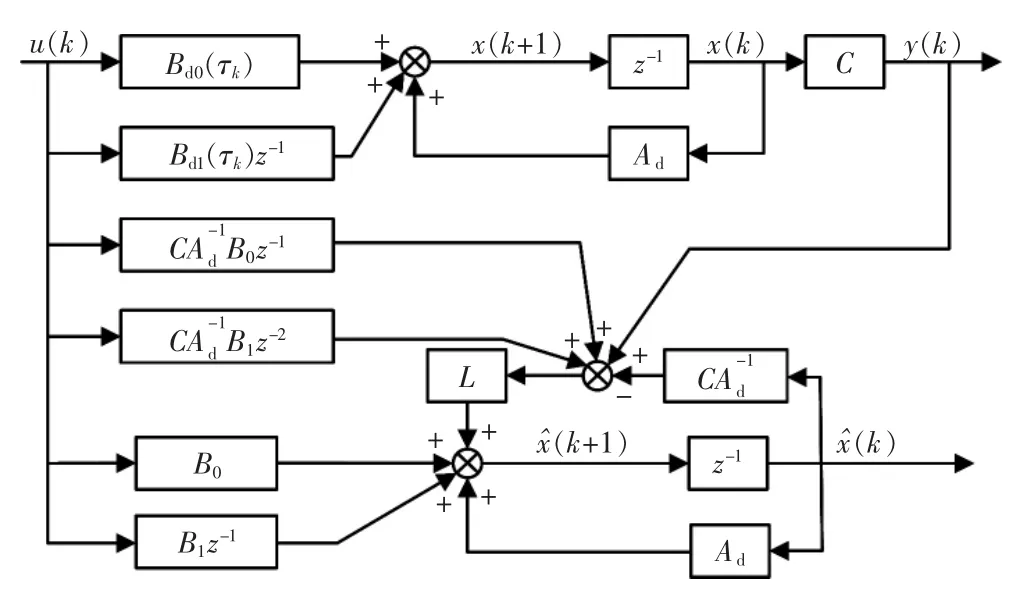
图2 状态观测器结构Fig.2 State observer structure

由于系统网络诱导时延 τk∈［0，T］的影响，k 时刻传输到观测器的信号为

由式（4）可得：

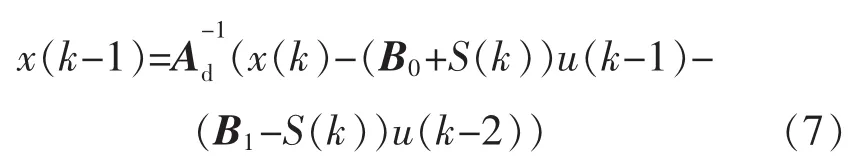
将式（6）和式（7）代入到式（5）中，得到观测器方程为

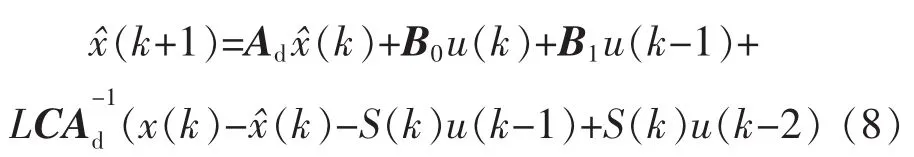
定义估计误差为

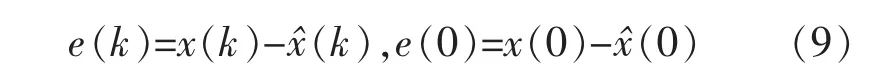
则估计误差方程为

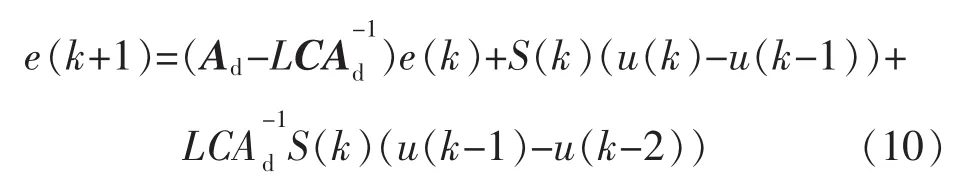
由于 u（k）和 u（k-1）均为已知，则式（10）可以表示为

其中，

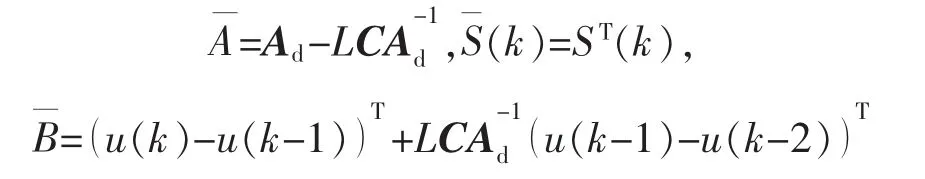
2 H∞状态观测器设计

定义观测器的输出残差方程为

其中，G为加权矩阵。

状态观测器的估计输出误差方程不仅要求渐近稳定，而且还要求观测器的输出能快速的跟踪系统实际的状态变化，而且，由不确定时延所引起的不确定项对观测器状态的估计误差所产生的影响应当尽可能的小，于是，给出如下定义：

定义1如果存在观测器增益L，使得在不考虑时延的影响时，观测器的输出误差渐近稳定；当考虑时延的影响时，在零初始条件（e（0）=0）下，对于给定正常数γ>0，由时延所引起的不确定项和观测器残差 r（k）之间满足 H∞范数约束条件，则状态观测器（5）称为 H∞状态观测器。

定理1当考虑时延影响时，对于给定的正常数γ，如果存在对称正定矩阵Q，矩阵T和X，满足以下条件：

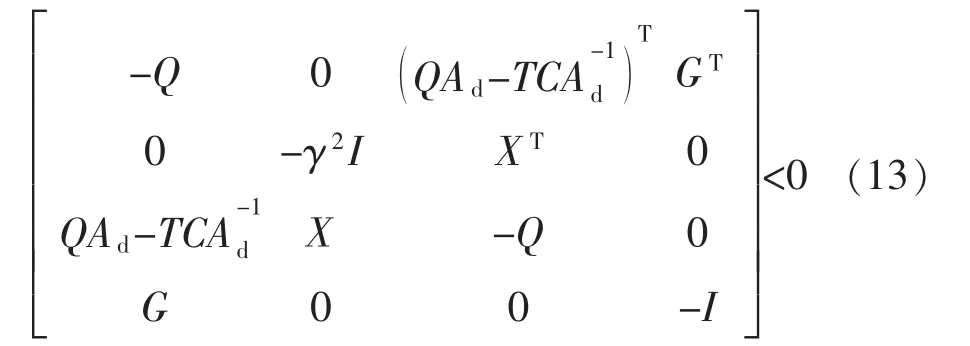
证明 令

对于式（11），选取 Lyapunov函数为

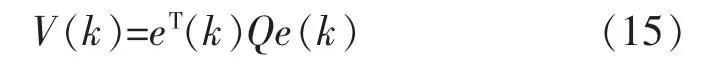
由定理1可知，观测器的输出误差是渐近稳定的。 在零初始条件下，对于，有：

考虑系统式（11），有：

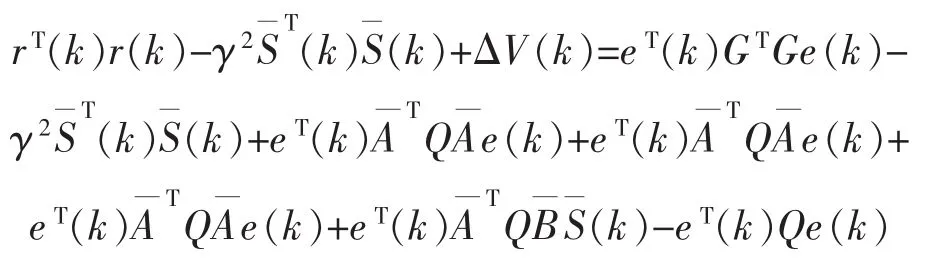
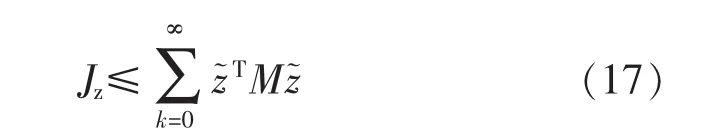
其中：

若使 Jz≤0，需有 M＜0，即有：

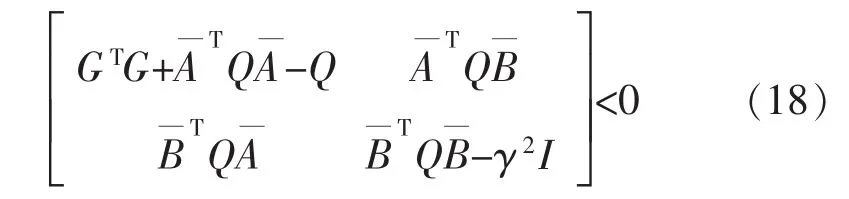
式（18）可写为

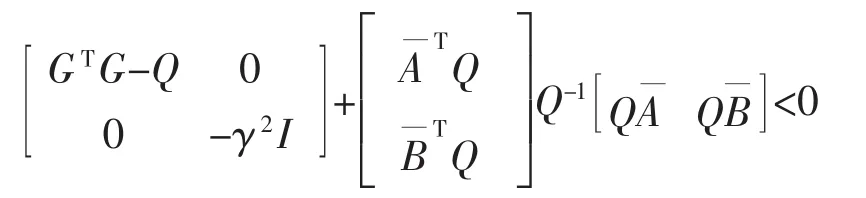
由Schur补性质，上式等价于：

令 T=QL，式（20）等价于式（13）。

证毕。

如果式（13）的条件成立，通过求出可行解Q和T，即可得到观测器的增益参数。

3 基于观测器的NCS鲁棒稳定性

基于之前所设计的状态观测器，将观测器的输出估计状态当作状态反馈控制器的输入，从而实现全状态反馈。

反馈控制器采用如下的无记忆模型：

联立式（9），式（10）和式（21），记 F=F（τk），则估计误差方程为

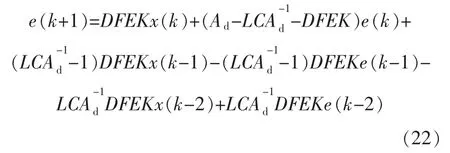
联立式（3），式（9）和式（21），则基于观测器的闭环NCS模型为

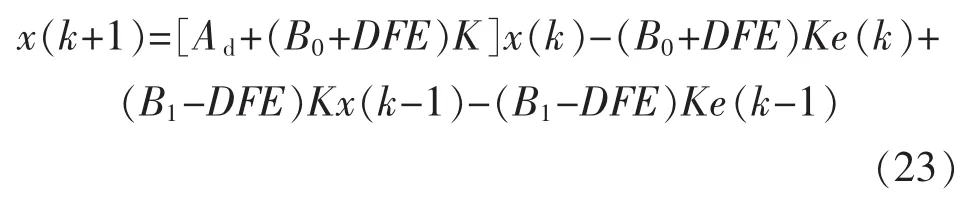
记：

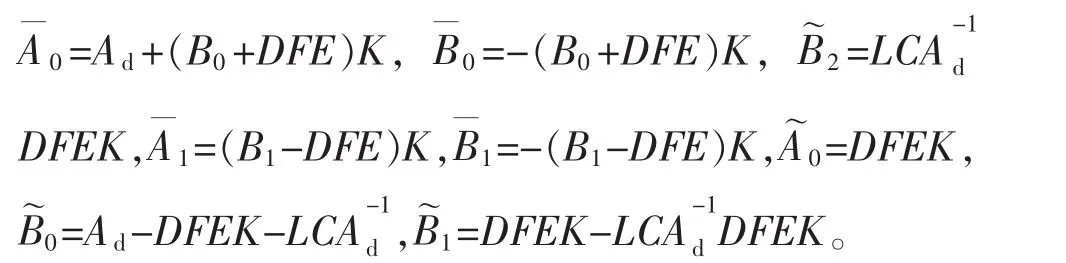
则基于状态观测器的闭环NCS模型为

定理2对于基于状态观测器的NCS（24），如果存在正定矩阵 Pn，n=1，2，…6 和标量 εi（i=1，…4）＞0，满足以下的条件：

证明证明过程参考文献[13]，详细证明限于篇幅略去。证毕。

4 碳纤维角联织机系统中的应用

碳纤维角联织机采用了一种全新的设计，在机构设计和织造工艺动作要求方面比传统织机更为复杂，而且还解决了诸如多层织物逐层引纬一次成型等相关技术难题[14]。

织机主要由送经、开口、引纬、打纬和卷取五大核心装置组成，为了满足不同需求，在各个机构设计上采取了不同的形式，如图3所示。送经部分由主动送经机构、主动摆辊式张力调节结构及拢纱部件组成，送经机构包含60个小经轴和伺服电机，通过设置相对独立的60套送经装置实现对每一层纱线的独立控制；开口机构采用电子提花加多臂复合开口机构；为了提高入纬率，引纬机构采用双向变截面双剑杆引纬机构；为了实现垂直打纬，打纬机构采用四连杆加曲柄滑块机构；卷取机构则采用卷绕式和牵引式多功能卷取机构。

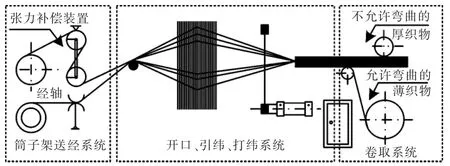
图3 碳纤维角联织机原理示意Fig.3 Carbon fiber multilayer diagonal loom schematic diagram

碳纤维角联织机经纱的起始位置是送经装置，如图4所示，在纱线织造过程中，由于送经机构、开口机构和卷取机构等工艺要求，经常会导致经纱的张力发生变化，因此可以通过控制经纱送经装置的主轴转速来实现系统中张力相对的稳定，而送经系统的传动机构通常是由伺服电机构成，并采用多级减速方案，本文研究的送经系统第一级采用行星齿轮减速器，由蜗轮蜗杆减速箱构成第二级传动机构，最终由涡轮带动主轴实现送经功能。

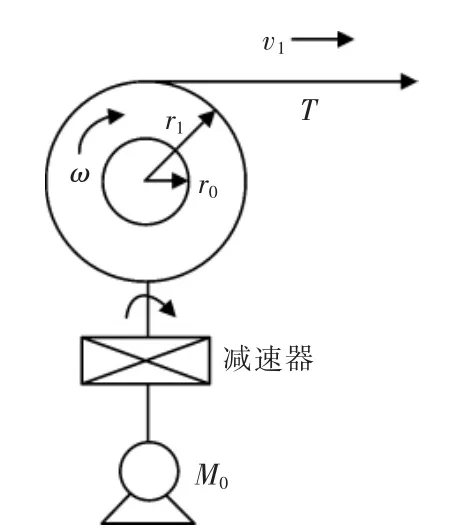
图4 送经机构传动原理示意Fig.4 Schematic diagram of transmission mechanism of let off mechanism

图中T为碳纤维经纱张力，r1为经轴半径，r0为空轴半径，M0为电机电磁转矩，v1为送经线速度；ω为经轴角速度。

对送经主轴进行受力分析，得到送经主轴的运动学方程为

式中：Ms为摩擦转矩；MT为经纱张力矩；Jz为经轴转动惯量；i为传动比。

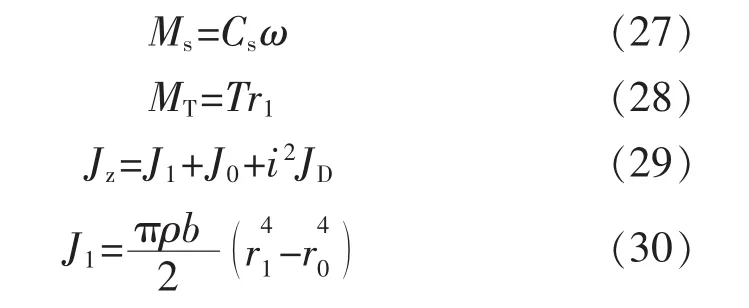
式中：Cs为经轴的粘滞摩擦系数；J0为空轴转动惯量；J1为经纱转动惯量；JD为电机转动惯量；ρ为经纱的质量密度；b为织轴的卷绕宽度。

设纱线卷取的线速度为v2，纱线的张力系数为Kf，则经纱的张力T可表示为

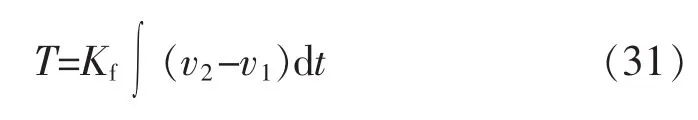
其中：

联立式（26）～式（32），推导出理想状况下送经过程的数学模型为

可以看出，织机的送经系统数学模型是以电机电磁转矩M0为输入控制量，纱线张力T为输出被控量的二阶线性系统。令得到系统的状态方程为

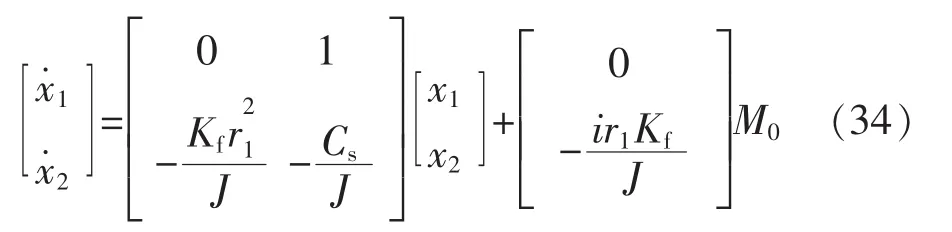
输出方程为

令 u（t）=M0（t），y（t）=T（t），并将参数取值代入得：

取采样周期T=10 ms，并假设网络中的信息传输时延 τk∈［0，T］，且是时变的。A 的特征值为λ1=-0.04，λ2=-0.05，对应的特征向量选取 Λ=，则有

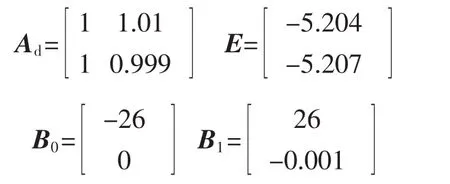
为了保证 eλi（T-τk-ai）＜1，i=1，2，选取 a1=0，a2=-1，则有

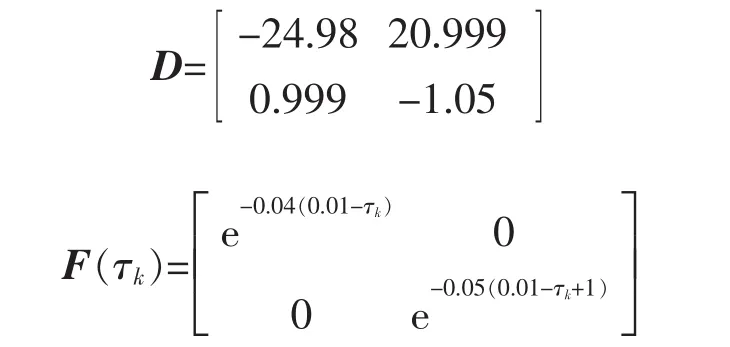
因为 Ad非奇异，（Ad，C）能观测，所以观测器存在条件满足。取其残差加权阵G=C，根据定理1，对于给定常数γ=0.8，利用Matlab的LMI工具箱，调用feasp求解器进行可行性分析，得到可行解分别为

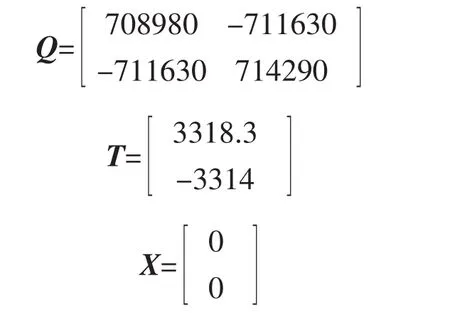
因此，得到H∞状态观测器增益为

反馈控制器增益为

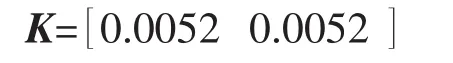
根据定理2，利用同样的方法得到可行解分别为

所以，系统是鲁棒渐近稳定的。

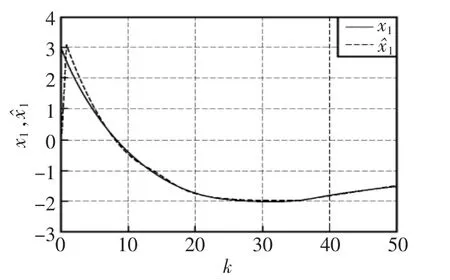
图5 状态x 1及其估计Fig.5 Statex 1 and its estimate

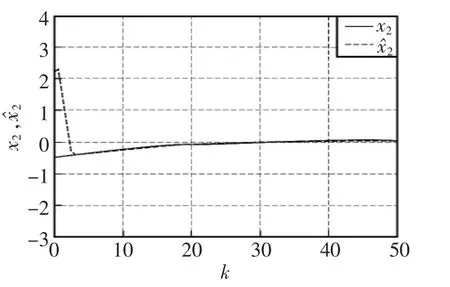
图6 状态x2及其估计Fig.6 State x2and its estimate

由图5和图6可以看出，所设计的状态观测器输出能快速地跟踪系统状态的实际变化，并且使不确定时延所引起的观测器状态估计误差总局限在很小的范围内，表现出良好的鲁棒性和准确性。

5 结语

不考虑系统的测量噪声和过程干扰，在传感器采用时钟驱动、控制器和执行器采用事件驱动、数据包单包传输并且没有数据包丢失的情况下，本文将含有不确定时延的状态反馈网络控制系统建模为具有不确定性的离散时变系统，研究了H∞状态观测器的设计并验证了基于状态观测器的NCS的鲁棒稳定性问题。

运用以上方法，并与碳纤维角联织机相结合，设计出可用于织机的H∞状态观测器。仿真结果表明，所设计状态观测器可快速准确的跟踪系统状态，所以本文所设计的状态观测器是有效可行的。