基于主动学习先验的半监督K-means聚类算法

柴变芳，吕 峰，李文斌，王 垚

(河北地质大学 信息工程学院，石家庄 050031)(*通信作者电子邮箱25304189@qq.com)

0 引言

当前信息社会产生大量数据，聚类技术可以帮助人们快速发现这些数据的类别，进而引用于决策, 有些时候可以很容易标记少量先验信息，提高聚类算法的性能。先验信息主要有两类：第一类是标记的样本类别；第二类是标记的成对约束集合，一对样本属于一类则为must-link，否则为cannot-link。标记样本相当于已知数据的特征和类数，但有些时候很难获得数据的类数，因此，基于两个样本是否属于一类的先验信息往往更易于获得。例如对微博用户的聚类，可通过一些用户发表信息及交互记录判断他们是否属于一类，甚至数据分析师可标定某些用户的类别。半监督聚类技术可将这些先验信息与聚类目标结合，更有效地指导数据的聚类。研究表明，高质量的先验信息不仅可以指导未标注样本进行正确聚类，提高聚类结果的准确性还可以加快聚类的收敛速度[1-4], 因此，设计主动半监督聚类算法是一个值得研究的关键问题。

研究者提出了一些半监督聚类算法，基于先验信息的类别及使用方式分为3类[5]：1)基于距离的半监督聚类算法，这类算法利用成对约束来学习距离度量从而改变样本间的距离，便于聚类。2)基于约束的半监督聚类[6-8], 这类算法使用must-link和cannot-link成对约束关系指导聚类过程。Basu等[6]在K-means算法的基础上引入了must-link和cannot-link成对约束集合作为先验信息，提出了半监督聚类算法PCK-means(Pairwise ConstrainedK-means),提高了K-means聚类算法的性能。3)基于约束与距离的半监督聚类算法, 这类算法实际上是对上述两种算法的总结。Basu等[9]提出了一个基于隐马尔可夫随机场(Hidden Markov Random Field, HMRF)的半监督聚类的概率模型，该模型概括了先前将约束与欧氏距离相结合的方法，并在此基础上提出了一种分区半监督聚类算法，最后通过实验验证了算法的性能。

半监督聚类效果经常受随机选择得到的先验信息的影响，为得到更好的聚类效果，主动半监督聚类将主动学习与半监督聚类相结合，通过一定的选择策略主动选择未标注数据进行标注。Basu等[6]在PCK-means算法的工作基础上，采用最远距离优先策略，通过Explore和Consolidate两个阶段主动选择样本点，在给定的查询次数内构建并扩充成对约束集合，提出了主动半监督聚类算法APCK-means(Active Pairwise ConstrainedK-means)，进一步提高了算法的准确性，但是该算法对于离群点和噪声点过于敏感。Xiong等[10]提出了一种基于迭代的主动半监督聚类框架(Iteration-based Active Semi-Supervised Clustering Framework, IASSCF), 该框架初始随机选择一个节点，然后迭代进行聚类。在每次迭代过程中首先运行半监督聚类，然后根据当前聚类结果主动选择一个最具价值信息的样本点扩充到先验信息集合。选择的样本点不确定性高，且确定该未标注样本点与已标注样本的约束关系所需的查询次数尽可能少。IASSCF框架可基于约束先验实现半监督聚类，并且能主动选择信息量大的样本去标注，聚类准确性高；但是其随机选择的初始先验信息较少，导致迭代初期聚类效果不佳，进而影响后续聚类结果，此外，每次迭代只选择信息量最大的一个点标记，导致运行速度慢、性能提升较慢。

针对此问题，本文设计一种基于主动学习先验的半监督K-means聚类算法——IASSCF_PCK-means，该算法基于主动选取聚类初始中心的思想[11]，选取部分代表性较高的样本点，查询其之间的成对约束关系，构建初始先验节点集合，将构建好的初始先验节点集合作为IASSCF框架的初始先验信息，用以解决在迭代初期先验信息过少导致最终聚类结果效果不佳的问题；同时，将原IASSCF框架中每次迭代过程仅选择一个最具有价值信息的样本点改进为基于当前聚类结果为每一簇选择一个最具价值信息的样本，减少迭代次数，加快算法运行速度，提高算法性能。最后在UCI数据集[12]上验证IASSCF_PCK-means算法的有效性。

1 本文算法IASSCF_PCK-means

带有初始先验节点集合的迭代式主动半监督聚类包括构建初始先验节点集合和基于重要性多节点的主动半监督聚类两部分。首先构建包含多个样本点的初始先验节点集合作为先验信息；然后指导迭代式聚类过程，并且在迭代过程中通过主动选择策略选择多个价值信息较大的无标记样本加入到先验信息集合，指导后续聚类。

1.1 构建初始先验节点集合

从数据集中选择若干代表性较高的点，查询这些点之间的约束关系(must-link或cannot-link)，构建初始先验节点集合。

定义1 若两个样本点满足must-link约束关系，则这两个样本必须被指派到同一簇中；若这两个样本满足cannot-link约束关系，则这两个样本点必须被指派到不同的簇中。

代表性较高的点需同时满足以下两个特点：

1)本身的密度大且其周围样本点的密度均不超过它；

2)与其他密度更大的样本点的距离较远。

样本点密度的计算公式如下：

(1)

其中

(2)

参数dc>0为截断距离，通过计算数据集D中不同样本两两之间距离并按升序排序，然后由用户设定一个百分比参数，dc为该排列的参数百分比上的数。后文实验中设定的百分比参数为2%。

由以上可知，样本xi的密度ρi表示数据集D中除xi外的其他样本点与xi的距离小于dc的样本个数。

如果xi不是样本集D中密度最大的样本点，则xi与其他密度高于自身的样本点之间的距离δi的计算公式为：

(3)

如果xi是样本集D中密度最大的样本点，则:

(4)

至此，可求得数据集D中每个样本点的ρ和δ值，将D中的样本点按照ρ·δ的值从大到小排序，则排序越靠前越具有代表性。查询前几个样本的约束关系，构建初始先验节点集合N={N1,N2,…,Nl}，其中l≤k,k为聚类的簇个数。构建初始先验节点集合的算法在算法1中给出，初始先验节点集合中的样本点满足如下关系：

1) 若xi与xj均属于Np，则xi与xj有must-link约束关系。

2) 若xi属于Np，xj属于Nq，且p≠q, 则xi与xj满足cannot-link约束关系。

算法1 initNeighborhoods(D,k,T,C)。

输入 数据集D，指定选择代表性高的样本点个数k，给定查询次数T，约束集合C=∅;

输出 邻域集合N，剩余查询次数Tleft,约束集C。

1)

t=0，l=1

2)

计算截断距离dc；

3)

计算D中所有样本点的ρ值；

4)

计算D中所有样本点的δ值；

5)

将所有样本点的ρ值与δ值对应相乘，并按照从大到小的顺序排序，并取排序后的前k个样本，得到reprePoints[1..k];

6)

N1={reprePoint[1]}

7)

forj=2 tok

8)

for 每个Ni∈N

9)

t++;

10)

查询reprePoints[j]与所有xi∈Ni的约束关系。如果reprePoints[j]与xi满足must-link约束，则Ni=Ni∪{reprePoints[j]}并更新约束集合C,否则，break；

11)

end for

12)

如果reprePoints[j]与N中所有样本点均不满足must-link约束，则l++；Nl= {reprePoints[j]}; N=N∪Nl

13) end for

14)

Return N;Tleft=T-t;C

1.2 基于重要性多节点的主动选择策略

IASSCF中每次迭代都进行一次半监督聚类，并且依据当前聚类结果主动选择一个最有价值的样本点，查询其与已标注样本点的信息，将其加入到先验信息集合, 该方法可以高效地扩充先验信息集合，但是每次迭代仅选择一个样本点，导致迭代次数过多，算法运行过慢。基于其不确定性度量方法，改进主动选择策略：在每次迭代过程中针对每一簇选择一个价值信息率最大的样本点扩充到先验信息集合。主动选择样本点的方法基于以下假设：对不确定性越大的样本进行标注带给聚类结果的收益很显著，相反，对于所属簇较为明晰的样本进行标注所带来的收益微乎其微；同时，对于不确定性越大的样本，对其进行标注所消耗的查询次数花销越大, 因此，要在不确定性和花销之间权衡，即在给定的查询次数内尽可能多地选择不确定性大的样本扩充到先验节点集合，提高聚类性能。

主动选择策略中选取最有价值的样本点基于以下两个指标：不确定性和查询开销的期望。这两个指标均是在执行完一次聚类后，在其聚类结果的基础上计算。π表示当前数据集的聚类结果，π(xi)表示样本xi当前被指派的簇标记。

1)不确定性度量通过以下几个步骤完成: 首先，使用留出法将带有类标记的数据集划分成训练集和测试集，使用训练集训练出带有50棵决策树的随机森林; 将数据集D中所有样本两两一组使用随机森林进行分类，统计随机森林中将该对样本划分为一类的决策树个数，统计出的决策树个数除以随机森林包含的决策树总个数即为该对样本的相似性; 计算完成后，得到样本间相似度矩阵M，其中M为m×m维的矩阵，m为数据集D中的样本个数，M(i,j)表示样本xi和样本xj的相似度； 然后，在样本间相似度矩阵M的基础上通过计算样本x和Ni中所有样本相似度的平均值作为x和Ni的相似度，归一化求得样本x属于Ni的概率值p(x∈Ni)，计算公式如下：

(5)

其中：|Ni|表示邻域Ni中样本的个数，l表示邻域集合N的元素个数。最后，计算样本x属于各个邻域概率的熵值作为其不确定性度量指标，H(N|x)的计算公式如下：

(6)

2)查询开销的期望是基于式(5)的计算结果。通过式(5)已求得样本x属于邻域集合N中各个邻域的概率, 由于给定查询次数有限，因此应力求消耗更少的查询次数来确定x与各个邻域的关系。通过式(5)的计算结果的值按照降序将各个邻域重新编号，即排序后满足p(x∈N1)≥p(x∈N2)≥…≥p(x∈Nl)。q(x)表示确定x与邻域的所属关系所用到的查询次数，则p(q(x)=i)=p(x∈Ni)。查询次数q(x)的期望值可表示为：

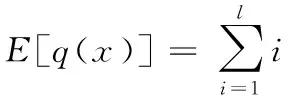
*p(x∈Ni)

(7)

将不确定性越大的样本扩充到先验节点集合，对算法结果带来的收益越大，但是对不确定性大的样本进行标注往往开销很大，因此，应综合考虑不确定性与查询开销，即不确定性尽可能大的同时查询开销尽可能少，可通过式(8)得到基于当前指派结果π的每个簇中性价比最高的样本点。

(8)

其中u表示不在邻域集合中的其他样本集合。主动选择策略在算法2中给出。

算法2 MostInformative(D,π,N)。

输入 数据集D，当前聚类指派结果π，邻域集合N={N1,N2,…,Nl};

输出 选定的样本集合X。

1)

根据当前聚类指派结果训练随机森林，并求得样本间相似度矩阵M

2)

for 每个x∈D，且x∉N

3)

fori=1 tol

4)

通过式(5)计算p(x∈Ni)

5)

end for

6)

通过式(6)计算H(N|x)

7)

通过式(7)计算E[q(x)]

8)

end for

9)

通过式(8)计算X

10)

ReturnX

1.3 算法描述

IASSCF中从数据集D中随机选取一个样本点作为先验节点，加入到邻域集合中，然后开始迭代。每次迭代以邻域集合作为先验信息进行一次半监督聚类，并根据当前聚类结果主动选择一个最有价值的点，查询该点与邻域集合中各个邻域中样本点的关系，将该点加入到先验节点集合，指导下一次半监督聚类，直到查询次数达到给定查询次数。

IASSCF的初始先验节点集合中的样本为随机选择。在迭代次数较少时由于先验信息过少可能导致聚类准确率不高。IASSCF通过主动选择策略选择的样本很大程度上依赖于上一次的聚类结果，因此，迭代初期聚类效果不好会直接导致最终的聚类结果不佳，且在IASSCF框架中每次迭代只选取一个最有价值的点扩充到先验信息集合中，在给定查询次数的前提下，存在先验节点集合扩充过慢、迭代次数过多、算法运行时间过长等问题。鉴于此，使用Rodriguez等[11]提出的选择代表性较高样本的方法构建初始先验节点集合，作为IASSCF框架的初始先验节点集合, 并将IASSCF框架中每次迭代只选择一个样本的主动选择策略改进为每次迭代基于当前指派结果为每一簇选择一个信息价值最大的样本。在以上改进的基础上，本文提出了IASSCF_PCK-means算法。IASSCF_PCK-means的算法流程在算法3中给出。

算法3 IASSCF_PCK-means(D,k,T,C)。

输入 数据集D，聚类个数k，给定查询次数T，成对约束集合C=∅；

输出 聚类结果π。

1)

[N,Tleft,C] = initNeighborhoods(D,k,T,C)

2)

repeat

3)

π= PCK-means(D,k,C)

4)

X= MostInformative(D,π,N)

5)

for 每一个x*∈X

6) 按p(x*∈Ni)从大到小将N中的邻域重新排序

7)

fori=1 tol

8) 查询x*和所有xj∈Ni的约束关系

9)

Tleft--；

10)

如果x*和xj满足must-link约束，则Ni=Ni∪{x*}并更新约束集合C,否则，break；

11)

end for

12)

若x*与N中所有样本点均无must-link约束，则l++;Nl={x*};N=N∪Nl;

13)

end for

14)

untilTleft≤0

15)

Returnπ

算法3中，在步骤1)构建初始先验节点集合N。从步骤2)开始进行迭代，在迭代过程中，步骤3)以成对约束集合C为先验信息，通过PCK-means算法得到聚类结果π。步骤4)通过成对约束集合C和当前聚类结果选择出最有价值信息的点集合X。对于每个x*∈X，在步骤6)将邻域集合N重新排序。步骤7)～12)查询x*与邻域集合N中各个邻域中样本点的约束关系，并将x*加入到邻域集合N中，同时更新成对约束集合C。步骤13)表示达到迭代停止条件即达到最大可查询次数时算法结束。迭代停止后输出最后一次聚类结果即为最终聚类结果。

2 实验与结果分析

以标准互信息(Normalized Mutual Information, NMI)[13]作为评价指标，对比PCK-means算法、结合PCK-means算法和IASSCF框架的主动半监督聚类算法(下文用IASSCF_old表示)以及IASSCF_PCK-means算法的NMI值，测试迭代框架对聚类结果性能的提升以及改进IASSCF框架后的主动半监督K-means算法的性能; 同时，对比两种主动半监督算法的运行时间，测试改进IASSCF框架后的IASSCF_PCK-means算法的效率。

实验中，使用了4组UCI数据集：Iris、Wine、Seeds和Ecoli, 每种数据集的信息如表1所示。针对每个数据集分别给定50、100、150、200、250个可查询次数，NMI值与运行时间均为程序运行10次的平均结果，具有一定的代表性。

表1 实验用数据集信息

图1(a)为三种算法在Iris数据集上的测试结果。横向上，随着给定约束对个数的增加，三种算法得出的聚类结果的NMI值均有不同程度的提升。PCK-means算法NMI值提升较为缓慢，但总体呈上升趋势；IASSCF_PCK-means算法的NMI值提升最为明显，在给定200个约束对时，NMI值已经达到1；IASSCF_old算法在给定200个约束对时NMI值达到峰值，当给定250个约束对时的NMI值不仅没有提升，反而与给100个约束对时的NMI值基本持平，这是因为IASSCF_old算法的初始先验节点为随机选择，在迭代初期的聚类效果不理想，影响了后续迭代，从而导致最终聚类结果的NMI值较低。纵向上，两种基于迭代框架的IASSCF_old算法和IASSCF_PCK-means算法在给定相等的约束对的个数时，NMI值明显高于PCK-means算法，体现出迭代框架的优越性。

图1(b)为三种算法在Wine数据集上的测试结果。同样，可以很明显看出两种基于迭代框架算法在给定相同约束对下聚类结果的NMI值要明显高于PCK-means算法。IASSCF_PCK-means算法随着约束对个数的增加，NMI值一直处于上升趋势；IASSCF_old算法在给定约束对大于等于150个时，NMI值基本持平，在程序运行的10次中有少数几次的聚类结果效果不好导致NMI的平均值较低；与IASSCF_old算法相比，带有初始先验节点集合的IASSCF_PCK-means算法的稳定性更好，NMI值更高。

图1(c)与图1(d)分别为三种算法在Seeds数据集和Ecoli数据集上的结果。图中明显可以看出基于迭代框架的两个算法IASSCF_old和IASSCF_PCK-means的NMI值高于PCK-means算法，且带有初始先验节点集合的算法IASSCF_PCK-means相比IASSCF_old算法更稳定，NMI值更高。

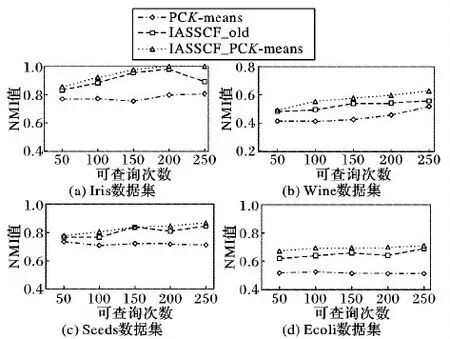
图1 在不同数据集上给定不同查询次数的NMI值

图2为IASSCF_old算法和IASSCF_PCK-means算法在不同数据集上的运行时间对比。IASSCF框架在迭代过程中不断扩充先验节点集合，对数据集进行重新聚类，并且每次选择最具价值信息的样本时都需要训练随机森林、计算样本间的相似度矩阵等大量的计算过程； IASSCF_old算法每次迭代主动选择一个最具价值信息的样本扩充到先验节点集合； 而IASSCF_PCK-means算法在每次迭代主动选择每一簇中最具价值信息的样本将其扩充到先验节点集合。在给定查询次数的前提下，IASSCF_PCK-means算法扩充先验节点集合的速度更快，迭代次数更少，也能够大幅提高算法的效率。从图2的统计图可以看出IASSCF_PCK-means的运行时间约为IASSCF_old的1/k，其中k为聚类个数。

3 结语

基于迭代框架的IASSCF_old算法和IASSCF_PCK-means算法在迭代过程中可以根据上次聚类结果主动选择节点扩充到先验节点集合，并根据先验信息不断调整聚类，在算法性能上要优于PCK-means算法; 并且加入了初始先验节点集合的IASSCF_PCK-means算法在稳定性和NMI值上要更优于IASSCF_old算法，同时，由于在每次迭代中选择多个信息价值较高的样本点，所以在算法效率上，IASSCF_PCK-means算法要比IASSCF_old算法更高。但是，由于IASSCF框架需要大量的计算过程，相较于普通聚类算法执行效率仍然偏低。针对以上问题，下一步工作将围绕以下两方面进行：1)将IASSCF_PCK-means算法迁移到Spark平台，如训练随机森林的过程即可以将训练每一棵决策树放到Spark集群的不同节点上，通过并行计算提高算法执行效率；2)将框架中的半监督聚类算法PCK-means替换为其他软化分聚类方法，通过软化分得到样本属于各个簇的概率，并计算熵值来作为其不确定性度量指标，省去训练随机森林的过程，提高算法效率。

图2 在不同数据集上给定不同查询次数的运行时间