展平化直 巧求最值

■冯睿琦

将空间图形问题转化为平面图形问题,是解决立体几何问题常用的基本方法。在求空间图形表面两点间的最短距离时,常运用“展平变换,化曲(折)为直”,即把“折线拉成直线,曲面展成平面”,从而使问题得以巧妙解决。下面通过对两道典型试题的求解思路进行探索来说明“展平化直”的妙处。

一、多面体的展平化直

例1 如图1,一质点从点A出发,在棱长为a的正方体ABCD-A1B1C1D1的表面运动到点C1,求它经过的最短路线长。

图1

思路探索：①题目给出了正方体的棱长,需要求的是表面上一点到另一点的最短长度,如何来求最短长度?在正方体表面上“转来转去”恐怕很难确定何时长度最短。但将正方体的表面展平,“化折为直”,连接AC1即得最短长度。②求最短路径长度的方法找到了,那么如何去展平正方体的表面呢?展平表面的依据是展开后正方体表面上的线段长度不改变。展开后化异面为共面,可用“两点之间线段最短”确定最短路线的长。从点A到达点C1要经过两个面,共有六条途径,将这些面展平在同一个平面上,可归结为如图2、图3所示的两种情形。通过上述的思路分析,我们就很容易求出最短路线长了。

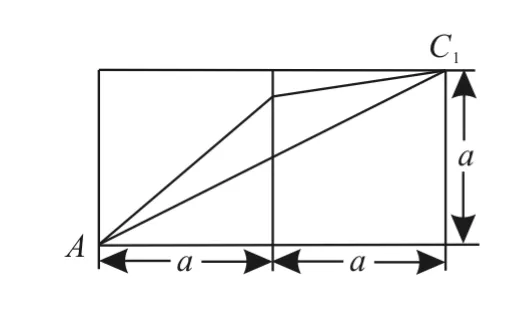
图2

图3

解答过程：将点A到达点C1要经过的两个面展平在同一个平面上,可归结为如图2、图3所示的两种情形。从中我们会发现质点运动的路线一般为两条折线,根据“两点之间线段最短”可知,只有沿线段AC1运动时,路线才最短,易得图2、图3中点A,C1间的最短距离为,即质点经过的最短路线长为。

二、旋转体的展平化直

例2 如图4,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A。

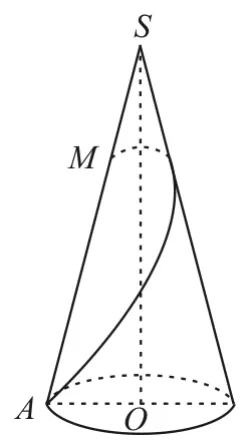
图4

(1)求绳子的最短长度的平方f(x)。

(2)求绳子的最短长度的最小值和最大值。

思路探索：①题目给出的是已知底面半径、母线长的圆锥,需要求的是圆锥侧面上两点A,M间所拉绳子的最短长度(两点间的最短距离),如何来求最短长度?在圆锥侧面上“绕来绕去”恐怕很难确定何时长度最短。如图5,沿母线SA将圆锥的侧面展开,“化曲为直”,连接AM 即为绳子的最短长度。②绳子的最短长度AM找到了,可如何用x表示它的平方呢?由图5可以看出,只好利用△ASM了。在△ASM中,已知SA=l=4,SM=x,关键是求出侧面展开图——扇形的中心角∠ASA"。怎样求出∠ASA"?这可能是许多同学犯难的地方。我们知道,扇形是圆的一部分,圆周角是360°,只要知道扇形所占圆的“份额”,扇形的中心角就能够求出来了。这里,扇形所在的圆以圆锥母线的长SA=l=4为半径,圆周长为C=2πl=8π,扇形的弧长(即圆锥底面圆的周长)为l"=360°=90°。 ③ 求 出 ∠ASA"=90°后,在△ASM中,由勾股定理就可以用x表示出绳子的最短长度AM的平方f(x)了。由于M为母线SA上的一点,且SM=x,所以0≤x≤4。④根据f(x)和x的范围,利用函数知识求出f(x)的最小值和最大值,进而求出绳子的最短长度的最小值和最大值。

解答过程：(1)将圆锥的侧面沿SA展开在平面上,如图5,则该展开图为扇形,且弧AA"的长度l"就是☉O的周长,所以l"=360°=90°。由题意知绳子的最小值为展开图中的AM,故),所以

图5

(2)由(1)知,当x=0时,f(x)min=02+16=16,此时绳子的最短长度的最小值为4;当x=4时,f(x)max=42+16=32,此时绳子的最短长度的最大值为42。

跟踪练习：如图6,在直三棱柱ABCA1B1C1中,AB=BC=BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,求沿棱柱的表面从点E到点F的最短路径的长度。

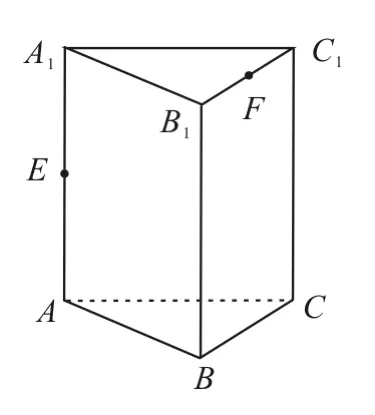
图6

参考答案与提示：将直三棱柱的侧面、底面展开,有如图7所示的三种情形。在图①中,EF=;在图②中,作EG垂直于BB1,垂足为G,;在图③中,过E作AC的平行11线,过F作CC1的平行线,两线交于点H,通过比较可知,点E沿平面AA1C1C过棱A1C1到点F的路径最短,故E,F两点间的最短路径的长度为

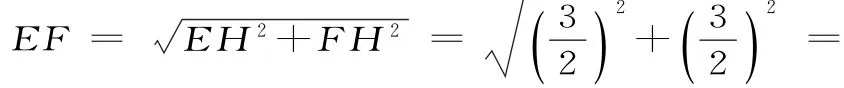
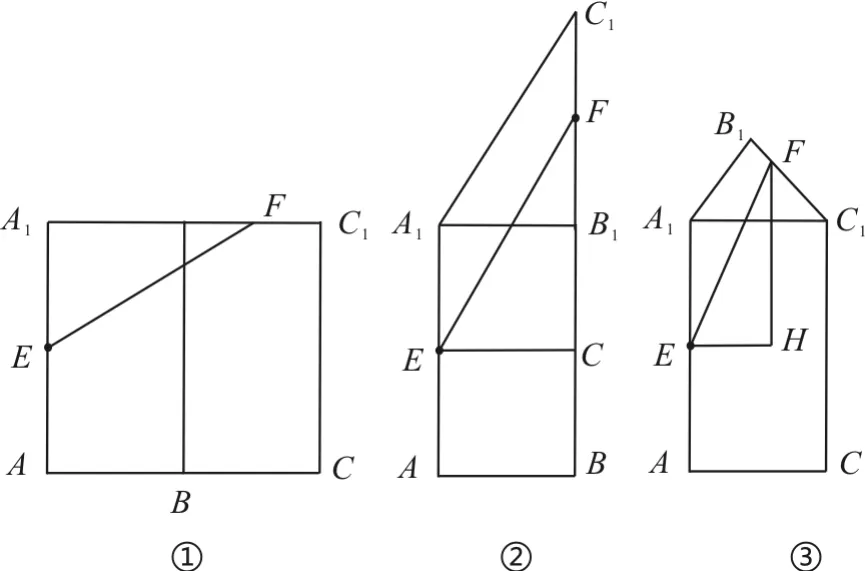
图7