温度对我国近期H7N9型禽流感传播影响的数学分析

张琬婧， 汤琳瑜， 陶益婷， 林支桂

(扬州大学 数学科学学院，江苏 扬州 225002)

2013年3月底开始，在上海和安徽两地出现了禽流感疫情，引起疫情的H7N9型禽流感病毒是首次发现的新亚型流感病毒，当时尚未纳入我国法定传染病监测报告系统，目前也无有效的疫苗进行及时防控。并且初期感染者均出现发热、咳嗽、头痛、肌肉酸痛和全身不适等特征，重症感染者甚至导致死亡，且死亡率高达35%[1]。目前尚未证实此类病毒是否具有人传染人的特性。

由于气候异常等多种因素的影响，全球禽流感疫情呈高发态势，我国的H7N9型禽流感在2013年春季爆发过后，又出现几波较为明显的疫情，整体均呈现出分布广、病例多、传播快等特点，且主要在经济发达的南方地区爆发大规模疫情，进而对我国经济发展和人民生活造成了较大影响。

本文以2013年至2015年爆发的三波禽流感疫情的病例数据为基础，建立模型进行理论分析，利用软件进行模拟，为未来禽流感疫情发展趋势的预测和防控提供定量分析工具[2-6]。

1 经典的Logistic模型

世界卫生组织(WHO)发布了2013年3月27日至2015年3月28日期间中国(包括香港在内)累计确诊H7N9型禽流感病例人数(见：http://www.who.int/mediacentre/factsheets/avian_influenza/zh/)，下面给出三波病例发展趋势图。第一波：2013年3月31日至2013年5月10日(图1按天统计)；第二波：2013年12月19日至2014年3月19日(图2按天统计)；第三波：2014年12月14日至2015年3月28日(图3按周统计)。

图1 第一波禽流感累计发病人数(按天)

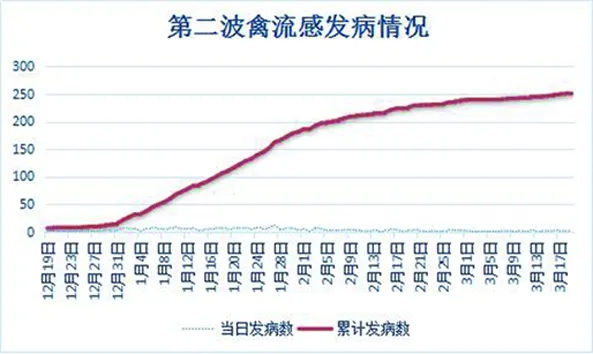
图2 第二波禽流感累计发病人数(按天)

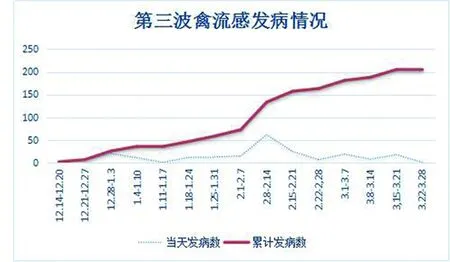
图3 第三波禽流感累计发病人数(按周)Fig.3 The cumulative number of total avian influenza infected cases in China(by week)

首先考虑经典的Logistic增长模型[7-9]

(1)

其中，r为禽流感发病率，k为预防效果指数，N为累计发病人数。对(1)式求解得到

(2)

根据已知的2013年3月27日至2015年3月28日累计发病人数，可以用Matlab软件进行拟合，求出模型的系数，得到拟合曲线，如图4所示。

第一波：k=0.001815,r=0.2336,N0=3,

第二波：k=0.0007038,r=0.16,N0=1,如图5所示。

图4 经典的Logistic曲线；原始数据

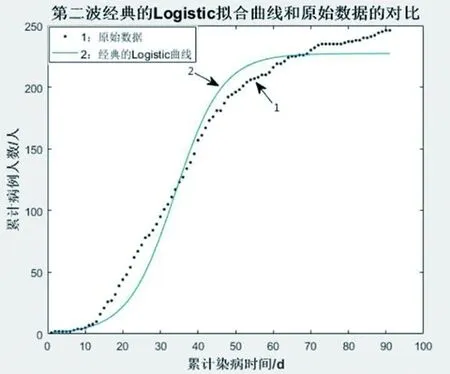
图5 经典的Logistic曲线；原始数据

第三波：k=0.003121,r=0.6335,N0=1,如图6所示。

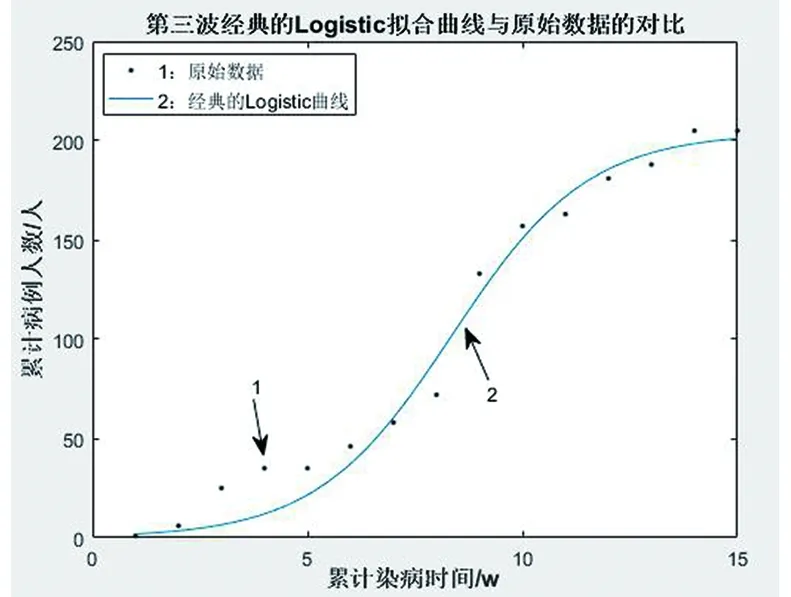
图6 经典的Logistic曲线；原始数据Fig.6 The classical Logistic curve;Raw data.

显然，经典的Logistic模型与实际数据有较大的误差，不能很好地拟合。

2 具温度的Logistic模型

为达到更好的拟合效果，我们将经典的Logistic模型进行改进。由于病毒活性受到温度影响，而当日禽流感发病率的变化与“前几天温度”有关，上述的“前几天”即为传染病的潜伏期。根据世界卫生组织(WHO)的资料，本文视禽流感的潜伏期为7天左右，并且取当日前7天疫情主要地区的平均气温作为禽流感的潜伏期温度。图7，8和9表示了疫情当日前7天的平均温度变化情况(见天气网：http://lishi.tianqi.com/)。

考察潜伏期温度θ(t)对发病增长速率r的影响，改进后的Logistic模型为

(3)

其中，α,β为参数，θ(t)为当时前6，7，8天的平均温度，即潜伏期温度。(3)式化为

N(t+1)-N(t)=(β-αθ(t))N(t)-kN2(t)。

(4)

(4)式为多元线性方程，通过数学软件Matlab的拟合功能可以得出α,β,k的参数估计值，

第一波：α=0.001957，β=0.2353，k=0.001541,如图10所示。

第二波：α=0.00047，β=0.11，k=0.0004,如图11所示。

第三波：α=0.01753，β=0.6521，k=0.002418,如图12所示。

而已了解到病毒会在一个特定的温度下活性最强，该温度我们称之为最适环境温度，最后考虑具最适温度的Logistic模型：

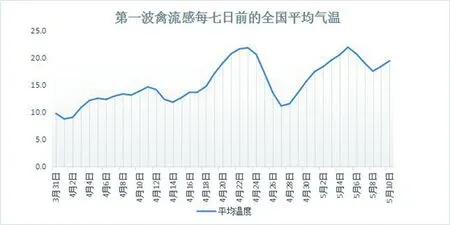
图7

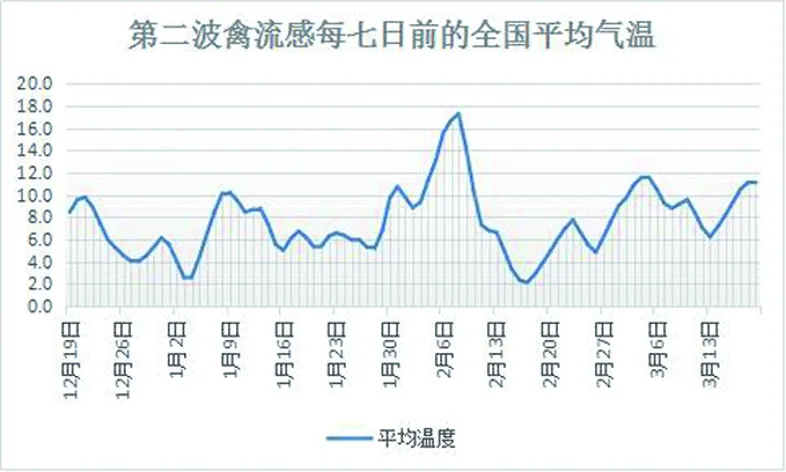
图8

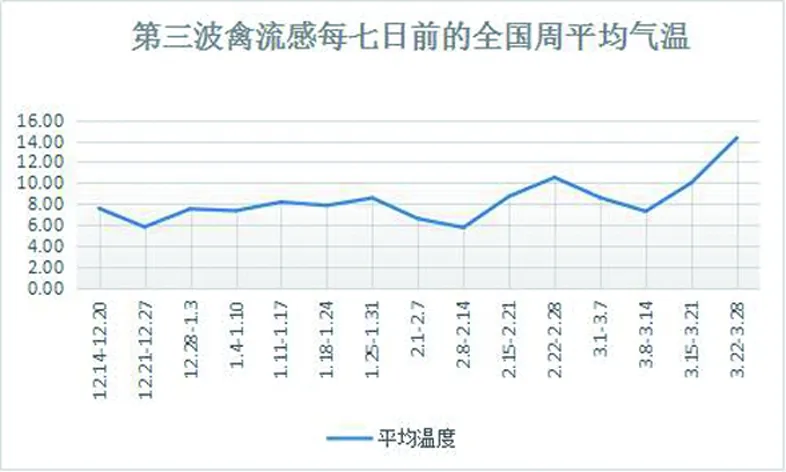
图9 主要地区疫情爆发当日前7天平均温度变化图(按周)

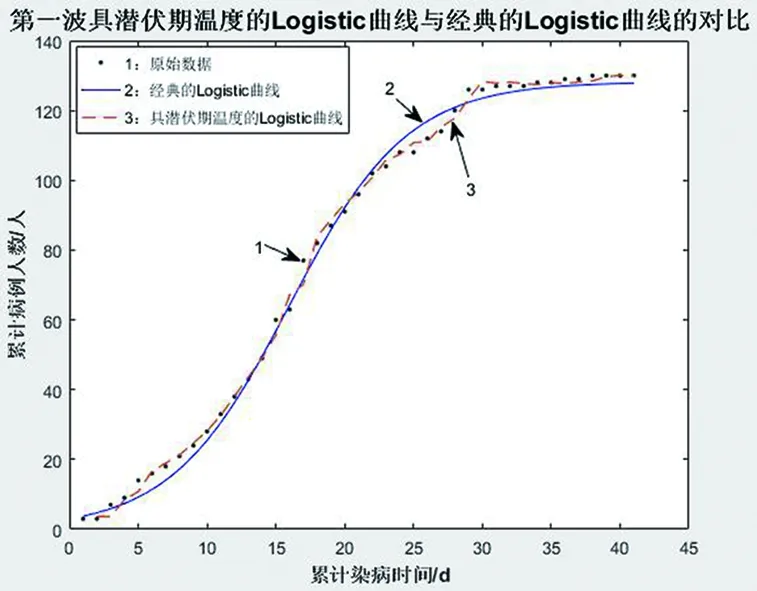
图10 第一波具潜伏期温度的Logistic曲线；原始数据；经典的Logistic曲线

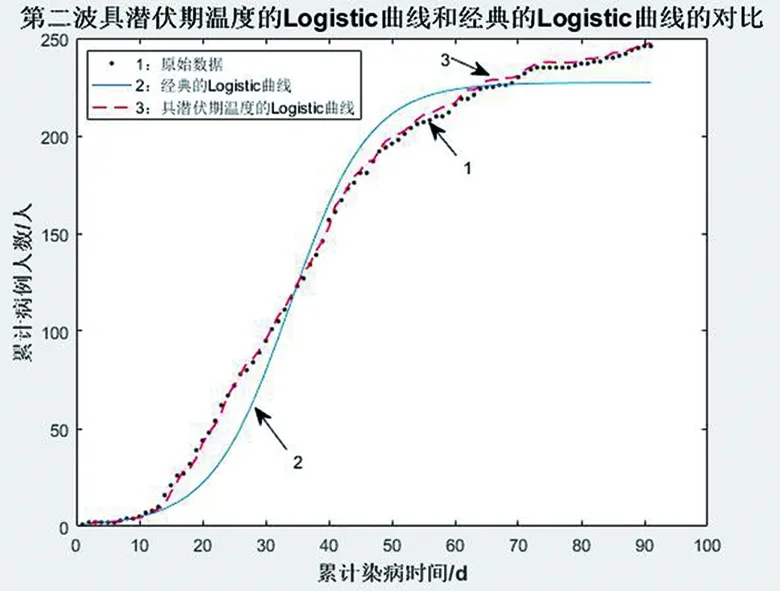
图11 第二波具潜伏期温度的Logistic曲线；原始数据；经典的Logistic曲线

(5)

其中参数θ*为病毒活性最强时的最适环境温度。将(5)式化为

N(t+1)-N(t)=[β-α(θ(t)-θ*)2]N(t)-kN2(t),

并运用数学软件Matlab的拟合工具箱，得到参数估计值为

第一波：α=0.0002127，β=0.2121，k=0.001604,θ*=15.0132,如图13所示。

第三波：α=0.002343，β=0.543，k=0.002581,θ*=6.624,如图15所示。

图13是最适温度为15.0132℃的第一波疫情的拟合曲线，图14是最适温度为8.517℃的第二波疫情的拟合曲线，图15是最适温度为6.624℃的第三波疫情拟合曲线，第一波及第二波拟合曲线与原始数据比较几乎完全接近，而第三波具最适温度的拟合曲线与原始数具有一定的偏差，误差原因可能在于第三波疫情由于数据量较少，数据之间间隔较大，故拟合曲线难以完美吻合。

但根据图13和图14可见，考虑了潜伏期温度得到的拟合曲线模拟效果很好，这说明：温度对H7N9型禽流感传播影响较大，在研究禽流感疫情控制时，温度是不可忽视的重要因素。

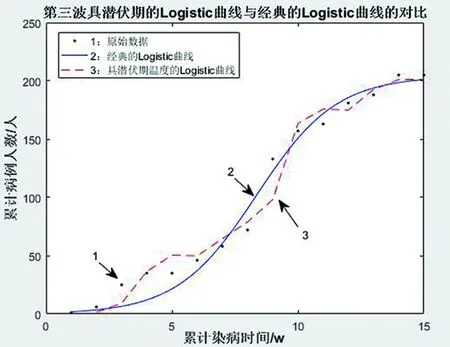
图12 第三波具潜伏期温度的Logistic曲线；原始数据；经典的Logistic曲线

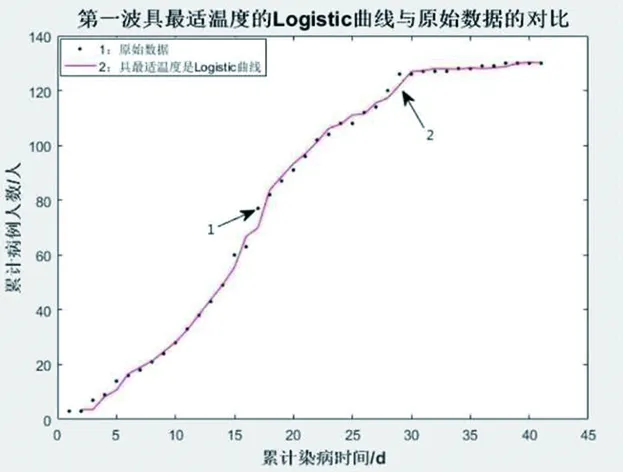
图13 最适环境温度的Logistic曲线与原始数据的对比

第二波：α=0.0000481，β=0.1012，k=0.0004199,θ*=8.517,如图14所示。

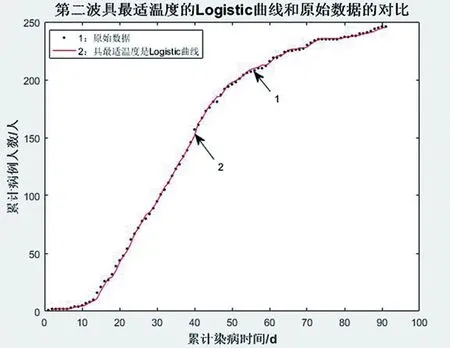
图14 最适环境温度的Logistic曲线与原始数据的对比

图15 最适环境温度的Logistic曲线与原始数据的对比

3 结 论

从上述分析和模拟的结果得出，经典Logistic模型具有一定的贴合性，但与实际病例有一定的偏差，改进后的温度模型将潜伏期温度和最适温度纳入考虑范围，进而能够较好地与实际数据相贴合，并且我们得到的三波疫情的最适温度分别为15.0132℃[10]、8.517℃、6.624℃。

从中我们可以发现，H7N9型禽流感爆发高峰期主要为冬春两季，集中在12月至次年5月期间。并且由结果表明春季禽流感的最适温度为15℃左右[11]，与实验所得数据基本吻合，而冬季禽流感的最适温度范围在6-9℃之间。此结果有助于引导大众在不同季节下做好防范措施，同时也尽量减少接触活禽的几率，避免交叉感染。另外，对于日后我国H7N9型禽流感的预防、控制工作提供了理论基础，更好地完善禽间病毒传播防控的长效体系。

此外，本文只着重考虑了温度对疫情传播的影响，未考虑政府干预[12]等其他影响因素。因此，在同时考虑这两种因素下，政府应在疫情高发季节结合所得到的最适温度对活禽加大监管力度，必要时关闭活禽市场，并且对人们进行大力宣传，科普防范措施，从而控制疫情规模。