金属线膨胀系数的研究

汪千凯

(安徽师范大学 物理与电子信息学院,芜湖 241000)

大多数物质都具有热胀冷缩的特性，物质的热胀冷缩特性直接与物质内部的原子及分子的热运动特性有关。文献[1]论述了物质的膨胀系数与物质的化学成份、物质结构、结合能、熔点、热容量、磁性以及热应力等化学及物理特性的关系，文献[2-3]从双原子模型出发，推出了金属线膨胀系数的经验公式，但对具有复杂化学结构的物质不容易给出定量的关系。

物体在一维方向上的膨胀特性用线膨胀系数来定量表述，线膨胀系数分为微分线膨胀系数以及平均线膨胀系数[1-11]，因为应用方便大多数的实际应用都采用线平均膨胀系数，所以研究线平均膨胀系数的变化规律对实际应用具有重要的意义。因为物体的长度与温度的关系一般是非线性的，所以线平均膨胀系数与物体的初始平衡温度以及温度变化的温差有关。理论上给出具有复杂化学结构的物质线膨胀系数的表达式是很困难的，对于给定材料的物体，利用实验测量的数据以及拟合方法获得线膨胀系数的经验公式是很方便并且实用的，本文利用物体的长度与温度的非线性经验关系式，在二级近似情况时，推出线平均膨胀系数与测量采样的初始平衡温度及采样温差之间的经验关系式，利用文献[11]的实验测量数据，拟合出钢45、合金铜H62以及透明石英的线平均膨胀系数的经验表达式，计算线平均膨胀系数与初始平衡温度及温差之间的关系，并且与实验结果进行比较，对结果以及理论方法的实用性将进行讨论。

1 理 论

固体的长度L与热平衡温度t的关系经验表达式为

L=L0[1+α′(t-t0)+β′(t-t0)2+γ′(t-t0)3+…)],

(1)

其中L0是物体在热平衡温度t0时的长度，α′是线性项系数，β′、γ′…是非线性项系数。若在(1)式中忽略三级及以上部分项，则

L≈L0[1+α′(t-t0)+β′(t-t0)2]。

(2)

物体的平均线膨胀系数α定义式为[3,6,11]

(3)

其中t1是物体的初始的热平衡温度，L1是物体在热平衡温度t1时的长度，t2是物体温度变化以后的热平衡温度，L2是物体在热平衡温度t2时的长度。在此必须说明的是目前关于平均线膨胀系数的定义并不一致，某些参考文献中L1不是物体在热平衡温度t1时的长度，而是在常温或者温度为20℃时的长度，但因为物体的热膨胀一般是微量的，所以L1的取值对物体的长度膨胀量的计算影响甚微。为了与文献[11]的定义式一致，本文设为热平衡温度t1时的长度。根据(2)式物体在热平衡温度t1时的长度为

L1=L0[1+α′(t1-t0)+β′(t1-t0)2]，

(4)

物体在热平衡温度t2时的长度为

L2=L0[1+α′(t2-t0)+β′(t2-t0)2]，

(5)

利用公式(3)及(4)(5)式可推得平均线膨胀系数表达式为

(6)

公式(6)中倘若

t1=t0

(7)

则

α=α′+β′(t2-t0)。

(8)

2 实验与理论结果以及讨论

文献[11]测量了材料钢45在t1=t0=0℃以及温度范围在-50～70℃时的线膨胀系数α，利用公式(8)以及文献[11]中的测量数据拟合得系数α′及β′为[12-13]

α′=11.28×10-6/℃，

(9)

β′=8.58×10-9/℃2。

(10)

则在温度范围-50～70℃内钢45的长度与温度的表达式为

L=L0(1+11.28×10-6×t+8.58×10-9×t2)，

(11)

其中L0是钢45在热平衡温度0℃时的长度。根据公式(6)以及公式(11),钢45在温度范围-50～70℃时的线平均膨胀系数近似表达式为

图1 钢45的线膨胀系数α随温差Δt的变化图线A:t1=0℃，符号°为实验结果；C:t1=-13.3℃Fig.1 The curves of linear expansion coefficient α of steel 45 with the variation of temperature difference ΔtA:t1=0℃，the sign ° represents the experimental results ；C:t1=-13.3℃

(12)

其中Δt=t2-t1。因为公式(12)中的系数α′及β′是利用钢45在温度范围-50～70℃的数据拟合获得的，所以公式(12)的适用温度范围为-50～70℃。利用(12)式可以计算出线平均膨胀系数α随温度t1及温差Δt的变化图线。图1是温度t1取定值时线平均膨胀系数α随温差Δt的变化图线，A线是t1=0℃时α随温差Δt的变化图线，符号°代表实验结果，从图中可以看出(12)式的结果与实验结果很符合，C线是t1=-13.3℃时线平均膨胀系数α随温差Δt的变化图线，从图中可以看出在t1取定值时，α与温差Δt近似呈线性关系。根据文献[11]测量的合金铜H62在t1=t0=0℃以及在温度范围-50～70℃时的线膨胀系数α的数值，利用公式(8)以及文献[11]中的数据拟合得系数α′及β′为[12-13]

α′=19.03×10-6/℃，

(13)

β′=3.28×10-9/℃2。

(14)

利用(13)、(14)、(6)可得到合金铜H62在温度范围-50～70℃内的线平均膨胀系数近似表达式为

(15)

图2 合金铜H62的线膨胀系数α随温差Δt的变化图线A:t1=0℃，符号°为实验结果；C:t1=36℃Fig.2 The curves of linear expansion coefficient α of copper alloy H62 with the variation of temperature difference ΔtA:t1=0℃，the sign ° represents the experimental results；C:t1=36℃。

利用公式(15)可以计算出线平均膨胀系数α随温度t1及温差Δt的变化图线。图2是温度t1取定值时线平均膨胀系数α随温差Δt的变化图线，A线是t1=0℃时α随温差Δt的变化图线，符号°代表实验结果。从图中可以看出式(15)的结果与实验结果很符合，C线是t1=36℃时线平均膨胀系数α随温差Δt的变化图线，从图中可以看出在t1取定值时，α与温差Δt近似呈线性关系。根据文献[11]测量的透明石英在t1=t0=0℃以及在温度范围-50～70℃时的线膨胀系数α的数值，利用公式(8)以及文献[11]中的数据拟合得系数α′及β′为[12-13]

α′=0.369×10-6/℃,

(16)

β′=2.71×10-9/℃2。

(17)

利用公式(16)、(17)及(6)可得到透明石英在温度范围-50～70℃内的线平均膨胀系数近似表达式为

(18)

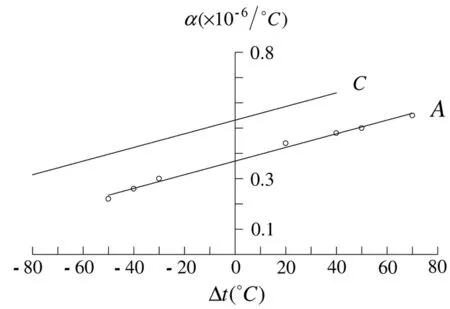
图3 透明石英的线膨胀系数α随温差Δt的变化图线A:t1=0℃，符号°为实验结果；C:t1=30℃Fig.3 The curves of linear expansion coefficient α of transparent silica with the variation of temperature difference ΔtA:t1=0℃，the sign ° represents the experimental results；C:t1=30℃

利用(18)式可以计算出线平均膨胀系数α随温度t1及温差Δt的变化图线。图3是温度t1取定值时线平均膨胀系数α随温差Δt的变化图线，A线是t1=0℃时α随温差Δt的变化图线，符号°代表实验结果。从图中可以看出(18)式的结果与实验结果很符合，C线是t1=30℃时线平均膨胀系数α随温差Δt的变化图线，从图中可以看出在t1取定值时，α与温差Δt近似呈线性关系。

从以上数据分析可以看出，线平均膨胀系数α(t1,Δt)同采样温度t1及采样温差Δt有关，公式(6)具有重要的应用价值，根据此公式可计算物体在一定温度范围内不同温度t1以及温差Δt的线平均膨胀系数，从而根据公式(3)计算物体的热膨胀长度。很显然物体的线膨胀系数与物体的热膨胀程度有关，线膨胀系数越大，表明物体在温度变化之后其长度伸缩量越大，因而计算物体在不同的t1及Δt值时的线平均膨胀系数，便可知道物体在不同的t1及Δt值时的热膨胀程度。另外根据公式(1)测量ΔL=L-L0随温差t-t0的变化数值，也可以拟合出α′、β′以及γ′等项系数，再根据公式(3)可得到物体的平均线膨胀系数的表达式。其他材料的线膨胀系数可采用类似的方法利用实验数据拟合获得。

3 结 论

物体的线平均膨胀系数与物体的初始平衡温度及温度变化的温差有关，根据物体的长度与温度的非线性关系经验公式，并利用实验测量数据很容易拟合出物体的线平均膨胀系数与物体的初始平衡温度及温差的关系公式。这种方法特别适用于具有复杂化学结构的物质以及不易得到线膨胀系数定量理论表达式的情形。