城市化、产业结构变化与经济增长的实证研究——基于全国1978—2016年统计数据

章晓英，吴 雄，李先文

（1.重庆理工大学 经济金融学院，重庆 400054；2.西南大学商贸学院，重庆 402460）

一、引言

改革开放40年来，我国经济持续高速增长，已基本实现全面建成小康社会发展的目标。但目前我国经济增长受到诸多因素影响，其中城市化水平、产业结构变化的影响非常显著，城市化、产业结构与经济增长有着密切的内在联系，城市化、产业结构变化共同作用于我国经济的增长［1］，共同影响着我国经济发展。

国内外很多学者就城市化进程对经济增长影响展开了大量研究。Black等认为空间聚集将影响人力资本积累、城市化，从而对经济增长产生影响［2］，而Duranton等认为城市的经济受到城市集中度的影响［3］。郭炳南采用我国1978—2011年的数据，通过协整检验、格兰杰因果检验和脉冲响应函数等方法，研究城市化水平、贸易自由化与经济增长之间的关系，实证结果表明城市化是经济增长的Granger原因，而经济增长对城市化发展的作用不显著［4］。吕凯波等以江苏省盐都县为例，运用合成控制法估计“县改区”对经济增长的影响，研究显示行政区划变革能加速盐都县的经济增长，但增长绩效不显著［5］。崔忠平等运用空间计量模型研究2005—2015年我国31个省份的城市化、技术溢出与经济增长之间的关系，实证结果表明技术进步和溢出、空间城市化率、人口城市化率都与经济增长存在正相关关系［6］。肖竞、任跃文等运用结构方程模型研究我国1996—2010年31个省份的城市化率对经济增长的影响，结果显示经济增长受到城市化率的推动作用显著［7-8］。方大春等基于我国31个省份2001—2012年数据，运用空间动态模型研究城市化对经济增长的影响，结果显示人口城市化对经济增长有较大的促进作用，且验证了相邻省份的城市化水平提高会对本地区经济增长有促进作用［9］。刘晓明等通过我国1986—2014年31个省份的面板数据，运用空间面板杜宾模型实证研究城市化率与经济增长的关系，结果表明城市化率与经济增长有正相关关系，并且直接效应明显低于间接效应，同时集聚效应和辐射效应将影响相邻城市的经济发展水平［10］。

关于产业结构变化对经济增长影响的研究也有很多。严成樑采用1978—2013年数据，估算了产业结构变化对经济增长的贡献，结果发现产业结构变化对中国东中西部地区经济发展的作用较大［11］。冯学良等通过空间误差模型和空间自回归模型，研究中国29个省份1993—2014年的数据，分析技术进步、产业结构变化对经济增长的影响，研究显示产业结构变化和经济增长有着显著的空间关联性，且技术进步、产业结构变化对经济增长有正相关关系［12］。陈生明等采用1997—2013年31个省份的面板数据，通过时空脉冲响应函数和半参数空间面板向量自回归模型，研究我国产业结构、技术选择与经济增长间的传导效应，结果显示产业结构变化、技术选择和经济增长在受到彼此冲击后，大多呈现正向响应特征，经济增长会促进区域产业结构升级［13］。

综述国内外研究现状发现，关于我国产业结构变化、城市化率与经济增长三者之间的实证研究成果较少。因此，本文对我国城市化率、产业结构变化和经济增长进行协整检验，分析城市化、产业结构变化对经济增长的影响，并进一步提出对策建议。

二、模型构建与检验方法介绍

（一）模型构建

1.变量选取和数据说明

本文实证研究城市化率、产业结构变化对经济增长的影响，因此模型的自变量为城市化率、产业结构变化，因变量为经济增长，所有数据均来自2017年《中国统计年鉴》。

（1）城市化率（URB）。城市化是农村人口转移到城市、农村逐渐变成城市的过程，城市化率是某个地区经济发展的重要标志［5］。参考已有研究，本文采用常住人口占总人口的比重反映城市化率。

（2）产业结构变化（ISC）。在文献梳理中，很多文章都是采用第三产业增加值与第二产业增加值作为衡量产业结构变化的动态指标［14］，而没有用三大产业增加值的占比作为产业结构变化的衡量指标，因为增加值占比仅仅表示某时间点，而不表示一个动态过程。故用第三产业增加值与第二产业增加值之比来代表产业结构变化指标：

其中：ISC表示产业结构变化，X3表示第三产业增加值，X2表示第二产业增加值。

（3）经济增长（GDP）。国内外学者采用GDP增长率、GDP总量等作为衡量经济增长的指标。但是中国是一个人口大国，如果以GDP总量或GDP增长率来衡量经济增长，可能不够准确，因此本文采用人均GDP作为经济增长的评价指标，同时以1978年为基期对GDP数据剔除了物价波动的影响。

2.建立模型

本文基于VAR模型进行协整检验、Granger因果检验和脉冲响应分析。VAR模型不以严格的经济理论为依据，只需明确哪些变量是相互有关系的以及滞后阶数，模型的预测较为准确、方便。因此把模型设定为：

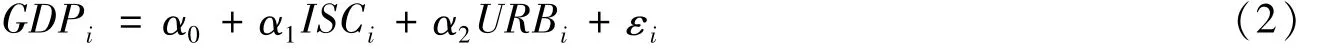
其中：i代表年份，GDP表示经济增长，ISC表示产业结构变化，URB表示城市化率。同时，为了减小异方差的影响，对3个变量都进行取自然对数处理，得到模型如下：

（二）检验方法介绍

1.平稳性检验

许多时间序列都是不平稳的，常有“伪回归”的现象出现，所以时间序列需要做平稳性检验，需要对出现不平稳的变量进行对数化或者多重差分处理。序列平稳性常用单位根检验方法，本文用ADF检验来验证平稳性，模型如下：

式（4）表示没有常数，没有时间项；式（5）表示有常数，无时间项；式（6）表示既有时间项，又有常数项。

2.协整检验

1987年Granger和Engle提出的协整理论和方法成为分析非平稳经济变量间关系的最主要工具。当这些经济变量线性组合时，有可能让它们变成平稳序列，而这种平稳性的线性组合叫协整方程。协整检验分为两种：一种是基于回归残差的协整检验，即JJ检验，另一种是基于回归系数的协整检验，即E-G两步法，本文采用JJ检验。

3.格兰杰因果关系检验

格兰杰因果关系检验是用来研究一个变量的当前行为是否会受到过去行为的影响，两个有相关关系的变量之间是否具有因果关系，是单向因果还是双向因果。检验模型如下：

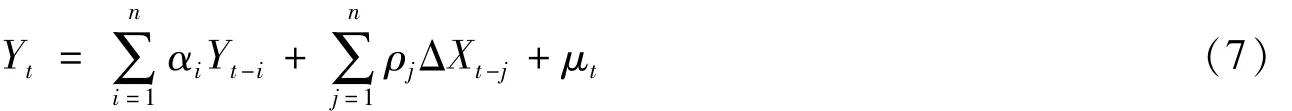
4.脉冲响应

脉冲响应用来测定不同时期内生变量对所有变量的冲击效果，同时反映变量间的相关效应。而这样的反映效果，实质是内生变化对其他变量的作用，同时影响内生变量本身的过程。

三、实证分析

（一）平稳性检验

对Ln GDP、Ln ISC、Ln URB 3个变量进行平稳性检验（表1），结果显示，Ln GDP、Ln ISC、Ln URB对应的时间序列数据在没有任何处理前具有不平稳性，但通过一阶差分后都有了平稳性。

（二）协整检验

1.确定协整滞后阶数L

在进行向量自回归（VAR）模型估计时，最主要是确定滞后阶数取值，滞后阶数越大越能够反映模型的动态特点，而滞后阶数增加会使自由度减少，因此选择合适的滞后阶数非常重要。本文运用FPE、SC、LR、AIC、HQ 5个指标来确定最佳滞后阶数为2，结果如表2所示。

表1 各变量平稳性检验结果

表2 最佳滞后期检验结果

2.协整向量个数r的检验

Granger和Engle提出的“协整理论”解决了非平稳序列建模问题，他们认为，如果两个非平稳序列变量是同阶单整，同时两个非平稳序列变量的线性组合是零阶单整，则这两个变量间存在长期均衡关系。前面的平稳性检验已经看出3个变量Ln GDP、Ln ISC、Ln URB是一阶单整的，存在长期均衡关系，现在需要确定协整向量个数r。

由表3中特征值、迹统计量可以看出，迹统计量在5%的显著水平下拒绝没有协整关系的假设，表明ln GDP、ln ISC、ln URB之间存在协整关系。

表3 多变量Johansen协整检验结果

3.协整方程

经济增长、产业结构变化和城市化率3个变量的协整方程为（括号内的数字是t统计量值）：

从式（8）可知，长期来看，城市化率、产业结构变化对经济增长的影响都呈正相关关系，且城市化率

对经济增长的影响大于产业结构变化对经济增长的影响。

（三）误差修正模型和检验

协整分析与Johansen检验的结果一致，选取L＝2。表4显示的是VECM的参数估计结果（括号内的数字是t统计量值）。

从误差修正模型看出，在做格兰杰因果检验和脉冲响应函数前，需进行检验。从图1和表5的稳定性检验可知，在单位圆上有两个根，其他值都在圆内，所以满足误差修正模型的稳定性条件。从LM（拉格朗日乘数检验）自相关检验看出，当LM1为9．787时，P值为0.368，而当 LM2为9．124时，P值为0．426，因此不存在自相关。从White异方差检验看出，当 χ2值为 90．664时，P值为0.290，即不存在异方差。联合正态性检验结果可以看出，当J-B值为3．354时，P值为0．763，符合正态分布。

所以，误差修正模型较为稳定，从误差修正得出Granger因果关系和脉冲响应是可靠的。从表4可知，D（ln GDP）误差修正项系数为-0.005，符合误差修正的调整方向。

图1 VAR（2）的单位圆检验

表4 误差修正模型估计结果

表5 误差修正的稳定性检验结果

（四）格兰杰因果检验

协整检验表明3个变量之间有长期均衡关系，但不能判断它们之间是否有因果关系，而分析中往往需要知道它们间的因果关系，方便做下一步的实证分析。为此，在上述协整检验基础上，对经济增长、城市化率和产业结构变化进行格兰杰因果检验，判断这3个变量之间的因果关系，结果如表6所示。

表6 Granger因果检验结果

由表6可以看出产业结构变化、城市化率对经济增长的检验拒绝原假设，同时经济增长对产业结构变化和城市化率的检验也拒绝原假设，表明产业结构变化、城市化率与经济增长之间有双向Granger因果关系。城市化率对产业结构变化的检验拒绝原假设，表明城市化率是产业结构变化的单向Granger原因，即城市化率的提高将影响到产业结构调整并带来资本、设备、技术的不断升级。

（四）脉冲响应分析

图2是基于VECM模型的脉冲响应函数，纵轴表示经济增长受产业结构变化、城市化率冲击的响应程度，横轴表示滞后期数。脉冲响应图用来分析随机扰动项冲击对变量的影响。

根据脉冲响应函数图，经济增长受到城市化率的正向冲击后，表现为正，且城市化率的增加将促进经济增长的增加，在滞后第2期时到达冲击效应的最高值，而后下滑直至平稳，因此从长期来说，城市化率的增加对经济增长有较强的促进作用。同时，产业结构变化对经济增长冲击后，长期为正的冲击效应，但短期为负的冲击效应。在滞后期1～3年，经济增长受到一个单位正向标准差产业结构变化的冲击，且冲击效应为负，但三期后冲击效应逐渐从负效应变成正效应，直至平稳。

综合来看，这里的结论与前面的协整检验结果是一致的，产业结构变化和城市化率都对经济增长有显著的促进作用。这里产业结构变化的短暂负影响也是符合实际的，主要原因是，随着中国经济的发展，产业结构的转型升级带来了技术创新、机械设备的更新换代等，而这些产业结构的转型升级无法在短时间内完成，所以将会在短期内对经济增长产生负效应的影响，而产业结构转型升级的完成，将会对经济增长有显著的促进作用。

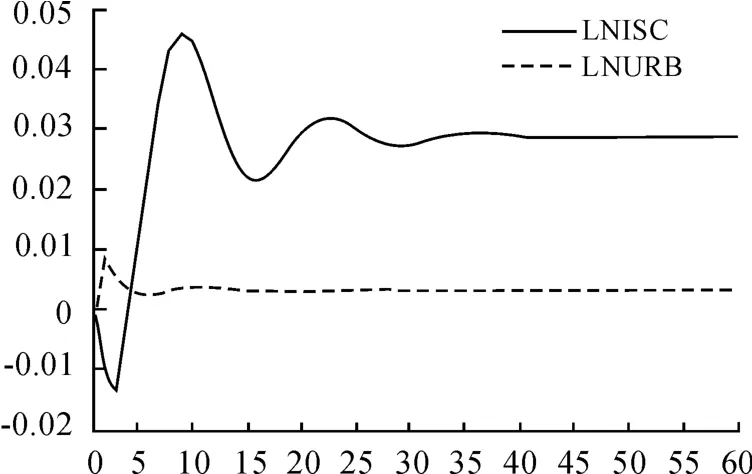
图2 ln GDP受到ln ISC、ln URB冲击的脉冲响应曲线

四、结论与对策建议

（一）结论

本文运用1978—2016年的年度时间序列数据，选取产业结构变化、经济增长和城市化率作为研究对象，构建产业结构变化、城市化率对经济增长的长期均衡方程。运用ADF、协整检验、Granger检验和脉冲响应函数，研究三者之间的关系。从上述实证分析得出，产业结构变化、城市化率能够促进经济增长，同时经济增长也能促进城市化率和产业结构变化。

协整检验结果表明，产业结构变化与城市化率都在不同程度上促进了经济增长，但两者作用有差异，产业结构变化影响小于城市化水平，说明在我国经济增长中，产业结构转型升级较慢，产业结构对资本、技术、人员的要求较高。因果关系检验表明，城市化率和产业结构变化与经济增长都呈现双向因果关系，城市化率和产业结构变化共同促进经济增长，同时经济增长也能够促进城市化率和产业结构变化，而城市化率是产业结构变化的单向Granger原因，城市化率能够促进产业结构变化。从脉冲响应函数图来看，城市化率对经济增长长期是正向积极作用，所以在提高城市化水平的同时，也要考虑过度城市化带来的负面影响。而产业结构变化短期会导致经济增长负效应，但长期来看，产业结构调整对经济增长有积极作用，开始增长速度较快，后面增长速度较平缓。其原因可能是产业结构在调整时，会对经济增长有抑制作用，但产业结构调整完成后，能够大幅度促进经济增长。因此，处理好经济增长、产业结构变化和城市化率之间的关系，更能够实现经济的长期稳定发展。

（二）建议

产业结构变化、城市化与经济增长三者间是相互影响的，在未来发展中一定要重视三者之间的关系。目前，我国经济处于转型期，产业结构调整较慢，城市化水平的质量和层次较低，城市化对经济增长的促进作用还不强，对此提出以下建议：

（1）需要加快城市化进程的速度。中国是一个农业大国，从户口上来看，我国依然有大部分的人是农村户口，为减少农村人口的比例，除了降低农业对人口的依赖，让农村人口转移到城市外，还可以通过大力发展第三产业吸引农村人口进入城市，大量人口涌进城市带来了城市化发展、技术进步，从而带动经济增长。但由于户籍制度的影响导致那些从农村进入城市的人口无法真正留在城市，影响城市化的进程。对此，需要加强户籍改革，以及土地、房地产等领域的改革，加强科技成果的转化率，进一步提升城市化率对经济增长的促进作用。

（2）加快发展第三产业，不断优化产业结构。要想解决第二产业对就业带来的不利影响，就需要大力发展第三产业，当前我国第三产业对就业的拉动已超过40%，且这比重还在不断增加。从发达国家经验看，我国的第三产业发展潜力很大，对城市化率和就业率的影响较大。同时因为第三产业主要以服务性产业为主，具有低资源消耗、绿色环保的特点，发展第三产业不仅对社会和经济发展有促进作用，而且对城市化率有较强的推动作用。产业结构调整是经济发展的主动力，需要逐步完善区域经济空间布局，整合自然资源，提高资源利用率，形成新的增长极和发展机遇。

（3）无论是城市化率的提高还是产业结构的转型升级，最后都是为社会发展服务，在过去我国特别强调城市化率的大小，而忽略了过度城市化带来的不良影响。所以不能因为追求城市化率而不考虑社会和谐发展的重要性，需要把握好经济发展的客观规律，正确看待结构与速度之间的关系，只有这样才能促进我国经济更加快速、平稳、持续的发展。