基于遗传算法的钣金件下料问题优化研究

孟子暄

（河北工业大学经济管理学院， 天津 300400）

引言

板材下料问题又称为二维板材排样问题（Nesting Problems），是指将一系列二维平面图形互不交叉的放置在某一板材上，使得所覆盖的板材面积最大[1]。对于企业而言，板材的利用率越高，越节约材料，所用成本越少，对提高企业经济效益起到关键作用。

将遗传算法与改进后的BL算法进行结合，解决矩形件排样问题，取得了不错的排样效果。但本文运用遗传算法与最低水平线法相结合，解决了BL算法的局限性。

1 排样问题及数学描述

假设板材的长度为L，宽为W，面积为S，需要切割的小板材长为xi，宽为yi（i表示第i种需要切割的小板材，i=1，2，3…，n），板材剩余面积为 Areal。当零件横放时占用的空间为li，竖放占用的空间是ki。xili表示在原料板上第j块区域内横放零件的行数；yiki表示板材上第j块区域内小板材竖放的行数。nj表示板材上第j块区域内零件横放时每行的个数；mj表示大板材上第j块区域内小板材竖放时每行的个数。

本研究目标：板材利用率最高，即板材剩余面积最小。

排放基本原则：将所需零件排放在定长定宽的原材料板中，零件的长或宽与原材料板平行，零件之间不可交叉，且不得超过原材料板的长或宽。即满足：

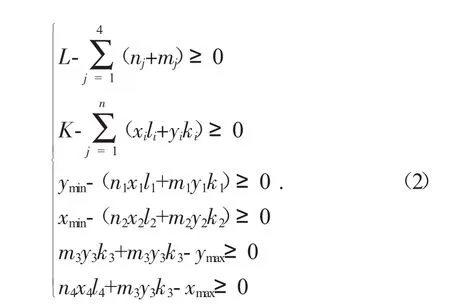
根据给出的约束条件和目标函数的数学模型，评估各个染色体的优劣，筛选出符合该数学模型的可行解，该可行解即为最优解。

2 遗传算法

2.1 染色体编码与解码

染色体编码是遗传算法最关键的步骤，其是一种可以将实际待优化问题的可行解转化到遗传算法可以处理的搜索空间中的一种方法。本文采用整数编码，对待排零件按顺序进行编码，例如 2、3、5、1、4 代表将零件如图1所示顺序进行依次排放，0代表零件横放，1代表零件竖放。运用“最低水平线”进行解码。

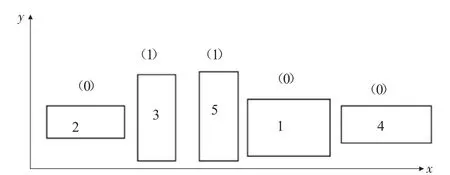
图1 板材排放顺序示意图

2.2 种群初始化

随机产生N个染色体作为初始种群，遗传过程中的收敛速度会受到初始种群大小的影响，因此N的取值应选择适当，一般N取值在50～200之间，本文N选取60。

2.3 适应度函数

适应度函数指引着遗传算法的搜索方向，适应度函数的选择应该根据具体的问题而定，本研究中适应度函数为板材剩料率，即为目标函数。

2.4 遗传算子

2.4.1 选择算子

轮盘赌选择算法是遗传算法中最常用的选择算法，其根据群体中每个染色体的适应值得到群体所有染色体的适应值总和，并分别计算每个染色体适应值与群体适应值总和的比pi；较优染色体的pi值较大，被选择的概率就相对较大。

2.4.2 交叉算子

交叉操作是遗传算法中的的核心操作步骤,是种群中产生新个体的主要途径之一。一般情况下,设置交叉概率为0.4～0.9之间。

本文涉及的交叉操作算子方法为：首先在染色体上选择一个位置作为交叉位置，交叉位置之前的基因片段不交叉，交叉位置之后的片段交叉。

去除染色体X和Y的不变片段中相同基因，将X染色体中剩余基因存至数组P中，同理，将Y染色体中剩余基因存至数组Q中。

将染色体X和Y的交叉部分进行比较,将相同部分进行替换，替换之后染色体符合实际要求。

2.4.3 变异算子

在遗传算法中，产生新一代的个体主要依靠的是选择和交叉，变异操作是一种产生多样性个体的辅助手段，变异算子设计的好坏能决定算法的局部搜索能力。变异概率较小，一般设为0.000 1～0.1之间。

3 实例验证

为了检验遗传算法在求解工程二维不规则排样问题方面的有效性，本文以K公司为例，从其套料零件数据库中随机选取了一组具有不同形状的多种类、多数量零件进行混合排样计算，零件种类为10种，零件总数量为44，加工余量为2 mm，从板材库中选择矩形板材长为2 500 mm，宽为1 250 mm；设置算法基本运行参数:种群大小200、初始交叉率0.16、变异率0.106，设置最大迭代数为500，调用遗传算法确定零件的排放顺序和旋转角度，用基于最低水平线法策略的动态扫描线算法的解码定位算法确定零件在板材的位置。排样布局如图2所示。

图2 多种矩形件算法排样结果示意图

优化结果与公司实际排样结果对比如表1所示。

表1 算法结果对比示意表

根据上述结果对比可以看出，本文算法具有很好的稳定性，寻优运行时间较短，板材利用率更高，具有很强的工程实用价值，因此，本文遗传算法能够有效求解矩形零件的排样问题。

4 结语

针对钣金矩形件的排样问题，本文提出运用遗传算法进行优化，将板材运用整数顺序编码法进行编码，运用最低水平线算法进行解码的方法对矩形件运用遗传算法进行优化求解，运算结果显示，该算法优于公司实际排样效果，大大提高板材利用率，节约公司成本。