细品真题 多解拓展——2018年全国卷Ⅰ理第19题

江苏 韩文美

著名数学家、教育学家G·波利亚在《怎样解题》一书中指出：“好题目和某种蘑菇有点相似之处：它们都是成串成长，找到一个以后，我们应该看看，很有可能在很近的地方又能找到更多的．”2018年高考过后，数学风云，创新无限，名题如云，美不胜收．特别是2018年高考全国卷Ⅰ理第19题，背景简单，立意新颖，思想丰富，知识融合，动静结合，实属难得，是名题中的一大精品，具有非常好的学习、观摩、研究、拓展的价值．

一、真题在线

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB．

分析：本题涉及椭圆的方程与几何性质，直线与椭圆的位置关系，直线的方程与斜率，考查函数与方程思想，数形结合思想，化归与转化思想等．解题的关键是证明∠OMA=∠OMB时所切入的角度，可以利用直线的斜率和为零，也可以利用角平分线的性质，还可以利用几何法、参数方程法等方法．不同的切入点有不同的解法，多点思维，多向开花．

二、多向思维

当我们解完一道题以后，要不断领悟反思，多角度切入进行深度挖掘，从而达到触类旁通、一题多解的效果．

【解析】方法1：(标准答案)

(1)由已知得F(1，0)，则直线l的方程为x=1，

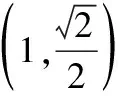
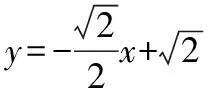
(2)当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB；

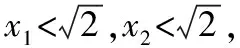
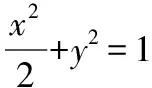
从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB；

综上，∠OMA=∠OMB．

方法2：(标准答案的改进)

(1)同方法1；

(2)当l与x轴重合时，∠OMA=∠OMB=0°；

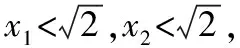
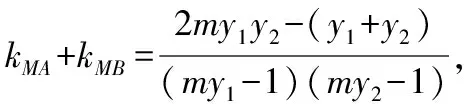
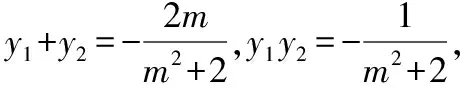
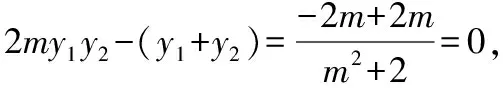
从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB；

综上，∠OMA=∠OMB．

方法3：(角平分线的性质法)

(1)同方法1；

(2)当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1(m∈R)，A(x1，y1)，B(x2，y2)，

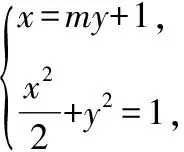
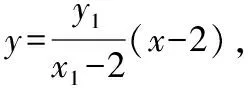
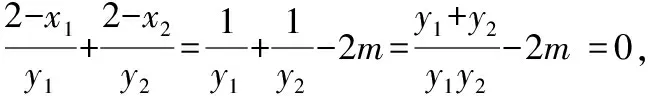
所以x轴为∠AMB的平分线，则有∠OMA=∠OMB，

综上，∠OMA=∠OMB．

方法4：(几何法)

(1)同方法1；

(2)当l与x轴重合时，∠OMA=∠OMB=0°；

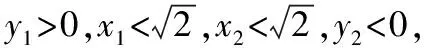
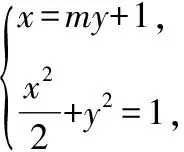
分别过点A，B作x轴的垂线，垂足分别为D，E，

综上，∠OMA=∠OMB．

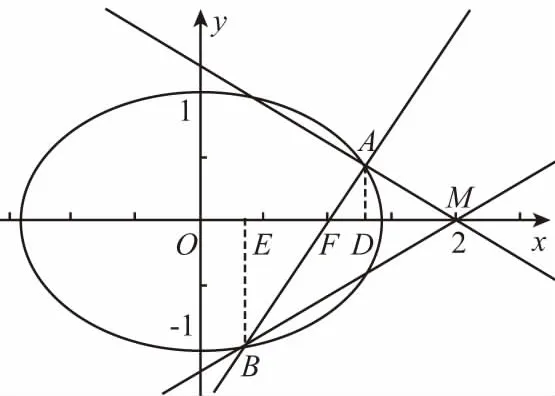
方法5：(对称性法)

(1)同方法1；

(2)当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1(m∈R)，A(x1，y1)，B(x2，y2)，

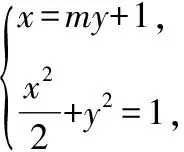
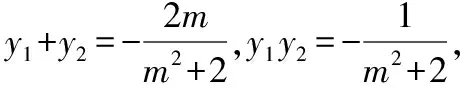
根据椭圆的对称性，∠OMA=∠OMB等价于点B关于x轴的对称点B′(x2，-y2)在直线AM上，

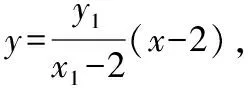
所以∠OMA=∠OMB．

方法6：(向量法)

(1)同方法1；

(2)当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1(m∈R)，A(x1，y1)，B(x2，y2)，

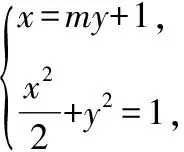
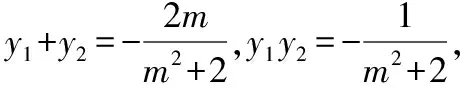
由于∠OMA=∠OMBcos∠OMA=cos∠OMB2my1y2-(y1+y2)=0，

所以∠OMA=∠OMB．

方法7：(参数方程法)

(1)同方法1；

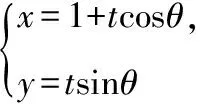
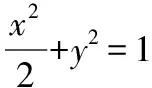
直线MA，MB的斜率之和为

从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB．

三、变式拓展

通过该题深入分析，改变条件，拓展思维，可以得到意想不到的效果，真正达到“认真解答一个题，拓广解决一类题，变式深化一片题，思维能力一起升”的美好目的．

变式方向1：改变证明结论，目标更为明确，难度相当

(1)当l与x轴垂直时，求直线AM的方程；

(2)试确定直线MA，MB的斜率之和为kMA+kMB是否为定值？若是，请求出该定值；若不是，请说明理由．

解析：(1)由已知得F(1，0)，l的方程为x=1，

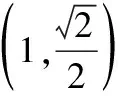
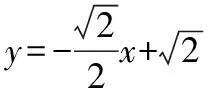
(2)直线MA，MB的斜率之和为kMA+kMB=0，为定值．

当l与x轴重合时，kMA+kMB=0；

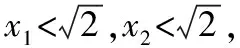
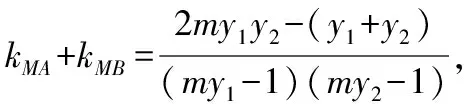
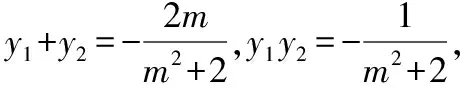
故直线MA，MB的斜率之和为kMA+kMB=0，为定值．

点评总结：根据高考真题以及变式1，可得一般性的结论：

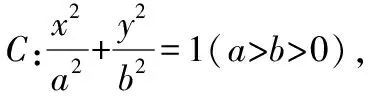
变式方向2：改变圆锥曲线类型及其相关条件，难度相当

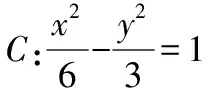
(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB．

解析：(1)由已知得F(3，0)，l的方程为x=3，

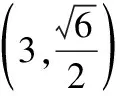
(2)当l与x轴重合时，∠OMA=∠OMB=0°；

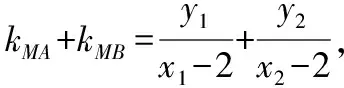
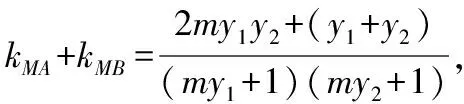
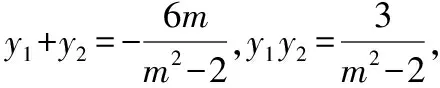
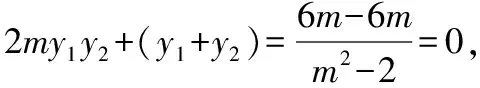
从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB；

综上，∠OMA=∠OMB．

点评总结：根据变式2，可得一般性的结论：

变式方向3：改变圆锥曲线类型及其相关条件，难度相当

【变式3】(2018·全国卷Ⅰ文·20)设抛物线C：y2=2x，点A(2，0)，B(-2，0)，过点A的直线l与C交于M，N两点．

(1)当l与x轴垂直时，求直线BM的方程；

(2)证明：∠ABM=∠ABN．

解析：(1)当l与x轴垂直时，直线l的方程为x=2，可得M的坐标为(2，2)或(2，-2)，

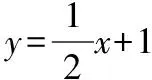
将x1=my1+2，x2=my2+2及y1+y2，y1y2的表达式代入①式分子，可得x2y1+x1y2+2(y1+y2)=2my1y2+4(y1+y2)=-8m+8m=0，

所以kBM+kBN=0，可知BM，BN的倾斜角互补，所以∠ABM=∠ABN．

点评总结：根据变式3，可得一般性的结论：

【定理3】已知点M(m，0)，N(-m，0)(m≠0)与抛物线C：y2=2px(p>0)，过点M作与x轴不平行的直线l交抛物线C于A，B两点，则直线AN，BM与x轴成等角．