关于复指数函数的定义
2018-12-06 02:59:54段江梅
昭通学院学报 2018年5期
段江梅
(昭通学院 数学与统计学院,云南 昭通 657000)
1 引言
在复变函数中,复指数函数ez是最主要也是最简单的初等函数.因此复指数函数的定义及其性质是初等函数中的重点研究对象.在经典教材钟玉泉编《复变函数论》及B.B.沙巴特编《复分析导论》中给出指数函数的定义.
定义1 对于任何复数z=x+iy,用关系式
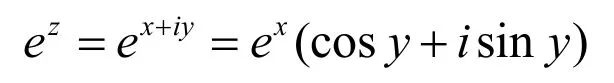
来规定指数函数ez.
定义2 用极限关系来定义指数函数ez

下面给出这两种定义的构造形式.
2 复指数函数的定义
2.1 定义1的构造形式
(1)当y=0 时,f(z)=ex,这个函数就是实指数函数.
(2)f(z)在z平面上解析,且

这四个偏导数在z平面上处处连续,且满足方程,因此在z平面上解析,并且实指数函数具有类似的性质.
(3)进一步,还易验证:

实指数函数同样具有类似的性质.
事实上,由条件(1)(3)知

又因f(z)在z平面上解析,故由C.-R.方程得
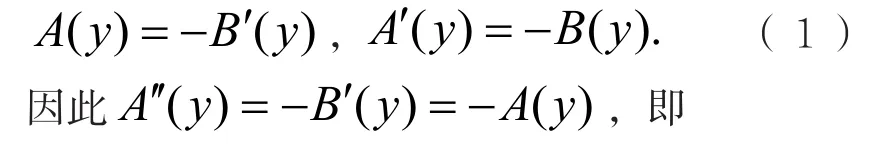

这是二阶常系数齐次线性微分方程,方程的通解为

其中c1,c2为任意常数.
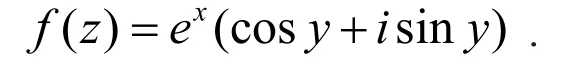
2.2 定义2的构造形式
像在实分析中一样以极限关系来定义指数函数ez:

下面证明这个极限对于任意z∈C的存在性.
为此令z=x+iy,并注意到,由幂的提升规律有
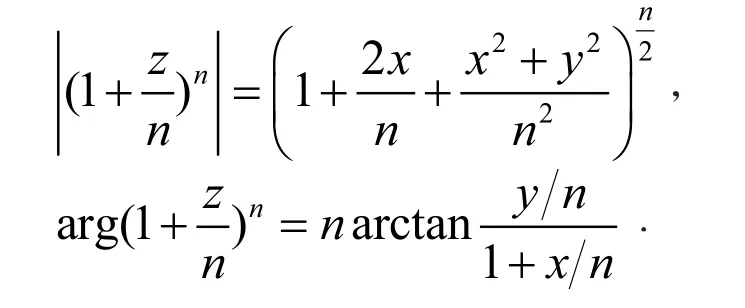
由此看出,存在

这意味着极限(4)存在,并且可以写为极坐标形式:
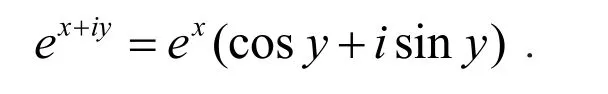
猜你喜欢
昭通学院学报(2022年1期)2022-05-28 07:36:32
新世纪智能(数学备考)(2021年9期)2021-11-24 01:14:36
新世纪智能(数学备考)(2021年9期)2021-11-24 01:14:34
中学生数理化(高中版.高二数学)(2021年5期)2021-07-21 02:14:46
新世纪智能(数学备考)(2020年9期)2021-01-04 00:25:12
新世纪智能(数学备考)(2020年9期)2021-01-04 00:25:12
中等数学(2020年6期)2020-09-21 09:32:38
中等数学(2019年6期)2019-08-30 03:41:46
中学生数理化·七年级数学人教版(2018年4期)2018-06-28 03:26:30
西南学林(2014年0期)2014-11-12 13:09:16

