例析数学思维在解答地理计算题中的妙用

河南 李跃进

众所周知，地理是一门综合学科，兼有自然科学和人文科学的思维方法。数学是自然科学的基础，它的思维方法又渗透在中学的各个学科中，因此，用数学思维解答地理计算题，可以收到事半功倍的效果。笔者一些典型题目进行了认真研究，受益匪浅。现本文以几道题目为例简要介绍几种数学思维在解答地理解计算题中的妙用，以当引玉之砖，供读者参考。

一、数学公式求解法

数学公式是人们在研究自然界时所发现的不同事物之间数量关系的一种表达方法，它确切地反映了事物内部和外部的联系。由于数学公式是根据一定的规则或标准、由公理和定理严密地演绎推理得出来的结论，因此它的科学性是不容怀疑的。对于自然地理中规律性强的地理计算题，运用数学公式求解法往往十分有效。例如，正午太阳高度、昼夜长短、晨昏线、时间与日期、陡崖高度、球面距离等计算公式，平时要多注意积累与自然地理相关的数学公式，并且正确使用与数学相关的计算公式。

【例1】(2015年浙江卷·11)下图为某地地方时12时的太阳周年位置轨迹示意图。

若甲、乙两个位置的太阳高度之和为90°，则乙位置太阳高度为

( )

A．47° B．43° C．23.5° D．21.5°

【解析】本题考查正午太阳高度的季节变化规律，主要利用某地一年内的正午太阳高度最大差值计算公式。假设某地一年内的最大正午太阳高度为Hmax、最小正午太阳高度为Hmin，则该地一年内的正午太阳高度最大差值为Hmax-Hmin。可以分为两种情况：若该地位于南北回归线以外，则Hmax-Hmin=黄赤交角×2=47°；若该地位于南北回归线之间，则Hmax-Hmin=黄赤交角+当地纬度。由图可知，甲、乙两个位置的太阳高度分别是该地一年内的最大正午太阳高度为Hmax和最小正午太阳高度为Hmin，因此Hmax+Hmin=90°；由题意可知，该地一年内无阳光直射现象，应位于南北回归线以外，因此Hmax-Hmin=47°；由Hmax+Hmin=90°、Hmax-Hmin=47°可求得Hmax=68.5°、Hmin=21.5°。故选D项。

二、算术表达求解法

算术表达式是指数学课程中由数字和运算符号组成的式子，可以简单清晰地记录或描述计算过程和内容。地理计算题的已知条件往往会涉及一些相关的地理概念，这些概念有的是教材中已经学过的，如气温垂直递减率、人口自然增长率、城市人口比重等；有的则是材料给出的情境概念，如人口红利、城市首位度、产业结构偏离度、劳动力利用效率等。在解答与地理概念相关的计算题时，将地理概念转化为算术表达式，可以有效理清解题思路，从而化繁为简。

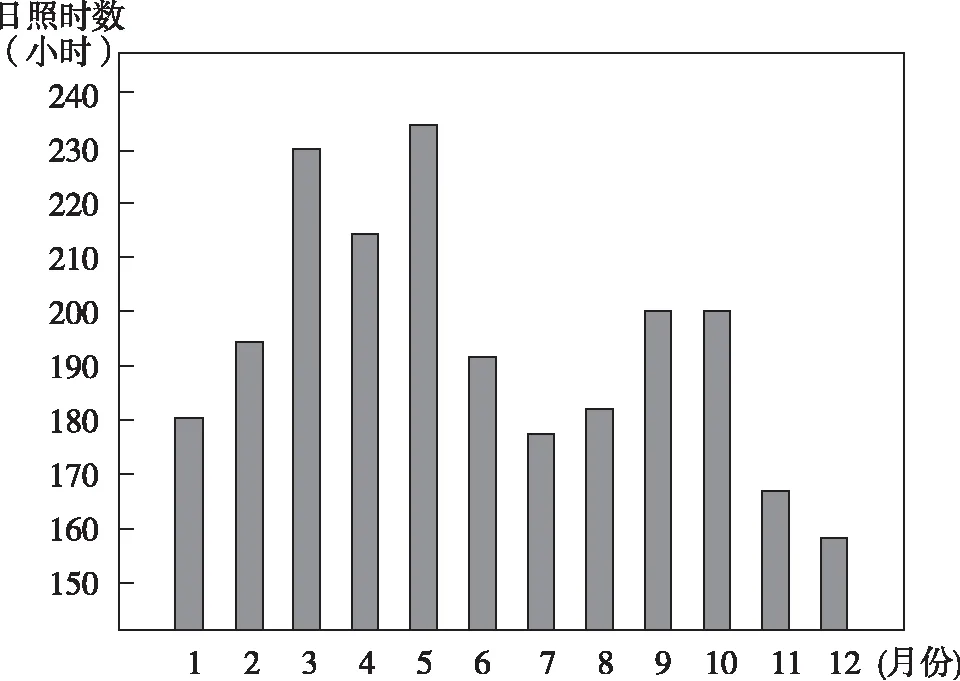
【例2】(2015年山东卷·8)日照时数指太阳在某地实际照射的时间。图们江是中国与朝鲜的界河。下图为图们江流域日照时数年内变化柱状图。日照百分率为一个时段内某地日照时数与理论上最大的日照时数的比值(﹪)。

该流域3月份的日照百分率约为

( )

A．53% B．62% C．70% D．78%

【解析】本题考查区域日照百分率计算和读图分析能力。题目中核心概念的数学表达式为：日照百分率=实际日照时数/理论日照时数。由图可知，图们江流域3月份的实际日照时数约为230小时，解答该题的关键是求出图们江流域3月份的理论日照时数。理论日照时数就是白昼时间长短，3月份在春分日(3月21日)附近，全球各地大致昼夜平分，每天的理论日照时数约为12小时，整个3月份的理论日照时数约为12小时×31=372小时。因此，该流域3月份的日照百分率=(230小时/372)×100%小时=62%。故选B项。

三、集合理论求解法

集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体，这些对象称为该集合的元素；交集是指由若干个集合的相同元素组成的集合，这些相同元素称为该交集的元素。对于同时满足多个条件的地理计算题，运用集合理论求解法往往十分有效。例如，某道地理计算题让求“此时赤道上和北京在同一日期的东半球的白昼范围”，就可以把赤道上东半球的范围、白昼的范围和北京在同一日期的范围看作三个集合，那么本题所求的范围就是这三个集合的交集。

【例3】(2015年全国新课标卷Ⅱ·8)1996年我国与M国签订海洋渔业发展合作规划，至2010年我国有20多家沿海渔业企业(总部设在国内)在M国从事渔业捕捞和渔业产品加工，产品除满足M国需求外，还远销其他国家，下图示意M国的位置。

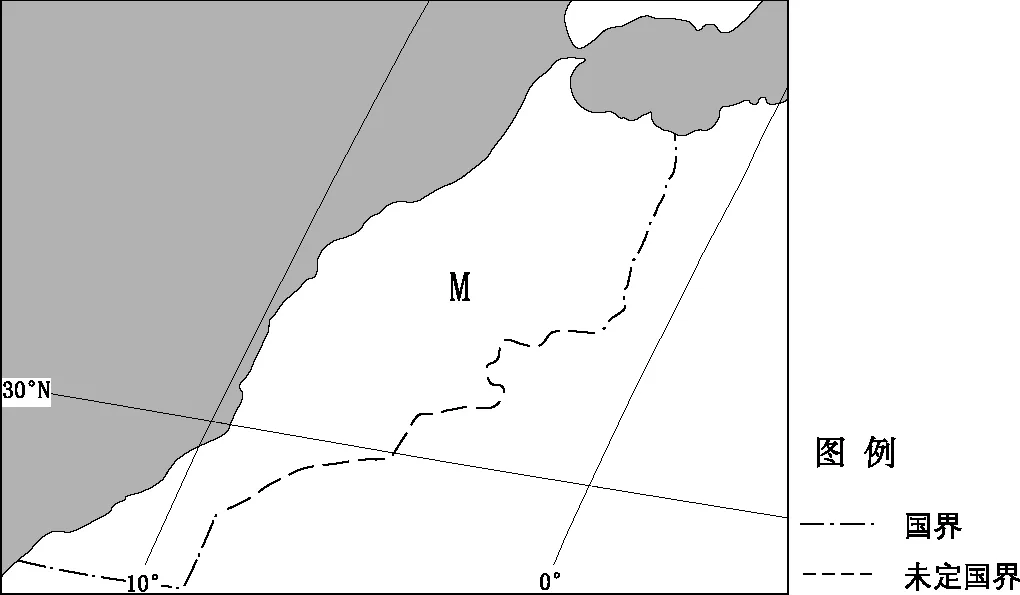
如果都以当地时间8：00—12：00和14：00—18：00作为工作时间，在M国的中资企业若在双方工作时间内向其总部汇报业务，应选在当地时间的

( )

A．8：00—9：00 B．11：00—12：00

C．14：00—15：00 D．17：00—18：00

【解析】本题考查地球运动的地理意义(区时计算)。由题意可知，所选的时间范围应该是企业总部工作时间和中资企业工作时间两个集合的交集。由图可知，位于M国的中资企业使用的时间是0时区区时，而位于我国的企业总部使用的时间是东8区区时，因此中资企业使用的时间比企业总部使用的时间晚8个小时。当位于我国的企业总部处于工作时间(8：00—12：00和14：00—18：00)时，位于M国的中资企业的当地时间应该是0：00—4：00和6：00—10：00。故选A项。

四、比例关系求解法

比例是指数学上表示两个或多个比相等的式子，其基本性质是两个外项积等于两个内项积，运用该性质可以求得比例中的未知项。对于两个比能组成比例的地理计算题，运用比例关系求解法往往十分有效。例如，某道地理计算题让求“在图上距离3.6厘米表示实际距离1 080千米的地图上，4.8厘米表示的实际距离是多少千米”，就可以根据比例尺的概念先确定图上距离与实际距离的比均相等，然后再列出比例关系3.6∶1 080=4.8∶X，从而求出4.8厘米表示实际距离X=1 440千米。

【例4】(2015年重庆卷·12)马尔代夫是以旅游业为支柱产业的著名岛屿。2014年12月4日，马累海水淡化厂设备摧毁导致该岛淡水供应中断。应马尔代夫政府请求，中国政府及时向其提供了饮用水等物资和资金援助。下图是马尔代夫部分区域示意图。

中国一架满载饮用水的飞机紧急从广州飞往马累，若北京时间12：00出发，经4小时到达马累。机长身高为1.8m，到达时其在机场地面的身高影长接近于(tan55°≈1.43，tan65°≈2.14)

( )

A．0.6 m B．1.2 m C．1.8 m D．2.4 m

【解析】本题考查正午太阳高度角的计算和应用。解答本题需要以下四个步骤：(1)计算飞机到达马累机场时的当地地方时(13：00)，(2)计算该日马累的正午太阳高度(66°)，(3)计算飞机到达马累机场时的太阳高度(55°)，(4)计算机长在机场地面的身高影长(1.2m)。其中，第三步运用到了比例关系求解法。具体解法为：①确定马累该日的太阳高度变化范围。由地球运动规律可知，马累位于赤道附近，一天内太阳高度的变化范围约为正午太阳高度的4倍。②确定具有比例关系的两个比。马累的太阳高度变化之比与时间变化之比具有比例关系，设马累该日的正午太阳高度为H，在T小时内马累太阳高度的变化为X，则有X：4H=T：24。③确定马累1小时内的太阳高度变化范围。在X：4H=T：24中，H=66°，T=1小时，可求得X=11°。④确定飞机到达马累机场时的太阳高度。马累该日的正午太阳高度为H=66°，飞机到达马累机场时的当地地方时为13：00，此时马累机场的太阳高度约为66°-11°=55°。由tan55°≈1.43，机长身高1.8m可计算出影长约为1.2m，故选B项。

五、区间限定求解法

区间是指数学上能表示在数轴上的不等式解集的一种表示方法，根据是否包含端点可以分为闭区间、开区间、左闭右开区间、左开右闭区间。对于含最大值和最小值的地理计算题，运用区间限定求解法往往十分有效。例如，某道地理计算题让求“等高距为50米的等高线地形图中，有4条等高线重叠的陡崖的可能相对高度”，就可以先求出陡崖相对高度的最大值(250米)和最小值(150米)，然后确定陡崖相对高度的限定范围[150，250)，从而求出可能的相对高度。

【例5】(2015年全国新课标卷Ⅰ·6)甘德国际机场(下图)曾是世界上最繁忙的航空枢纽之一，当时几乎所有横跨北大西洋的航班都要经停该机场补充燃料。如今，横跨北大西洋的航班不再需要经停此地。

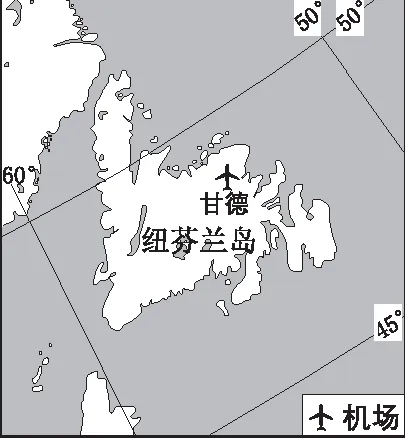
一架从甘德机场起飞的飞机以650千米/小时的速度飞行，1小时后该飞机的纬度位置可能为

( )

A．66.5°N B．60°N

C．53°N D．40°N

【解析】本题考查地球与地图中的球面距离计算。解答本题需要以下四个步骤：(1)确定飞机跨越纬度的最大值。若飞机沿经线飞行则跨越纬度范围最大，飞机飞行速度为650千米/小时，由“纬度1°所跨实际距离约110千米”可知，1小时后飞机跨越的纬度约6°。(2)确定飞机跨越纬度的最小值。若飞机沿纬线飞行则跨越纬度范围最小，由于飞机沿纬线飞行时纬度没有发生变化，因此1小时后飞机跨越的纬度为0°。(3)确定飞机跨越纬度的区间范围。飞机沿经线飞行时跨越纬度范围最大(约6°)，沿纬线飞行时跨越纬度范围最小(0°)，由题意可知，飞机的飞行方向不确定，因此飞机飞行1小时跨越纬度的区间范围是[0°，6°)。(4)确定1小时后飞机纬度位置的区间范围。由图可知，甘德机场的纬度约为48°N，由于飞机飞行1小时跨越纬度的区间范围是[0°，6°)，因此1小时后飞机纬度位置的区间范围是(42°N，54°N)。故选C项。

六、画数轴求时间法

“时区和日界线”在日常生活和国际交往中应用广泛，属于对生活有用的地理知识，既是地理教学的重点和难点，也是历年高考的高频考点。解答这部分时间计算问题难度一般比较大，需要学生具有较强的空间想象能力，但如果用画数轴的方法来求解，就会收到事半功倍的效果。数轴是一条规定了原点、方向和单位长度的直线，用画数轴的方法解答时间计算问题的好处主要有：(1)图示直观形象，使复杂的空间简单化，学生容易理解和掌握；(2)不跨越日期变更线，不需要考虑日期问题，大大的减少了学生做题出错的可能。

【例6】(2015年江苏卷·3)北京时间2015年2月19日零点钟声敲响时，某工程师在南极长城站参与了中央电视台春节联欢晚会微信抢红包活动。下图为长城站位置示意图。

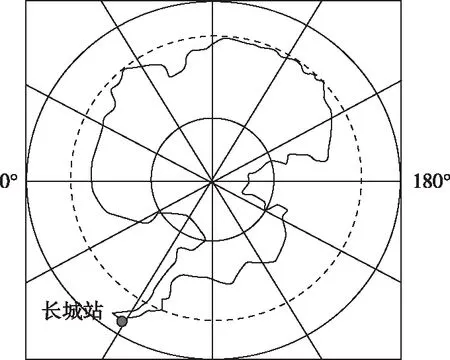
工程师微信抢红包的当地时间是

( )

A．2月18日12时 B．2月18日20时

C．2月19日4时 D．2月19日12时

【解析】本题考查地球运动的地理意义(区时计算)。由图可知，长城站位于60°W附近，当地时间是西4区区时；由题意可知，开展微信抢红包时东8区区时是2月19日0时。由东8区区时求西4区区时，可以用画数轴的方法来求解。如下图所示：(1)画数轴。画一数轴，先标注原点(即0时区)和正方向(即向右)，再标注已知时区和未知时区的位置，即东8区和西4区的位置，以原点为界东时区为正、西时区为负。(2)算距离。计算已知时区和未知时区在数轴上的距离(用S表示)，即S=东8区-西4区=12个时区，相当于数轴上8到-4之间的距离，相邻两个时区的区时相差1小时。(3)画箭头。由已知时区向未知时区画一箭头，即由东8区指向西4区，箭头指向负方向。(4)算区时。若箭头指向负方向则未知区时=已知区时-S，若箭头指向正方向则未知区时=已知区时+S，因此西4区区时=东8区区时-12小时=2月19日0时-12小时=2月18日12时。故选A项。