巧解等值线相对值的两种方法
安徽 张红军
等值线的判读是学生公认的重难点,而其中的相对值计算更是难点中的难点,亦是高考中常见的考点。关于相对值的计算,多采用公式法(n-1)d≤Δh<(n+1)d,式中n表示两者相隔或者相交的等值线条数,d表示等值距。但在考试的紧张气氛中,学生很容易忘记公式或记错公式,导致得分率降低。其实,在实际计算中,基于已有的数轴知识,以及数学中“十字相乘法”原理,巧妙地解决等值线图中相对值的计算。
【例题】图1中区域属于湿润的亚热带季风气候。
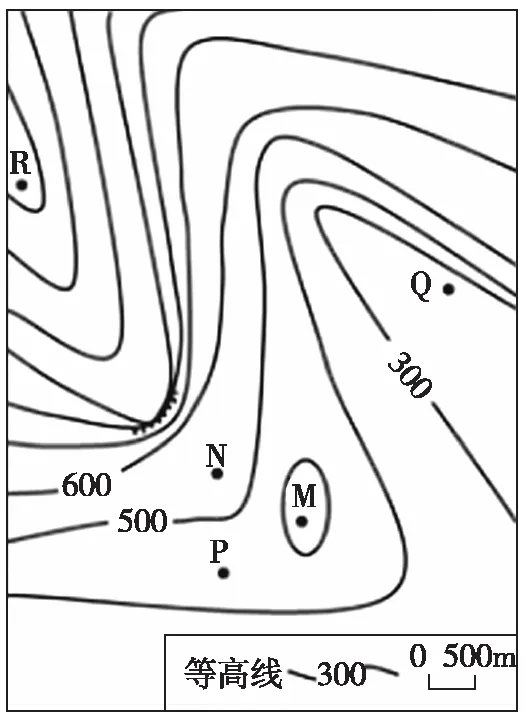
图1
广西壮族自治区南宁市第一中学)
R、Q两点的相对高度可能为
( )
A.800米 B.900米
C.1 000米 D.1 100米
一、数轴法
数轴是中学生在解决数学问题时常用的图形图像,借用数轴原理,可以直观形象地计算两地的相对值。这种方法的要领是:
第一步:读范围
分别读出所求两地的取值范围。如图1中,R地海拔取值范围是1 200~1 300米,Q地海拔取值范围是200~300米。
第二步:画数轴
画出数轴,并用粗线段分别标出R,Q两地海拔取值范围,如图2所示。
第三步:标差值
在图2数轴上直接标出两地的最大差值和最小差值。可以看出最大差值是1 300减去200,即1 100米;最小差值是1 200减去300,即900米,所以R,Q两点相对高度取值范围是900~1 100米。一般而言,不取两边值,故答案选C。
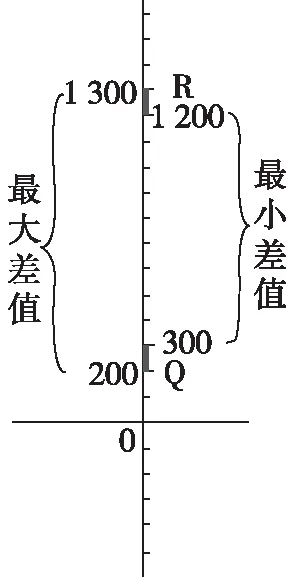
图2 数轴法
二、十字相减法
他山之“玉”可以攻“石”,借鉴中学数学中“十字相乘法”的交叉相乘原理,可以变通一下,进行交叉相减,应用到地理的相对值计算中,学生也比较容易接受。这种方法的要领是:
第一步:读范围
分别读出所求两地的取值范围。如图1中,R地海拔取值范围是1 200~1 300米,Q地海拔取值范围是200~300米。分别列式表示为1 200 第二步:十字相减 通过十字交叉相减,计算两地取值范围。为了区别显示,图3中把将要相减的两组数据分别用粗体字和斜体字表示。图中粗体字1 200和300相减值为900;斜体字1 300和200相减值为1 100。根据上述结果,可知R,Q两地相对高度取值范围是900~1 100米,故答案选C。 图3 十字相减法 需要注意的是,十字相减法中,在表示两地数值取值范围时,两地数据必须统一采用大于号(即1 300>R>1 200和300>Q>200)或小于号(即1 200 上述两种方法,不仅适用于相对高度的计算,在所有等值线图中,相对值计算都可以采用这两种方法。更为有趣的是,在不同的两幅图中,例如计算图1中R地与图5中Q地的相对高度,此时公式法显得无能为力,而数轴法和十字相减法则能轻松解决这一难题。 自某城市市中心向南、向北分别设若干站点,监测城市气温的时空分布。监测时间为8日(多云)9时到9日(晴)18时。监测结果如图4所示。 图4 ( ) A.4℃ B.12℃ C.16℃ D.18℃ 【答案】C 【解析】图示最高温为21~23℃,最低温是5~7℃,因此图示温差范围是14~18℃。一般不取两边值,所以答案C合适。 图5示意某小区域地形,图中等高距为100米,瀑布的落差为72米。 图5 ( ) A.260米 B.310米 C.360米 D.410米 【答案】C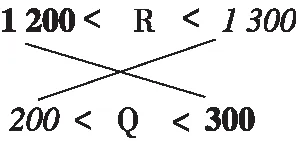
三、实战演练
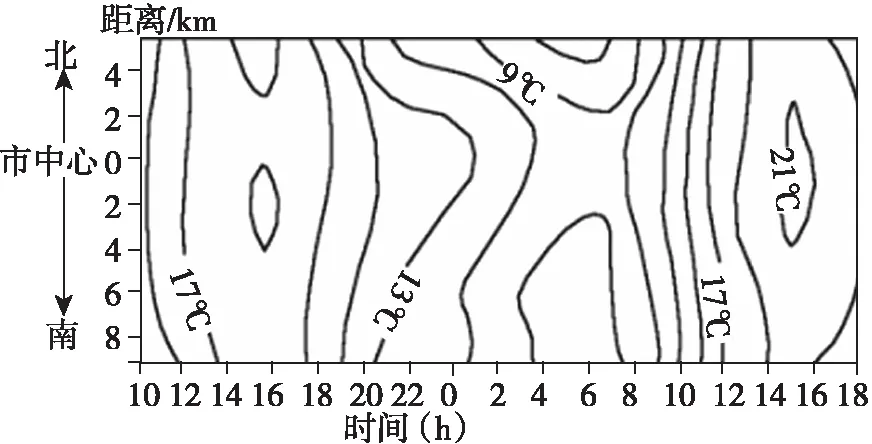
1.图示的最大温差可能是
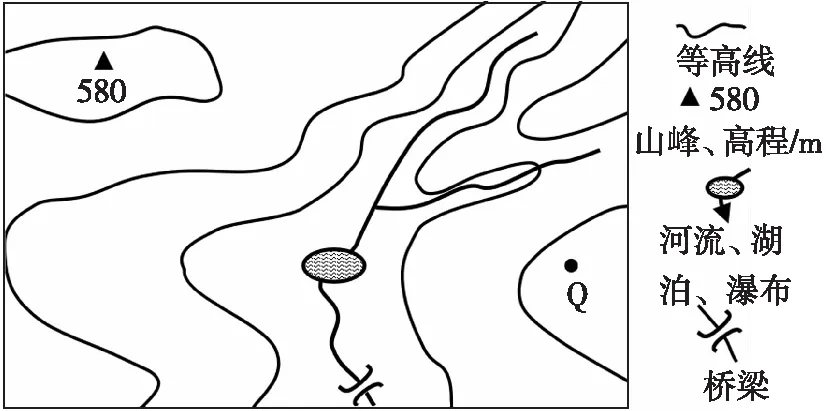
2.桥梁附近河岸与山峰的高差最接近


