基于LS-SVM方法求高阶线性ODE近似解

周水生，王保军，安亚利

西安电子科技大学 数学与统计学院，西安 710071

1 引言

在工程研究和科学计算中，大多数微分方程很难得到解析解。为了简化计算又能满足一定的实际需求，数值解的方法被应用。常用的数值方法有[1]：欧拉法，龙格-库塔法，有限差分法，打靶法以及配置法等。龙格-库塔法实质是Taylor展式的变形，函数越光滑精度越高，常用的ode45就是具有4阶精度的龙格-库塔法。虽然数值解得到广泛应用，但解的形式离散，需要经过额外的插值过程获得整个区域的解，同时为了获取更高精度的数值解，则需要不断减小步长，这些都增加了计算量。

近年，随着计算机技术的发展，一些新的智能算法被应用近似求解微分方程。这些方法基于不同的回归模型并利用优化方法求解该模型。它们克服了传统方法的缺陷，获得封闭连续可微的近似解析解。如基于遗传算法求解常微分方程[2]，神经网络方法求解微分方程[3-6]，无监督核最小平方算法求解常微分方程[7]。尽管这些方法有很好的效果，但也有一些缺点，如神经网络的方法无法确定隐藏单元的数量，并且容易陷入局部最小值而无法得到令人满意的结果。

支持向量（SVM）[8]是一种机器学习算法基于VC维理论和结构风险最小化，由Vapnik在1995年提出。该算法适用于解决小样本的分类和回归问题，具有很强的泛化能力。然而，对于大样本数据，它不得不求解一个复杂的二次规划（QP）问题而花费大量时间。Suykens[9]提出LS-SVM把不等式约束转化为等式约束，最终求解一个线性方程组，避免了求解复杂的QP问题，同时通过减少稀疏性而加快计算速度。文献[10]应用LS-SVM模型近似求解常微分方程，该方法将常微分方程问题转换为含有导数的目标优化问题，再构建LS-SVM回归模型。由于该方法对线性常微分方程有良好的性能，从而推广到求解线性时变广义系统[11]，参数估计延迟微分方程[12]，以及偏微分方程[13]。然而，该方法对于非线性微分方程，需要与其他方法相结合[10]，否则需要改进模型[14-15]，不易求解。另一方面，对于高阶线性常微分方程，该方法需要对核函数求高阶导数[10]，从而对核函数提出了更高要求。

因此，将高阶线性常微分方程转化为一阶常微分方程组，构建含有一阶导数的LS-SVM模型，从而避免对核函数求高阶导数。为了方便比较和应用，称此模型为L-LS-SVM。在求解两点边值问题时，利用线性叠加原理[16]，将边值问题转化为两个初值问题，再利用该方法求解。

2 LS-SVM回归模型

2.1 LS-SVM回归算法

对于给定的训练集{tk,yk},k=1,2,…,N，其中tk∈R，yk∈R分别为输入和输出数据。LS-SVM回归[9]的目的就是获得估计函数yˉ(t)=wTϕ(t)+b，优化模型如下：

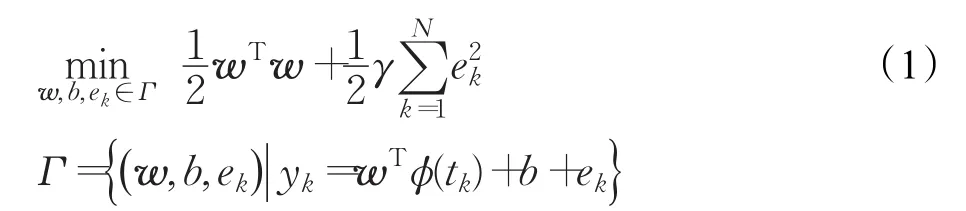
首先构造如下拉格朗日函数：

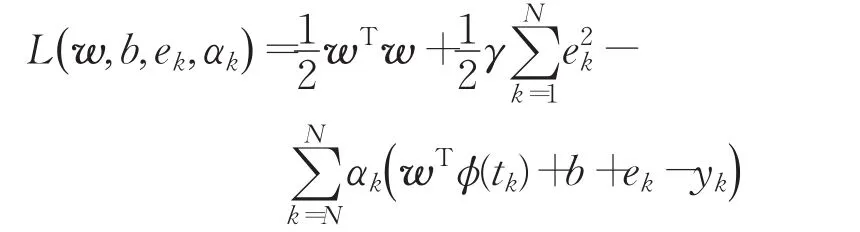
其中 αk是拉格朗日乘子，对变量 w,b,αk,ek，k=1,2,…,N求偏导获得KKT优化条件，利用该条件消去变量w和ek，整理后得到如下线性方程组：

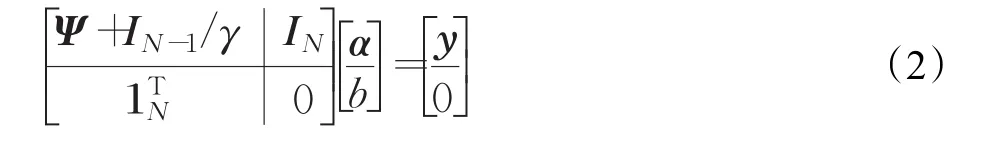
这里αk和b通过式（2）得到，K(tk,t)是核函数。

应用上述方法求解微分方程时，需要对核函数求导数[17]。根据Mercer核理论，并以高斯核函数K(x,y)=e(-(x-y)2/σ)为例给出其偏导数：

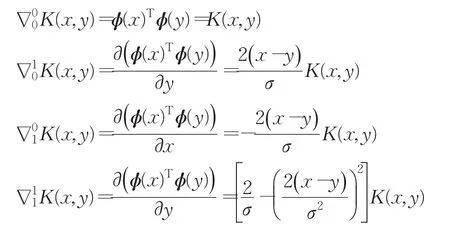
为了方便，并在后面章节中使用，对上述偏导做如下标记：

2.2 应用LS-SVM模型求解常微分方程

给出如下m阶时变系数线性常微分方程：

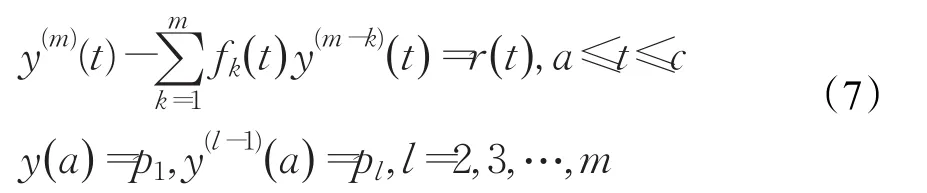
不同于一般的LS-SVM回归模型，这里没有目标值，该模型无噪音，近似解可以通过下面的优化问题获得：

3 边值问题求解

定义线性算子T：

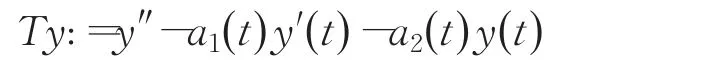
二阶线性边值问题：

由于线性微分方程具有叠加性，它的解可以由一个非齐次的特解和一个齐次的基本解组合而来。应用解析法的思想，边值问题（9）转化为两个初值问题：

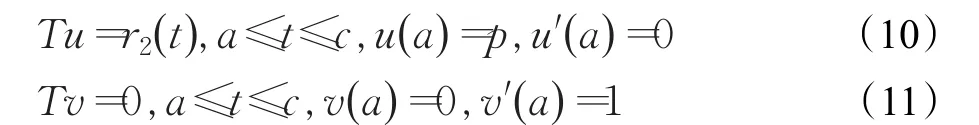
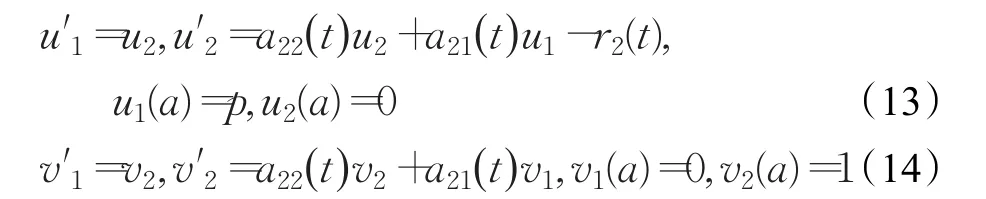
构造LS-SVM优化模型：

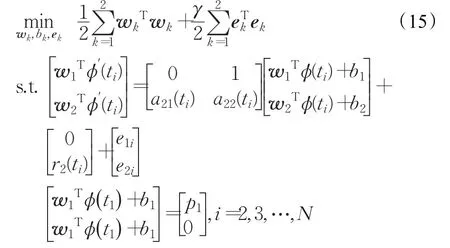
拉格朗日函数如下：

其中βk,αki是拉格朗日乘子，对变量求导得到KKT条件，之后消去变量w,ek,k=1,2，整理后得到线性方程组，详细过程可以参考下一章。利用核函数标记（4）～（6），将线性方程组写成矩阵形式：

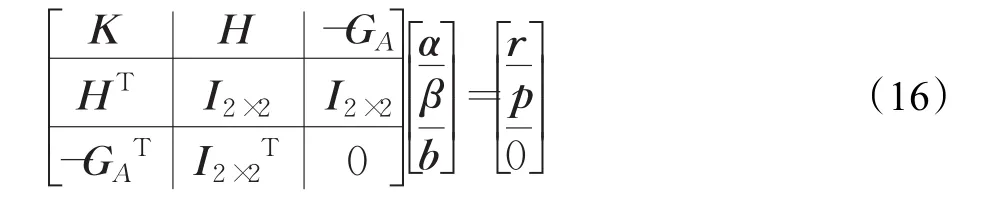
为了避免大规模求解线性方程（16），给出如下变形：

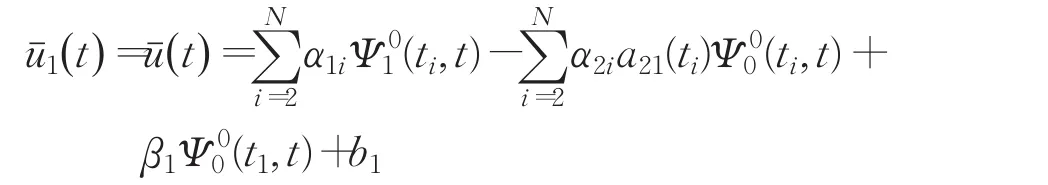
4 高阶初值常微分方程近似解

对于高阶线性常微分方程，将其转化为一阶的常微分方程组，构造LS-SVM模型求解，为了方便，称此模型L-LS-SVM。具体过程如下：

给出类似于式（7）的m阶线性时变系数常微分方程：

为了避免对核函数求高阶导数，将上述线性常微分方程转化为如下微分方程组：

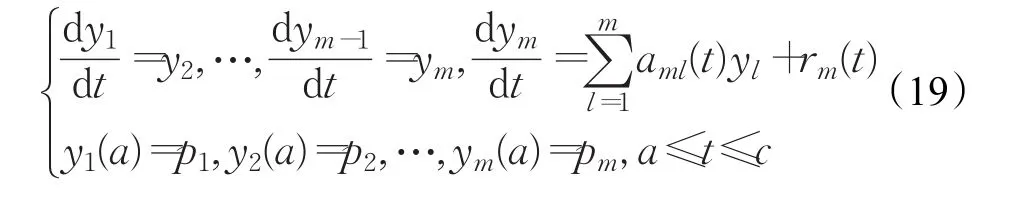
构造拉格朗日函数：

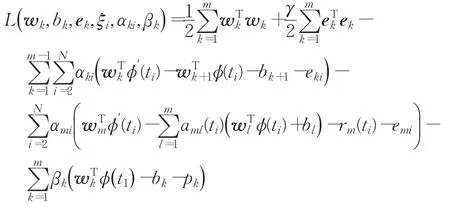
其中βk,αki是拉格朗日乘子。

对拉格朗日函数求导数，得到KKT条件如下：

之后消去变量wk,ek,k=1,2,…,m，利用核函数标记（4）～（6），整理后得到如下矩阵：

这里Q=K+HGAT+GAHT+GAGAT为实对称矩阵。把线性方程（21）分解成三个小的线性方程（22）并求解，得到问题（20）的近似解如下：

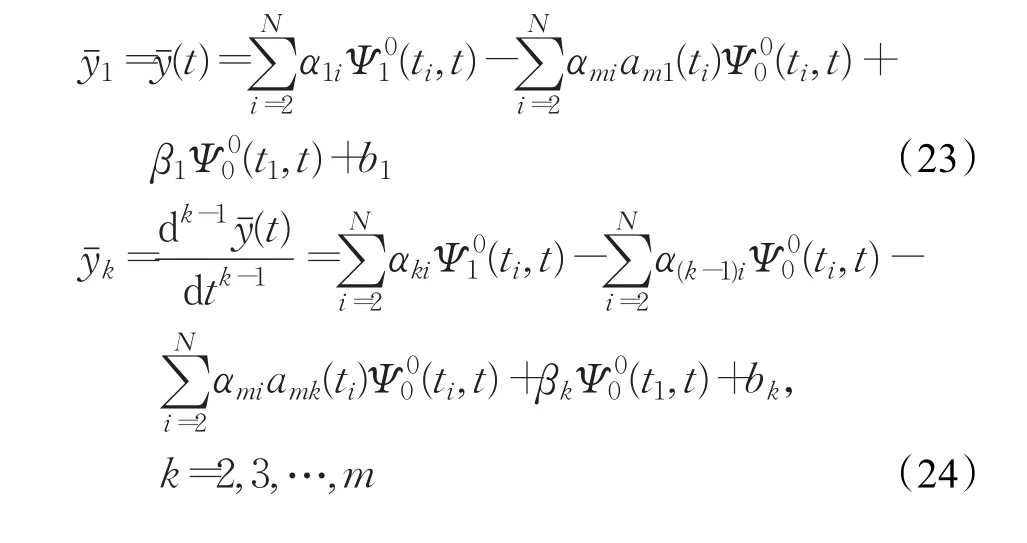
5 数值实验

通过一个边值问题和两个高阶初值问题的常微分方程来验证L-LS-SVM方法的有效性，并和文献[10]做了比较。MATLAB 2014a用于实现代码，所有计算都在Intel-core i7-4790 CPU和8.00 GB RAM的Windows 7系统上进行。

5.1 边值问题常微分方程求解

例1考虑边值问题线性常微分方程：

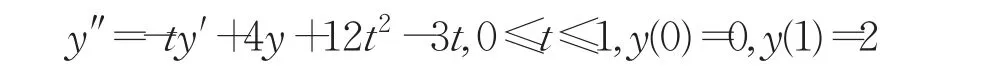
该边值问题的精确解为y(t)=t4+t，利用叠加原理，把上述边值问题转化为两个初值问题的微分方程：

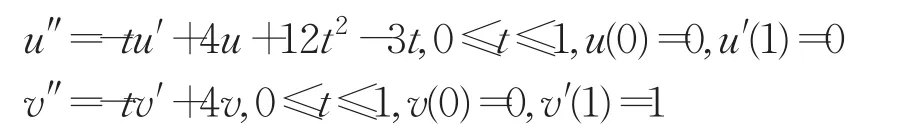
并再次转化为下面两个微分方程组：

利用LS-SVM算法分别求出这两个线性常微分方程组的近似解和，最终利用线性叠加性得到原问题的近似解

图1是例1的数值实验，在区间[0，1]内取10个等距的训练点，图1（a）为近似解和精确解实验对比曲线，图 1（b）为近似解和精确解的偏差值表1给出了训练点多少对近似解精度的影响。

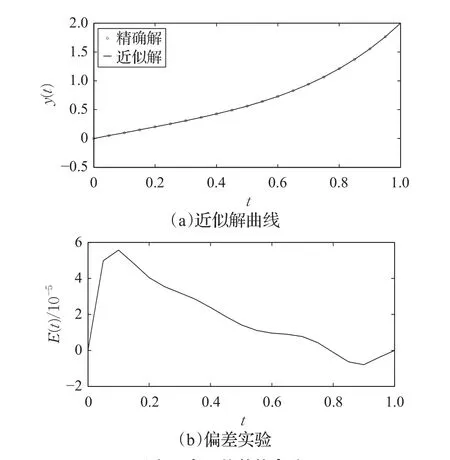
图1 例1的数值实验

5.2 高阶线性常微分方程

两个例子被给出验证L-LS-SVM方法的有效性，并和文献[10]中的方法做比较，说明两种方法得到近似解精度相当，具体结果见下面的实验和数据。

例2考虑二阶时变系数的常微分方程：

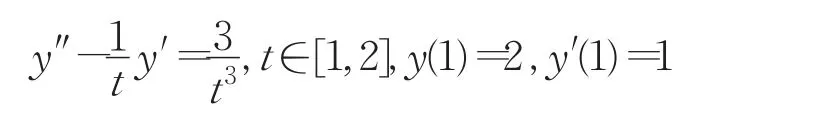
：y′1=y2,y′2=t3,y(1)=2,y′(1)=1，
3
1ty2+

图2 例2的数值实验

图2 是例2的数值实验，在区间[1，2]内取10个等距的训练点，图2（a）为近似解和精确解在区间内外对比曲线，图2（b）为近似解和精确解在区间内的偏差E(t)=。图3当γ=1010时给出了核间隔参数σ对近似解精度的影响曲线。表1给出了训练点多少对近似解精度的影响。文献[10]中的方法是目前求近似解最好的方法，因此一个详细的比较在表2中给出。

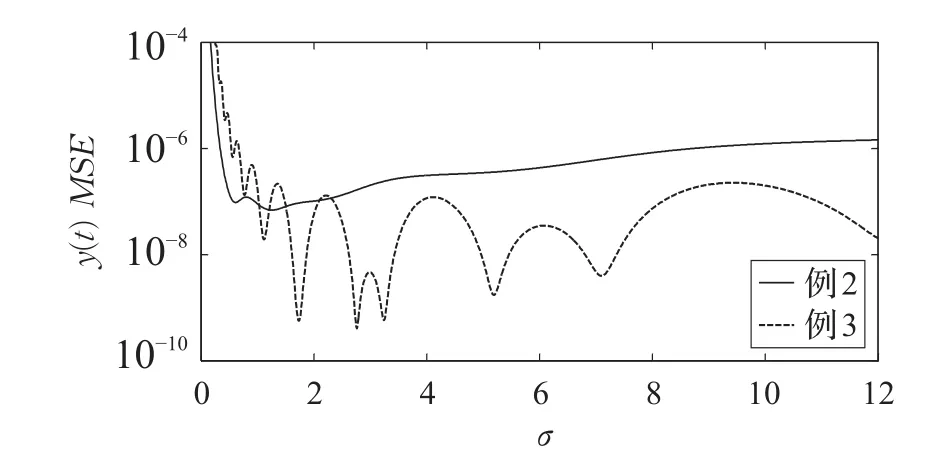
图3 初值问题的核函数间隔参数σ的敏感性实验

表1 训练点多少对y(t)的MSE影响

表2 两种方法误差比较

例3考虑三阶时变系数的常微分方程：

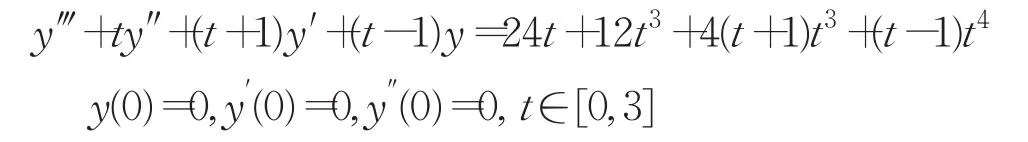
把上面的常微分方程转化为微分方程组：

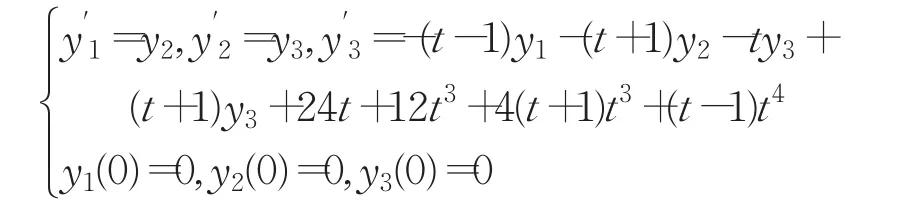
原方程的精确解析解为y(t)=t4。图3当γ=1010时给出了核间隔参数σ对近似解精度的影响曲线。

图4在区间[0，3]内取30个等距的训练点，图4（a）为近似解和精确解在区间内外对比曲线，图4（b）为近似解和精确解在区间内的偏差E(t)=y(t)-yˉ(t)，具体实验数据以及与文献[10]的比较在表2中给出。

6 结束语

对于高阶线性常微分方程，应用LS-SVM方法求解时，需要对核函数求高阶导数，为此将高阶线性常微分方程转化为一阶线性微分方程组，构建LS-SVM模型去求解该线性微分方程组，从而避免了对核函数求高阶导数。对于边值问题，利用解析的方法将它转化为两个初值问题的微分方程组求解。实验结果证明了L-LS-SVM方法的有效性，并和文献[10]中的方法做比较，说明两种方法得到近似解精度相当。将来该方法可以推广求解任意阶线性常微分方程组。

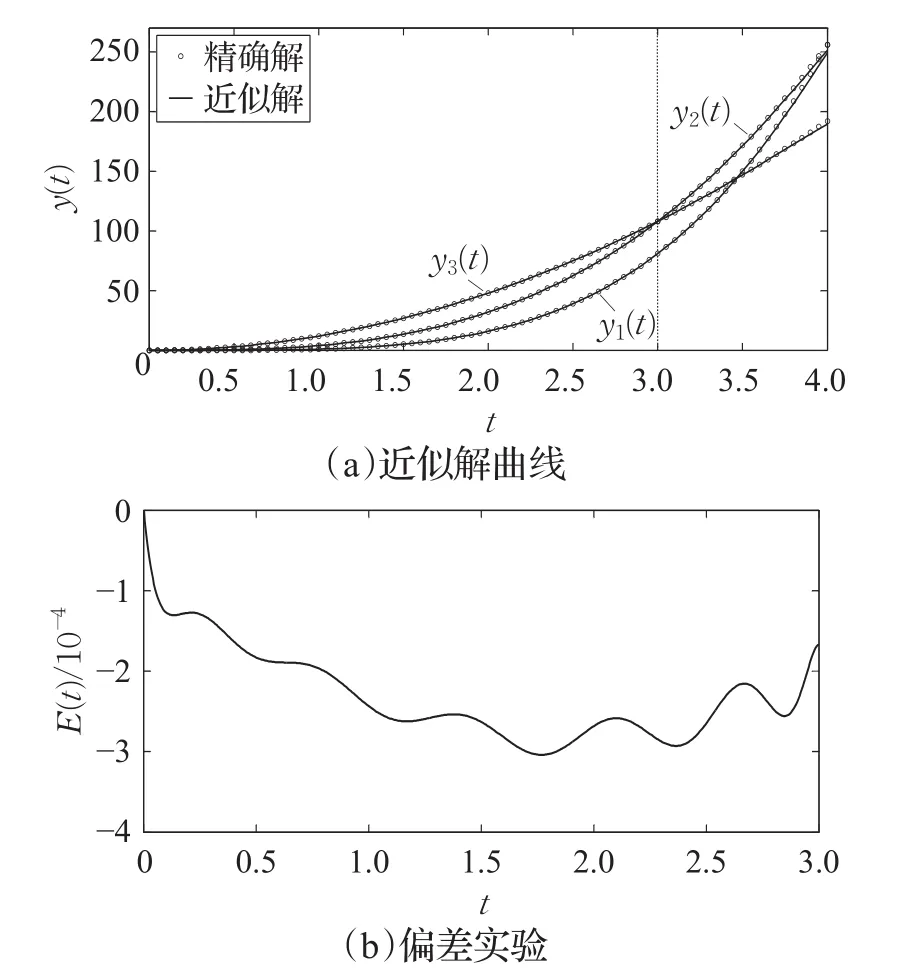
图4 例3的数值实验