在比对与自悟中提高中考复习效益
刘家良
(天津市静海区沿庄镇中学)
“都讲n遍了还是错”,这是数学教师在中考复习中常说的一句口头禅.教师认为自己讲得很清楚,学生理应听懂、会用,殊不知,对基础一般的学生来说,能有百分之六十的学生真的听懂就已经非常不容易了.那么,在中考复习的过程中,有什么方法,能使学生的思维逐步走向纵深呢?笔者认为,在比对、辨析中让学生自悟、归纳是提高中考复习效益的有效途径.
一、邻近概念的异同点、所求式子与公式结构的比对与自悟
概念是构成数学大厦的基石.在日常教学中,学生常把邻近的概念相混淆或把形式错误理解成本质,造成邻近概念的似是而非、模棱两可,直接影响了后续知识的学习.在中考复习中,让学生通过比对、辨析和自悟等活动去区分邻近概念,成为了把握概念内涵的一剂良方.公式是简化运算的工具,而学生常对那些不符合公式结构的式子也盲目套用公式,其根源是没有理清公式的结构特征,对此教师可以列举一些相似的式子让学生比对、辨析和自悟,在明确什么样的式子符合公式、什么样的式子不能套用公式的过程中达到熟悉公式结构的目的.
例1判断下列说法是否正确,正确的在括号内打“√”,错误的在括号内打“×”.
(1)实数不是有理数就是无理数.( )
(2)无限小数都是无理数.( )
(3)无理数都是无限小数.( )
(4)带根号的数都是无理数.( )
例1围绕对无理数概念的几种认识展开了比对、辨析,其中的第(2)(3)(4)小题,学生可以通过自己举例,在不同看法间展开辨析和争论,弄清无理数的内涵.学生之间的反例驳斥、辩解要比让他们死记概念的效果好,同时还可以对今后概念的学习起到示范作用.之后,再举一例加以巩固:在3.14,0.353 535 35…,0.35335333533335…,,π中,无理数有_______.
例2下列多项式乘法中,能用平方差公式计算的是___________.

这是复习平方差公式时的一道题目.明确什么样的两个二项式相乘才能使用平方差公式,是正确运用平方差公式进行计算的前提,这也是学生把握不好的地方.对此笔者设计了一组相似题,旨在让学生从“形”到“质”把握平方差公式的结构特征.此题虽然不属于难题,但是错误率还是较高的.
生1:(1)式是两个数和的积,而平方差公式是两个数的和同这两个数的差相乘,形式上就不符合,所以它不能使用平方差公式计算.
师:形式上不符合,说到点子上了.
生2:(2)式不符合平方差公式中的字母顺序,所以它不能使用平方差公式计算.(部分学生将信将疑.)
师:有不同意这种说法的吗?
生3:我不同意,这是因为.所以,变形后就符合了平方差公式的结构,所以它能用平方差公式进行计算.
师:生3通过先变形、再比对的方式判断所给式子是否符合平方差公式,看“形”还要看到“质”,从本质上看问题的思维习惯值得大家学习.
笔者边归纳、边板书:(b+a)(a-b)=(a+b)(a-b)=a2-b2;(a+b)(-b+a)=(a+b)(a-b)=a2-b2.
生4:(-a+b)(a-b)与平方差公式比较,第一个括号中a前面多了一个负号,这样,就有了三个数:-a,a,b.而平方差公式中只涉及到两个数:a,b,所以不符合公式要求.
师:生4从公式所含字母的个数上做了比对,分析到位!这个式子可以化成-(a-b)2.
生5:仿照生4的分析,(4)式中有四个数:x2,x,y,y2,因此也不符合要求.
师:生5倾听、分享生4的分析方案,这也是一种学习方法.
笔者边归纳边板书:(a+b)(a-b)=a2-b2,其中只涉及到两个字母a,b.
生6:(5)式不行,是差的积,不符合公式要求.
师:有不同的看法吗?
生7:我不同意,(5)式表面上看是差的积,但是(-a-b)=-(a+b),所以(-a-b)(a-b)=-(a+b)(a-b)=-(a2-b2),故能使用.
师:变形之后再比对,从“形”到“质”,分析得透彻.
生8:对于(6)式,开始时我认为不行,但是我从前面的分析中得到了启发,可将c2,d2分别看作公式中的字母a,b,这样就行了.
师:生8能从公式中字母a,b的广泛性上分析所给式子是否符合要求,并能在同学面前暴露自己开始时的思维缺陷,这种求实的学习品质值得大家学习.
【评析】在学生出现错误时,笔者没有马上去纠正,而是通过学生之间的相互启发、比对辨析,或变形、再比对、再判断,渐渐使公式特征浮出水面,同时悟到从“形”到“质”认识问题的重要性.这种自我比对、辨析、纠错比教师反复强调的效果要好很多.
二、一题多解的比对与自悟
学生能把自己解题的思维过程展示出来,就说明他对此类问题的理解是透彻的,教师讲的东西扎根在他心里了.在中考复习习题课上,对一道题目进行多种解答,多给学生思考、表达、比对、归纳的机会,在同中求异和异中求同中提炼出“质”的东西.虽然可能在一节课中只完成了一道题目,但是其代表了一类题目,从重“量”到重“质”的改变中让学生学会举一反三、触类旁通.

图1
例3如图1,点A,B,C在⊙O上,△ABC为等边三角形,点D为劣弧BC上一点,连接AD,BD,CD.试确定AD,BD,CD之间的数量关系,并证明你的结论.
这道题解法多样,且蕴含着辩证性思维.教师引导学生沿着观察思考、分析推理、辩证评析的路径走下去即可.
生1:在AD,BD,CD三条线段中,线段AD最长,是否会有AD=BD+CD呢?
生2:若如此,我想到了截长法和补短法.
生3:AD,BD,CD之间的数量关系为AD=BD+CD.如图2,在DA上截取DE=DB,连接BE.因为△ABC为等边三角形,所以∠ACB=∠ABC=60°,AB=CB.又因为∠BDA=∠ACB=60°,所以△DBE为等边三角形,所以BE=BD,∠DBE=60°.于是∠EBC+∠DBC=60°.又因为∠EBC+∠ABE=60°,所以∠ABE=∠DBC.所以△ABE≌△CBD(SAS),得AE=CD,即AD=BD+CD.
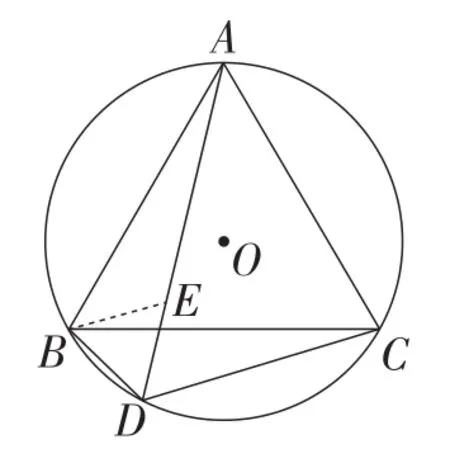
图2

图3
生4:按照生2的思路,在DA上截取DE=DC,连接CE,如图3,因为∠ADC=∠ABC=60°,所以△DEC为等边三角形,EC=DC,∠DCE=60°.可证∠ACE=∠BCD,所以△BDC≌△AEC,得AE=BD,即AD=BD+CD.
生5:生3和生4都在最长的线段上截取出一条线段等于一条较短线段,再证余下的那段等于另一条较短线段,这种方法就是教师讲解的截长法,常用于证明形如线段“a=b+c”的命题.
师:生5从生3和生4的证明过程中能感悟、提炼出典型性的方法,值得大家学习!
生6:类比截长法,能否使用补短法呢?
师:大家可以试一下.
生7:延长CD至点F,使DF=BD,连接BF,如图4.因为四边形ABDC为⊙O的内接四边形,所以∠BAC+∠BDC=180°.又因为∠BDF+∠BDC=180°,所以∠BDF=∠BAC=60°,△BDF为等边三角形,于是BF=BD,∠F=60°.证明△BDA≌ △BFC,得AD=CF,即AD=BD+CD.
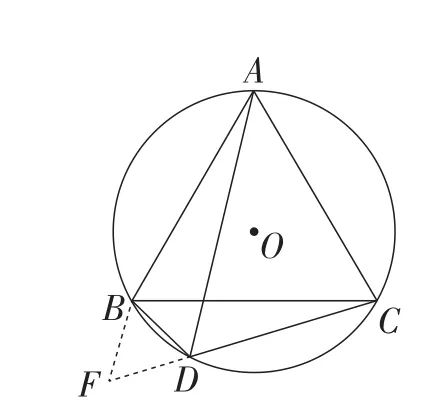
图4

图5
生8:延长BD至点F,使DF=DC,连接CF,如图5,证明△CDF为等边三角形,于是CF=CD,∠DCF=60°.证明△BCF≌△ACD,得AD=BF,即AD=BD+CD.
生9:生7和生8均采用补短法.补短法就是延长一条较短线段至某点处,使延长部分的长是另一条较短线段的长,再证总线段长等于最长的线段.
生10:无论是截取法还是补短法,其本质都是构造法.这种方法给我们提供了解决这类问题的一个通法.
师:生10从两种不同的方法中悟到了两者之间的内在联系,概括得到位.大家还有其他的想法吗?
生11:如图3,在线段AD上截取AE=BD,连接CE.先证△AEC≌△BDC,得CE=CD,∠ACE=∠BCD.再证△DEC为等边三角形即可.
师:生11从问题的另一个方面去想,这种举一反三的能力正是我们需要的.
【评析】例3始于学生的观察,前后历经了学生的观察、猜想、论证、比对、自悟、提炼和归纳等思维过程.在师生的相互启发下,高潮迭起,使学生获得解题方法的同时,又悟得数学思想,数学素养能够得到逐步提升.
三、在归类成串中展开比对与自悟
教材是复习的蓝本,教材中的题目是中考命题的“母题”,但在中考复习中有些教师往往将教材扔在一边,热衷于讲各种课外题,这种“舍本”的做法加重了学生的负担.在第一轮复习中,教师应该发挥学生的主体作用,将分散在教材各章节的关联题进行重组,归类成串,再通过学生比对、归纳、自悟,提升由此及彼、变“厚”为“薄”的高度,形成知识脉络.
有些习题虽然承载的知识看上去不同,但是其蕴涵的思想方法却是相通的.基于此,可把此类题目链接到一起,通过比较,做到异中求同,获取本质性的认识.
例4如图6,CA=CD,∠1=∠2,BC=EC,求证AB=DE.
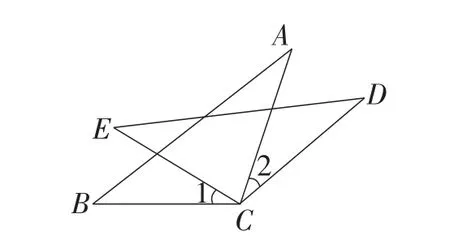
图6
此题是人教版《义务教育教科书·数学》八年级上册(以下统称“教材”)第55页第3题,这是一道先用等式性质证两个三角形的内角相等,再证其全等,得到对应边相等的题.类似地,利用等式性质证明两个三角形的内角相等,采用这种铺垫方式的题目在教材中还有一些.
链接1:如图7,△ABD,△AEC都是等边三角形,求证BE=DC.(教材第83页第12题.)
链接2:如图8,∠1=∠2,∠3=∠4,求证AC=AD.(教材第44页第4题.)
链接3:如图9,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E,AD=2.5 cm,DE=1.7 cm,求BE的长.(教材第56页第9题.)
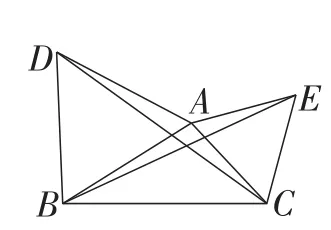
图7
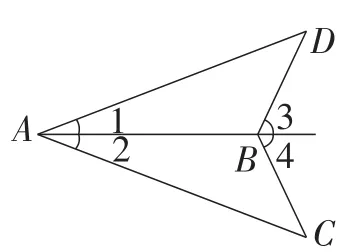
图8

图9
【评析】链接1与例4证明两个三角形内角相等的模式(等角加同一个角)是相同的,而链接3和链接4与例4的模式有别(等角的补角、同角的余角),但从例4直至链接3都是利用等式性质证明两个三角形的内角相等,“铺垫”打开了证明两个三角形全等的闸门,这一步很关键.这些题目先让学生到教材中去寻找,再让学生比对、辨析和归纳,从中找到解答这类问题的通法.
中考链接:(2016年四川·南充卷)已知△ABN和△ACM位置如图10所示,AB=AC,AD=AE,∠1=∠2.
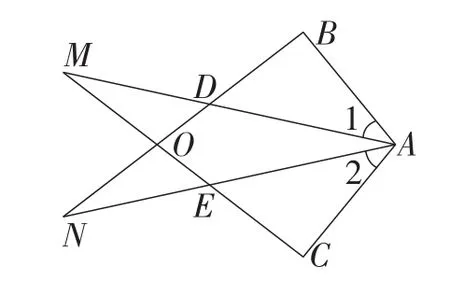
图10
(1)求证:BD=CE;
(2)求证:∠M=∠N.
这是一道与例4相仿的试题,源于教材,又有别于教材.教师要对教材有相当到位的理解,以便在总复习阶段适时引导学生在最近发展区内“跳一跳”.
【评析】在中考复习中,通过“中考链接”环节,使学生认识到中考试题的来源,从而重视对教材上题目的研究,通过对教材中关联题的重组、归类、链接,实现由“量”的训练向“类”的转变.
上述三点可适时穿插在中考复习的不同阶段,比对、辨析是“悟”的前提,这样做能使学生思维活跃、全面且严谨.求知的路上需要这种品质,这种习惯的养成,又会为我们的生活、工作带来潜移默化的影响.
——辨析“凌乱、混乱、胡乱、忙乱”

