耦合量子点系统非线性光学传感特性的应用研究

，，，，

(1.山东科技大学 电子通信与物理学院，山东 青岛 266590；2.山东省实验中学东校， 山东 济南 250109)

半导体量子点是三维受限的人工纳米微结构，具有电偶极矩大、相干时间长、器件易于集成等优点，这在光电器件设计等方面有重要的应用[1-2]。而耦合量子点分子(quantum dot molecule，QDM)是指相邻量子点通过隧穿效应耦合形成，有多能级结构，主动、灵活的电压和光学控制方法，极大地丰富了其在量子信息领域的应用[3-4]。其中量子点间的隧穿特性是量子态制备、传递和读取等量子相干调控的基础，而且研究共振隧穿效应有助于深入分析电子轨道、自旋态和价态等内禀特性以及光子/声子的吸收/辐射等外部效应，所以量子点间隧穿特性的精密测量成为当下量子传感领域的最新前沿问题之一。测量隧穿主要有电学方法和光学方法，电学方法主要分两种：一是通过对源极和漏极之间的微弱电流的精确测量反映隧穿大小[5]；另外是利用静电计靠近量子点，通过感应电荷量反映量子点的隧穿特性，属于无接触测量[3]。

光学方法具有量子态可选择性、无接触和响应快测量精确等独特优势，所以光学方法一直得到广泛关注。Stinaff等[6]较早地开展了基于光谱技术的耦合量子点隧穿特性研究。利用电压调节非对称量子点分子能级共振，空穴或者电子隧穿形成相干分子态，光谱显示了丰富的能级交叉和反交叉模式，这揭示了两个量子点的电荷隧穿特性；Govorov 等[7]利用光学吸收谱验证了量子点间隧穿耦合导致的非线性 Fano 效应。近年来，Muller等[8]利用超快光谱技术，完成了实时探测量子点分子内载流子隧穿动力学过程。2017 年 7 月，Rev. Mod. Phys.杂志综述了近年来利用量子干涉效应进行精密测量的研究，涉及原子、囚禁离子、固体自旋器件、超导器件等，进一步推进了非线性光谱技术在超高精密测量方面的应用[9]。综上所述，隧穿诱导干涉效应结合非线性光学技术，以实现对隧穿特性的精密测量方案是当前人工半导体器件以及量子信息领域值得探索的问题之一。

隧穿诱导干涉效应与外场诱导的干涉效应类似，都是由于介质的相干性导致不同跃迁路径干涉形成的干涉效应，介质对外界的光学响应受到干涉效应的影响会发生变化，如介质在相互作用中处于暗态的干涉相消现象[10]。外场诱导干涉依赖于外光场激发的相干性，由外光场强度控制；而隧穿诱导干涉主要源于点间隧穿激发的相干性，取决于介质结构。借助于非线性光学技术可以更好地了解这种干涉效应，进而了解隧穿的变化。

课题组也初步在这个方向做了一些工作，主要是借助非线性光谱技术，实现对隧穿的精密测量。具体有：利用自克尔非线性感知量子点点间隧穿变化；通过交叉克尔非线性相移探测点间隧穿特性；探究非线性吸收谱在强弱隧穿耦合下表征隧穿的变化；利用隧穿干涉实现弱信号下的高阶非线性极化率等。

图1 三能级耦合量子点分子模型Fig.1 Three-level QDM model with coupling scheme

1 自克尔非线性对隧穿的响应特性

自克尔非线性是指介质由自身光场强度引起的非线性极化率的变化。通常情况下实现强自克尔非线性需要较强的探测光强，因此实现弱场下的强自克尔非线性比较难，而Wu等[11]提出基于外场诱导相干引起的电磁感应透明(electromagnetically induced transparency,EIT)干涉效应的Raman方案，实现了强克尔非线性以及光弧子的形成。近年来，基于隧穿诱导固有相干特性引起的量子干涉效应在人工半导体材料领域受到广泛关注。孙辉等[12]基于该干涉效应实现了强克尔非线性效应。利用自克尔非线性对结构控制的隧穿特性的测量是当前材料领域和非线性光学领域新的结合点。课题组在初步的工作中，首先从简单的三能级模型出发，考察自克尔非线性的变化以及对隧穿的灵敏特性，提出基于自克尔非线性的隧穿测量方案。

基于图1所示的量子点模型，|0〉)和|1〉)分别是其中一个量子点的基态和激子态，|2〉)为另外一个量子点的基态。图中Te代表隧穿强度，ΩP是探测场拉比频率。由于量子点生长工艺的不同，两个量子点的大小不同，能级结构也就不对称，当系统未加偏压时，能级差较大，|1〉)和|2〉)态之间的隧穿很弱，基本可以忽略，整个系统可以简化为二能级模型处理。当对耦合量子点系统施加偏压以后[13]，|1〉)和|2〉)能级靠近，共振隧穿效应增强，此时量子点系统的自克尔非线性会发生变化。

利用光与物质相互作用的半经典方法处理，求解系统密度矩阵的稳态解，可以得到系统的自克尔非线性极化率

(1)

对比有无共振隧穿干涉作用的自克尔非线性，可以看出介质的自克尔非线性显著改变[14]，这也符合基于隧穿干涉实现的强自克尔非线性的方案[12]。对于隧穿的精确测量，进一步考虑随隧穿失谐的变化，在一定失谐范围内，自克尔非线性色散峰值会移动，数值模拟的灵敏度约为0.2 μeV,如图2所示。同时自克尔非线性的增益会抵消线性吸收，这也保证了探测光有较好的输出。

图2 自克尔非线性极化率实部随探测场失谐的变化[14]Fig.2 Re[χ(3)] with differentω12[14]

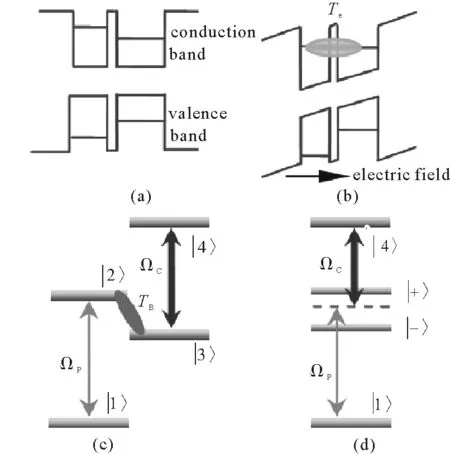
图3 耦合量子点分子能级结构Fig.3 QDM structure

2 利用增强交叉克尔非线性相移测量隧穿

交叉克尔非线性是与其他光场强度相关的三阶非线性效应。钮月萍等[15]利用双暗态相互作用，实现了增强的交叉克尔非线性。后来该课题组又利用自发辐射相干效应实现了增强的克尔非线性效应[16]，这些研究都基于原子系统中外场引起的相干性。当考虑到类原子系统中的隧穿干涉作用时，量子点间的隧穿作用耦合了两个能级，形成了相干性。在该量子点材料中，隧穿特性属于材料的内禀特性，由量子点分子的结构控制，因此称这种相干性为固有相干。这种相干性导致了不同路径跃迁的干涉效应，因此材料的光学性质会发生变化。外场诱导相干性引起克尔非线性干涉增强，同样这种固有相干性也会造成非线性光学性质的干涉效应，基于此探讨了介质的克尔非线性在隧穿探测方向的应用。

考虑图3所示的四能级耦合量子点模型，子图(a)是无偏压时的能级结构，子图(b)是加偏压后，子图(c)是激子能级及隧穿耦合方式的示意图，子图(d)是缀饰态的能级结构，探测场拉比频率ΩP和控制场拉比频率ΩC，Te代表|2〉)和|4〉)态之间的隧穿强度。若未加电压，系统退化为两个独立的二能级系统；但随着外电压的改变，点间隧穿效应增强，系统的非线性光学性质显著变化，这种变化对隧穿相当敏感[17]。求解密度矩阵方程的稳态解，可以得到系统的线性和非线性极化率分别为：

(2)

(3)

课题组从自克尔以及交叉克尔非线性这两个角度对比考察了对隧穿失谐的灵敏度，结果显示交叉克尔非线性对隧穿的响应更加明显，着重分析交叉克尔非线性对隧穿的灵敏特性，得到图4所示的结果。可以看出，在一定的控制场强度以及失谐条件下，隧穿失谐的改变不仅会移动色散曲线，而且会显著增强交叉克尔非线性色散，这会给透射谱附加额外的相移，模拟结果显示该相移量对失谐的灵敏度约为Φ=2%由于受到生长条件的限制，量子点分子的大小结构不一，很多实验中光激发的量子点分子数占比约为2%，因此在上式中引入2%的比例关系[28]。而且自克尔非线性的增益会抵消线性吸收和交叉克尔非线性吸收，这保证了测量的输出脉冲不被损耗掉。

图4 在不同隧穿失谐ω24下，交叉克尔非线性极化率的变化[17]Fig.4 Optical probe of tunneling based on enhanced cross-Kerr nonlinearity with different tunneling detuningω24[17]

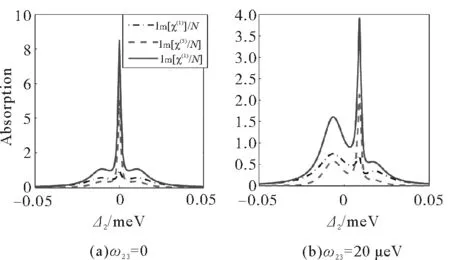
图5 线性吸收Im[χ(1)/N]，克尔非线性吸收Im[χ(3)/N]，总吸收Im[χ/N]对隧穿失谐的响应,Fig.5 Comparison of linear Im[χ(1)/N], Kerr nonlinear Im[χ(3)/N], and total absorptions Im[χ/N]

3 非线性吸收谱对隧穿的灵敏特性

EIT 和电磁诱导吸收(electromagneticall induced absorption，EIA)效应都是外场诱导相干性形成的干涉效应。Moon等[18]在原子介质的三光子干涉过程中发现了吸收增强的现象。考虑到人工半导体结构中出现固有相干的干涉作用时，耦合量子点系统的吸收谱会有类似吸收增强的效应，充分讨论了隧穿诱导吸收(tunneling induced absorption，TIA)效应，并进一步探究了吸收谱对隧穿的灵敏特性[19]。

基于图3所示的模型，隧穿诱导会形成相干性，分析干涉效应下的线性和非线性吸收谱的变化可以进一步得出隧穿的变化规律。求解密度矩阵方程的稳态解，得到线性和非线性极化率，取虚部得到线性和非线性吸收谱线。

(4)

图6 在共振以及失谐情况下，五阶非线性极化率的变化Fig.6 Real parts of fifth-order χ′(5) nonlinearities on resonance(δ2=0) and with frequency detunings (δ2=Γ1)

图7 线性吸收Im[χ(1)/N]，非线性吸收非线性增益总的增益Im[χ/N]的变化[24]Fig.7 Comparison of the linear Im[χ(1)/N], nonlinear absorptions, nonlinear

4 隧穿增强的五阶非线性极化率

通常情况下，介质的高阶极化率非常小，需要强场光实现高阶非线性效应[20]。但是弱场下的高阶非线性有更多应用，如光弧子传输[14]、量子门[21]等。实现弱场下的高阶非线性效应有两种途径，一是先实现若干弱场下的低阶非线性效应，通过这些低阶非线性的级联实现弱场下的高阶非线性[22]；另外一种方法是直接实现高阶非线性，对介质有较高的要求，介质本身需要具备大的高阶极化率。课题组基于耦合量子点系统的隧穿诱导干涉效应，实现了隧穿增强的五阶非线性效应。基于图1所示的三能级模型，当|1〉)和|2〉)之间没有隧穿作用时，模型退化为二能级系统，介质此时不具有大的高阶非线性极化率。在施加外电压的作用下，|1〉)和|2〉)之间的隧穿作用增强，且诱导形成了介质的固有相干性，不同路径跃迁的干涉效应增强了系统的高阶极化率。通过求解密度矩阵方程的稳态解，可以得到系统的五阶极化率。

模拟结果显示，共振隧穿时系统的高阶非线性极化率仍然较小，不足以满足应用要求(图6中虚线所示)。在一定的失谐条件下，系统的五阶非线性极化率极大增强(图6中实线所示)，实现了弱场下增强的高阶非线性效应。

为了保证更好地应用弱场下的高阶非线性，需要提供一个透明窗口以保证信号输出，因此进一步分析线性、三阶、五阶吸收的关系，利用三阶非线性增益抵消线性吸收，五阶吸收很弱，从而实现了整个系统的透明窗口[23]。

5 失谐增强的隧穿诱导增益谱测量点间隧穿特性

课题组又进一步探究了弱控制(信号)场下，非线性增益谱对隧穿的响应特性[24]。强控制场时，交叉克尔非线性明显比自克尔非线性大，而且对隧穿的灵敏特性也比自克尔非线性好。而在较弱的控制场下,如控制场强度等于探测场强度且共振相互作用时(ω23=Δ3=0)，介质的自克尔非线性增益和交叉克尔非线性吸收明显抵消，总吸收呈现线性吸收的特征，如图 7(a)所示。当增加隧穿失谐(ω23=0.05 meV)时，自克尔非线性增益明显变化，同时交叉克尔非线性吸收明显削弱，总吸收呈现自克尔非线性增益的特征，如图7(b)所示。而且当信号场存在失谐(Δ3=0.1 meV)时，线性吸收更弱， 总的吸收基本呈现隧穿失谐增强的非线性增益，如图 7(c)所示。更重要的是，非线性增益强度也可以很好得反映隧穿变化。模拟结果显示，失谐情况下用增益谱表征隧穿变化的探测灵敏度比共振情况下提高一个数量级，而且弱控制场失谐增强了探测灵敏度，如图 8 所示。

图8 弱场失谐增强的非线性增益谱的探测灵敏度[24]Fig.8 Detuning enhanced sensitivity S=|∂Im[G(ω)]/∂Te|[24]

6 结论

基于隧穿诱导干涉效应，利用自克尔非线性测量隧穿失谐，精确度可达0.2 μeV；利用交叉克尔非线性测量隧穿强度，探测光相移Φ≈0.28 rad/μeV；探究了非线性吸收谱随隧穿特性的变化，并分析了调制宽度、半波宽、灵敏度等表征隧穿测量的指标；探究了直接提高量子点系统高阶非线性的有效方法；提出了利用失谐增强的非线性增益谱表征隧穿变化的方案。研究成果将为隧穿的精密测量和量子传感特性的应用提供理论基础[25]。