基于响应曲面法的重介质选煤厂介质消耗控制

，， ，

(1.山东科技大学 矿业与安全工程学院，山东 青岛 266590； 2.山东科技大学 矿业工程国家级试验教学示范中心，山东 青岛 266590)

介质消耗是重介质选煤厂一项重要的技术经济指标，决定着选煤生产过程的稳定性，对选煤厂的生产成本、经济效益影响较大。重介质选煤厂介质消耗水平的控制主要从技术和管理两个角度出发。从技术角度出发的研究集中于工艺改进和设备研制两方面，如脱泥工艺[1]和末煤分选工艺[2-3]的引入和改造，以及重介质磁选机改进[4]的相关研究；从管理角度进行的研究则考虑了如何在已有的工艺和设备条件下降低重介质选煤过程的介质消耗，主要包括探究磁铁矿粉性质对介质回收效率的影响[5]，加强磁铁矿粉质量管理、设备管理[6]及悬浮液分流量、桶体液位、煤泥含量、悬浮液密度和原煤入料速度等工艺参数[7-9]的管理与控制等方面。有学者引进精益PDCA循环、精益六西格玛等方法，建立了能够有效管控关键影响因素的介质消耗管理体系[10-11]。上述研究从影响介质消耗的各种因素出发，探讨了降低和控制介质消耗的方法，但仍缺乏对各种因素、尤其是关键影响因素具体如何影响介质消耗的研究。因此，研究如何建立介质消耗与影响因素之间的关系，对影响因素的取值进行优化设置，对于提高重介质选煤厂的介质消耗管理水平尤为重要。

响应曲面法常用于探究未知系统或过程的响应输出和影响因子之间的数学模型，通过系统试验获取有效数据，并取得所希望的响应值和因子水平，达到优化响应输出的目的[12]，已成功地应用于农业、化工、医药学以及制造业等许多领域[13-20]。可通过响应曲面法设计和实施试验获取重介质选煤过程生产数据，建立介质消耗与影响因子之间的数学模型并优化输出。影响介质消耗的因素众多，将所有因素纳入试验因子的范围，可能造成不必要的浪费，故可以应用因果矩阵识别出重介质选煤过程介质消耗的显著因子[21-22]。本研究拟主要解决以下问题：识别影响重介质选煤厂介质消耗的显著因子；科学设计试验，获取建立经验模型的有效数据，建立介质消耗与其显著影响因子之间的关系；获取最优介质消耗下影响因子的参数设置方法。

1 重介质选煤厂介质消耗控制试验背景

X选煤厂的主要工艺是重介质-浮选混合工艺，其中洗选块煤的过程采用的是重介质工艺，介质消耗问题主要集中于这一阶段。该选煤厂重介质选煤过程主要包括原煤准备和原煤主再洗两大阶段，原煤准备阶段介质消耗较低，因此本研究重点放在原煤主再洗阶段的介质消耗控制上。原煤主再洗阶段采用有压给料两阶段三产品重介质旋流器进行生产，分为高密度区和低密度区两部分，分别产生产品后，进入介质回收阶段。介质回收阶段主要包括产品脱介和磁选机回收两部分，回收不彻底会导致介质附着在产品上或遗留在尾矿中形成产品介质消耗和尾矿介质消耗。因此，介质消耗主要包括产品介质消耗和尾矿介质消耗。X选煤厂原煤分选阶段的介质使用工艺流程如图1所示。试验过程中使用的原煤的基本情况如表1所示。煤的浮沉试验资料是评价煤的可选性的重要依据，这里用浮沉试验数据说明试验所用主要材料的性质。

统计该选煤厂该部分2015年整年每月的产品介质消耗和尾矿介质消耗情况，如表2所示。可知2015年年均介质消耗为1.33 kg/t，其中产品介质消耗0.80 kg/t，尾矿介质消耗0.53 kg/t。与相似工艺的选煤厂介质消耗水平(经调研得知，为0.4 kg/t左右)存在较大差距。

2 重介质选煤厂介质消耗显著影响因子分析

因果矩阵模型如图2所示[23]。在显著因子识别因果矩阵中，输出为组成介质技术损失的产品介质消耗(Y1)和磁选尾矿介质消耗(Y2)，输入为影响这两项损失的因子，aij为第i个影响因子与第j种介质消耗之间的相关性系数。识别显著影响因子之前，需要对整个介质使用工艺流程中可能影响介质消耗的因素进行全面梳理。头脑风暴法是通过将少数人召集在一起，以会议形式自由提出解决问题的大量构想的方法，是当今最具实用性的一种集体创造性地解决问题的方法[24]。因此，为确定介质消耗影响因素，分别从企业的领导层、管理层、操作层选取3名人员组成讨论小组，以头脑风暴法，从不同层面、方向和角度，根据相关技术标准和实践经验，讨论确定影响因子。根据工艺流程及介质消耗损失环节分析，最终可归纳为三大类：介质质量指标，主要包括介质真相对密度(A)、介质粒度(B)；选煤产品介质消耗控制指标，主要包括脱介水量(C)、脱介水压(D)、物料厚度(E)、合介液煤泥含量(F)；磁选尾矿介质消耗控制指标，主要包括稀介液煤泥含量(G)、磁选矿浆量(H)、稀介液磁性物含量(I)，共9个指标。按照对最终介质消耗影响产品介质消耗和尾矿介质消耗的重要程度赋值(由0至10重要程度逐渐增大)。由表2可知，产品介质消耗和尾矿介质消耗分别约占最终介质消耗的60%和40%，分别赋值8和6。然后，前述讨论小组作为评分小组，根据影响因子对产品介质消耗和尾矿介质消耗的影响程度，确定每个影响因子的相关性系数。相关性系数由六个等级构成，数字0、1、3、5、7、9分别代表“无相关”、“轻微相关”、“有一定的影响”、“有较为显著的影响”、“有显著的影响”以及“有直接而显著的影响”。最终，按照总分(总分=Σ各因子相关性系数×重要程度赋值)从大到小的顺序对影响因子进行排序，得到因果矩阵如表3所示。

图1 原煤分选阶段介质使用工艺流程图

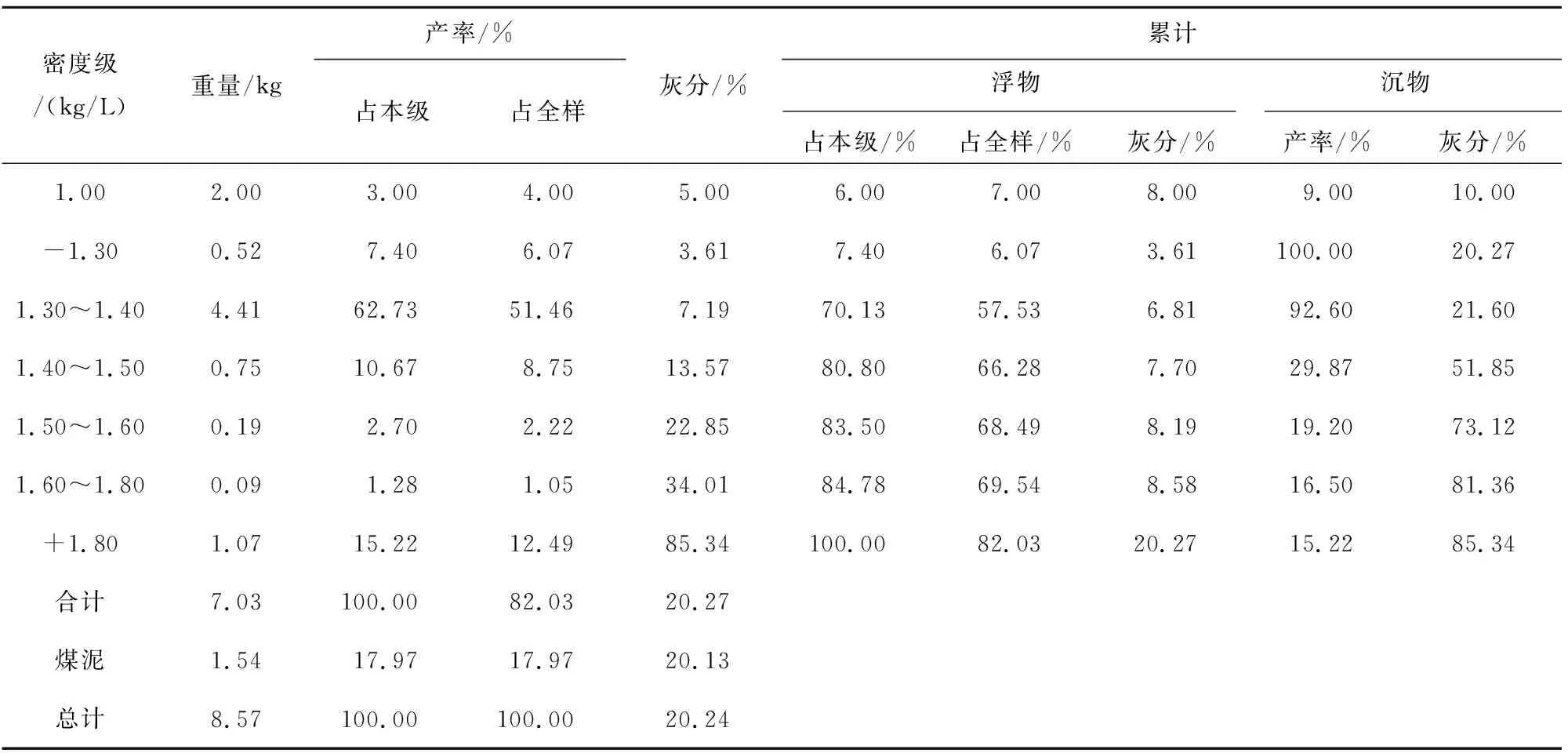
密度级/(kg/L)重量/kg产率/%占本级占全样灰分/%累计浮物沉物占本级/%占全样/%灰分/%产率/%灰分/%1.002.003.004.005.006.007.008.009.0010.00-1.300.52 7.406.073.617.406.073.61100.0020.271.30～1.404.4162.7351.467.1970.13 57.53 6.8192.6021.601.40～1.500.7510.678.7513.5780.80 66.28 7.7029.8751.851.50～1.600.192.702.2222.8583.50 68.49 8.1919.2073.121.60～1.800.09 1.281.0534.0184.78 69.54 8.5816.5081.36+1.801.07 15.2212.4985.34100.00 82.03 20.2715.2285.34合计7.03100.0082.0320.27煤泥1.5417.9717.9720.13总计8.57100.00100.0020.24

注：采样点301皮带；浮沉前煤样总质量8.60 kg；灰分21%

表2 选煤厂原煤分选阶段2015年介质消耗记录

图2 因果矩阵模型

序号影响因子介质消耗及重要程度赋值产品介质消耗(Y1)尾矿介质消耗(Y2)86得分1脱介水量(C)951022合介液煤泥含量(F)75863稀介液煤泥含量(G)57844介质真相对密度(A)55705介质粒度(B)55706稀介液磁性物含量(I)37667脱介水压(D)53588磁选矿浆量(H)17509物料厚度(E)3342

根据80/20原则，取前20%的影响因子，即排名前2名的因子作为介质消耗的显著影响因子，从表3中可知排第三位的“稀介液煤泥含量”分数仅比第二位少两分。为了提高介质消耗控制的可靠性，将“稀介液煤泥含量”也纳入研究范围。因此，该选煤厂主洗车间介质消耗的显著影响因子为脱介水量、合介液煤泥含量和稀介液煤泥含量。

3 响应曲面法

采用响应曲面分析原理，首先对筛选出的显著影响因子设计全因子试验，分析试验数据，建立以显著影响因子为自变量、介质消耗为因变量的初步模型，确定该模型是否有明显的弯曲现象。对于弯曲不明显的状况，采用最速上升(下降)法寻找能使输出接近最佳的参数取值区域，重新设定参数水平，设计试验，分析试验数据，查看弯曲情况，直到模型出现明显的弯曲，说明该模型已经接近最优值的求解，再补充部分试验，进一步丰富模型，增加弯曲项，丰富后的模型形式如式(1)所示(以2因子为例)[25]。

(1)

图3 CCD设计布点示意图(以3因子为例)

响应曲面试验设计采用中心复合设计(central composite design，CCD)，是在2水平全因子和分步试验设计的基础上发展出来的一种试验设计方法。CCD设计原理可以用立体图形说明，图形的角点为因子试验部分，中心为重复试验部分，轴点为补充试验部分。3因子CCD设计如图3所示，立方体点各点坐标皆为1或-1，这些点即第一个阶段的因子试验部分；中心点坐标为0，用于试验的重复处理；星号点，除一个自变量坐标为±α外，其余自变量均为0，在k个因子情况下，共有2k个星号点。角点和部分中心点构成了第一阶段的因子试验，轴点和另一些中心点将其扩展为2阶设计。

4 重介质选煤厂介质消耗控制试验设计、实施与分析

由于影响产品介质消耗和尾矿介质消耗的因素不同，在第2部分——介质消耗显著影响因子分析中，分别对Y1和Y2的显著影响因素进行识别。选煤厂介质消耗Y包括产品介质消耗Y1和尾矿介质消耗Y2两部分，即Y=Y1+Y2。总的介质消耗最低代表Y=Y1+Y2最小。因此，将Y作为试验的响应变量(因变量)。根据企业技术标准，经与现场技术人员确定，脱介水量、合介液煤泥含量、稀介液煤泥含量三个因子(自变量)的取值水平如表4所示。设计3因子2水平的全因子试验，同时，为满足重复性、随机性的原则，增加3个中心点试验，共运行11次试验，试验数据如表5所示。

借助MINITAB软件对试验数据进行分析，建立初步的线性模型，进行方差分析，检查是否存在明显弯曲趋势，从而决定是否到达最优区域附近。根据假设检验的原理，当置信度为95%时，C、F、G三个因子的主效应的P值分别为0.002、0.003和0.015，均小于0.05。因此，三个因子与响应变量之间存在显著的关系。方差分析结果显示，弯曲=0.045<0.05，说明模型存在明显的弯曲。

表4 影响因子参数水平设置

表5 试验数据表

图4 Y的残差图

残差检验是任一方差分析不可缺少的部分。如果模型是适合的，则残差是无定形的[26]。图4整体残差图显示，残差与拟合值之间成喇叭形(各因子残差图也显示残差与各变量之间存在明显的弯曲，因篇幅原因省略)，说明影响因子和响应之间可能存在非线性关系，为了更加精确地建立反映3因子与响应变量关系的模型，需增加试验次数，获取更加详细的数据。同时也说明现在进行的试验区域可能已经到响应变量的最佳区域附近，这时对响应变量介质消耗Y单纯拟合一阶线性方程不够，需要再补充“星号点”，构成一个序贯性响应曲面设计，拟合一个含二阶项的方程即可解决残差不符合要求的问题，并且能够更加精确地建立反映3因子与响应变量关系的模型。

因此，采用3因子中心复合序贯设计，原理如图3。总设计点共20个，包括8个立方点，立方体的中心点6个，轴点6个，轴点的中心点0个。因为是序贯设计，在上述全因子试验设计和分析中已经完成了立方点8组、中心点3组，共11组试验，所以需增加剩余的9组试验，试验计划及试验数据如表6所示，表中阴影区域为全因子设计的试验结果。

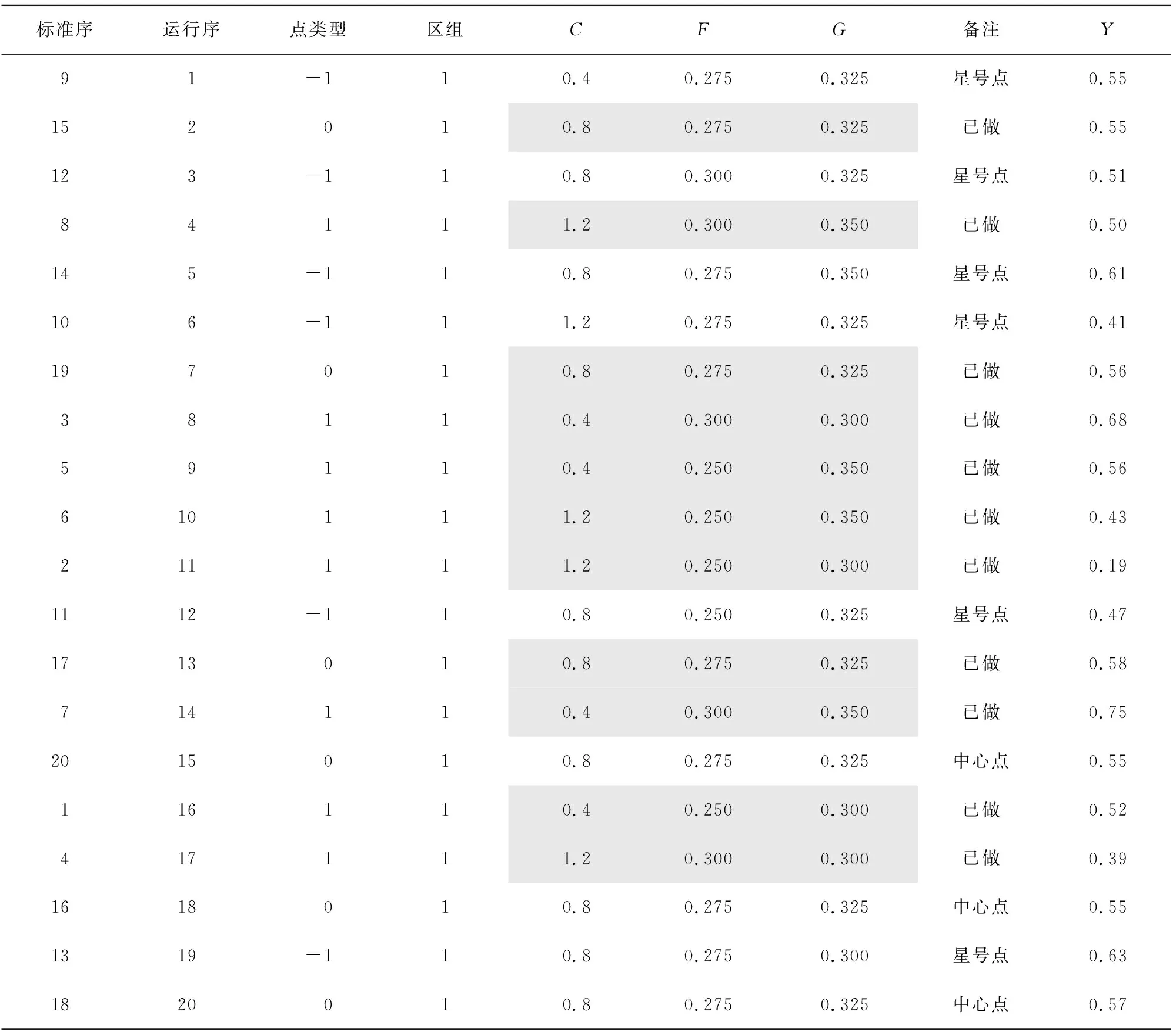
表6 第二批试验设计及数据表

借助软件，将数据代入，分析各效应的显著性。根据假设检验的原理，当置信度为95%时，C、F、G三个因子的主效应以及C因子的平方项和G因子的平方项的P值分别为0、0.001、0.014、0.036和0.029，均小于0.05，说明这几项是显著的。分析各系数显著性的同时需对模型进行检验。分析结果显示，误差占总误差的百分比R-Sq=91.56%，R-Sq(调整)=83.97%，说明该模型拟合程度比较理想；回归P=0说明回归模型是显著的，失拟P=0.127说明没有失拟情况。模型的有效性除了判断各系数的效应和整体回归的显著性，还需要对方差进行分析，由残差图5可知该模型的残差服从正态分布，且与拟合值之间具有等方差性，与顺序之间呈现随机分布关系，说明残差符合要求(各因子与残差的残差图没有呈现明显的弯曲或喇叭形，也说明残差符合要求)。

图5 整体残差图

由残差诊断可知，模型基本是好的，只存在剩余F*F、C*F、C*G、F*G几项效应不显著的问题。删除不显著效应，再次进行拟合，对得到的模型进行分析可知，各效应的显著性、回归显著性、失拟情况和残差情况均符合要求，且改进模型的方差S明显比原模型小，改进模型R-Sq与R-Sq(调整)的差值也比原模型减小，说明改进效果理想，如表7～8所示。

表7 Y的估计回归系数

注：*表示该项显著；S= 0.003 745 4；PRESS= 0.098 984 6；R-Sq= 84.41%；R-Sq(调整)= 82.14%

最终的显著影响因子和介质消耗的关系模型为：

Y=0.615C+2.64F-50.24G-0.635C2+80G2。

(2)

5 重介质选煤厂介质消耗控制参数优化

将关系模型(2)作为目标函数、因子变化范围作为综合约束条件，采用渴求函数满意度的方法求解各显著影响因子的最优取值。首先，设定响应变量Y的输出要求，经与现场讨论，结合标杆企业情况确定目标的最高值不得超过0.35 kg/t，下限设为0.1 kg/t，权重为1，重要性为1。

表8 Y的方差分析表

介质消耗属于望小型目标，越小越好，因此对于望小型的介质消耗最优参数研究采用公式(3)[27]。

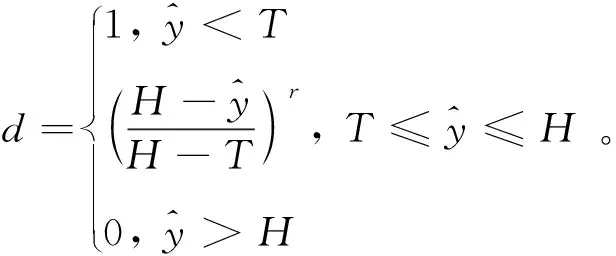
(3)

最终求得，显著因子的参数组合为：C=1.200，F=0.250，G=0.314，预测的响应Y=0.268。响应的优化图如图6所示。

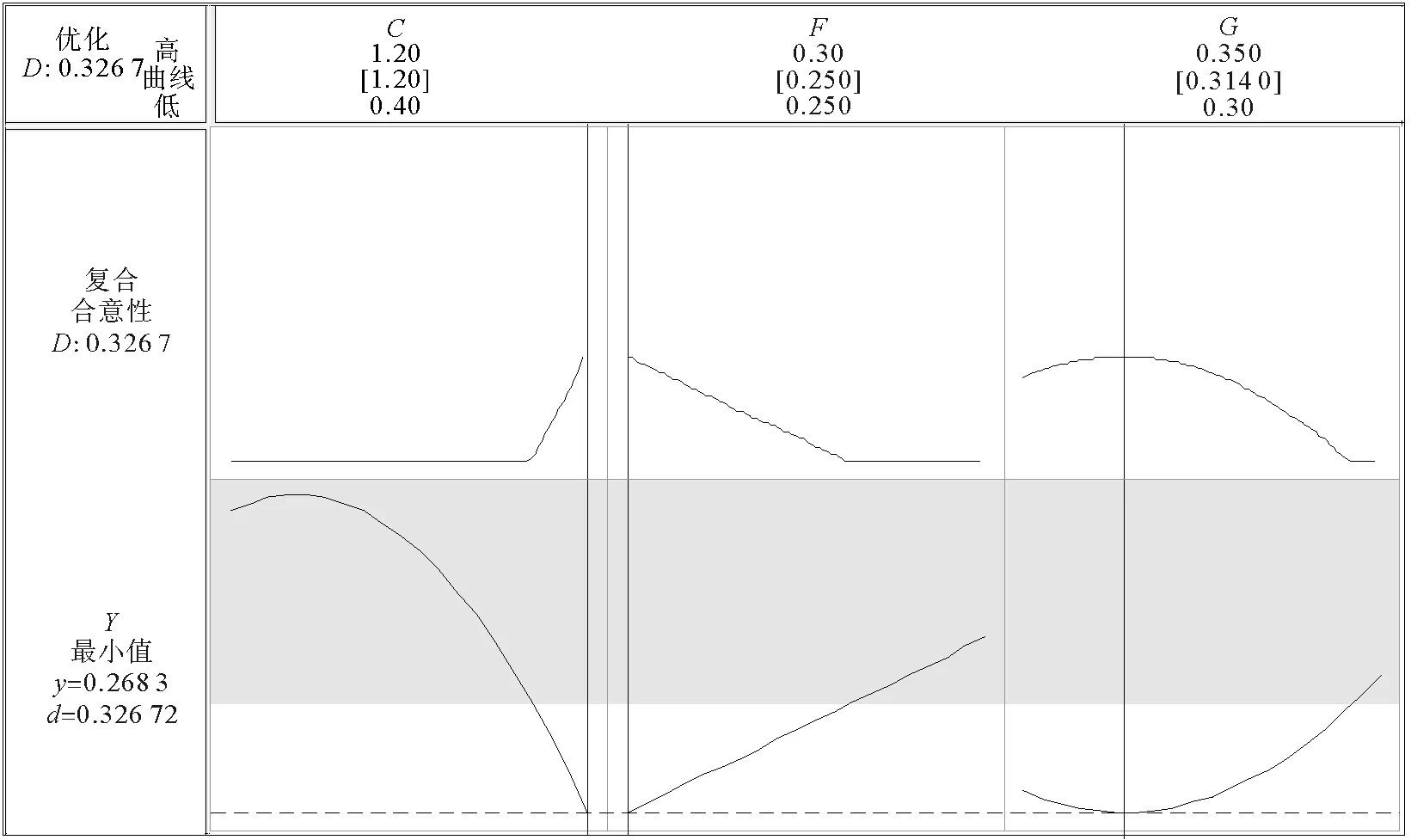
图6 响应优化图

6 重介质选煤厂介质消耗控制试验有效性分析

按照新的参数设置进行试生产，得到2016年下半年的介质消耗如表9所示，平均每月0.317 kg/t，与原来的平均介质消耗水平1.33 kg/t相比，介质消耗明显降低。按磁铁矿粉价格1 000元/t计算，每吨煤介质消耗成本降低：1 000×0.001 013=1.013(元)。

表9 2016年下半年介质消耗记录

7 结论

为实现重介质选煤厂介质消耗的精准控制，将因果矩阵和响应曲面法应用于X重介质选煤厂介质消耗控制实践中，识别出该选煤厂原煤分选部分的介质消耗显著影响因子为：脱介水量(C)、合介液煤泥含量(F)、稀介液煤泥含量(G)，建立起显著影响因子与介质消耗之间的关系模型—Y=0.615C+2.64F-50.24G-0.635C2+80G2。根据关系模型，求得显著因子取值分别为：C=1.2 MPa/m3，F=25%，G=31.4%时，Y达到最佳，最佳值为Y=0.27 kg/t。按照最优参数试生产6个月发现，介质消耗由原来的平均每月1.33 kg/t降为0.317 kg/t，吨煤介质消耗成本降低1.013元。结果表明该管控方法可用于识别重介质选煤厂介质消耗的显著影响因子，并建立显著影响因子与介质消耗之间的量化模型，从而确定影响因子的参数设置，为精确控制介质消耗提供决策依据。