多种函数模型建立解一道应用题

江苏省海门中学 (226100)

徐巧石

江苏高考一直坚持以建模为主的应用题的考查，每年各市的模拟试题中都会出现一些好的应用题,它们能够激发学生的发散思维，提高学生数学建模与数学运算的能力.本文就一道应用题，建立不同的函数模型解决其最优解问题.

图1

一、问题呈现

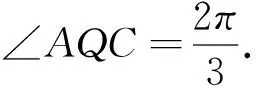
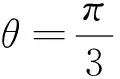
(2)当∠OPQ越大，游客在观赏亭P处的观赏效果越佳，求游客在观赏亭P处的观赏效果最佳时，角θ的正弦值.

二、多角度思考解决方案

(1)略

(2)方案一：余弦定理构造角的余弦函数，基本不等式处理最小值，等号成立确定θ值.

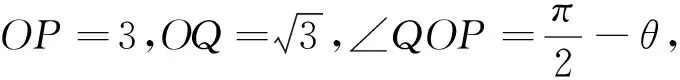
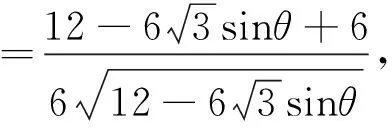
方案二：余弦定理构造角的余弦函数，基本不等式处理最小值，余弦定理确定θ值.

方案三：(正弦定理构造角的正切函数，求导处理最大值，导数为0确定θ值).

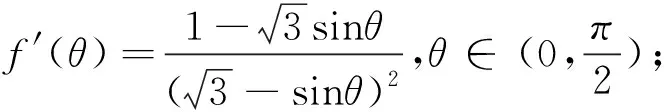
方案四：正弦定理构造角的正弦函数，基本不等式确定最大值，等号成立确定θ值.

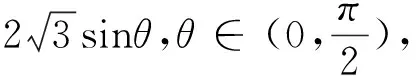
方案五：正弦定理构造角的正弦函数，三角有界性确定最大值，三角恒等变换确定θ值.

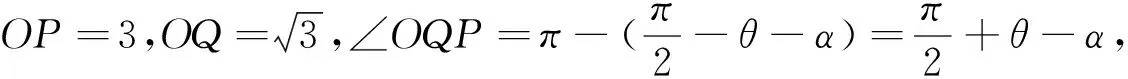
方案六：正弦定理构造角的正弦函数，三角有界性确定最大值，几何关系确定θ值.

三、两点启示

2017年新的课程标准中提出的数学学科的核心素养中包括数学建模.数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.数学模型搭建了数学与外部世界联系的桥梁，是数学应用的重要形式.江苏高考一直以应用题的形式来考查学生数学建模与数学运算的能力.在平常的教学中我们更要注意培养学生

1.打牢基础知识，透析问题本源

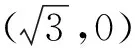
2.加强运算训练，提高抗压水平

数学课程标准指出“数学运算是解决数学问题的基本手段.数学运算是演绎推理，是计算机解决问题的基础.通过高中数学课程的学习，学生能进一步发展数学运算能力；有效借助运算方法解决实际问题；通过运算促进数学思维发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神.”

因此在教学过程中要注重学生运算能力的培养，如方案四中很多学生都建立了这个函数，但是在求最值的过程中都半路夭折，只有少数坚持到底.所以平常可以训练一些运算量大的题目，提升学生的运算能力，增强抗压的水平.