一道高考理科数学题推广的进一步研究
陕西安康学院数学与统计学院 (725000)
赵临龙
2012年安徽省高考理科数学20题如下:

图1

(Ⅰ)如果点Q的坐标是(4,4),求此时椭圆C的方程;
(Ⅱ)证明:直线PQ与椭圆C只有一个交点.
文[1-2]将椭圆的切线扩展为2条,给出新结论,文[3]将椭圆的焦点扩展为2个,又给出新结论.文[4]将椭圆推广到双曲线,给出相关结论.但在这些结论中,有些是本题的内在特性,而有些并非是本题的内在特性,甚至有些结论是错误的.
文[5]对出现的问题进行讨论,但遗憾是文[5]可能是由于版面紧张,只有讨论过程而没有结论.现结合相关问题,将椭圆推广到中心二次曲线,给出相关结论,以完善相关结论.值得注意是,要揭示本题的内在属性,需要借助射影几何的知识.
1 知识准备
定义[6]如图2.过点P(x0,y0)引二次曲线Γ:
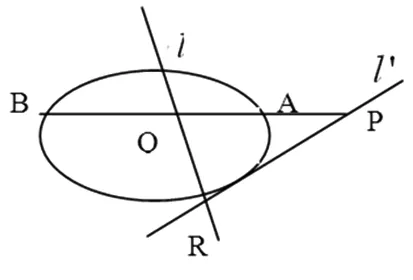
图2
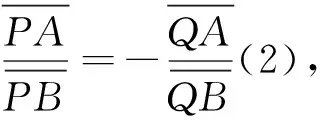
引理1[5]若点P关于二次曲线Γ的极线为l,则l上一点Q关于二次曲线Γ的极线l'必过点P.
引理2[5]两极点P、Q对应极线分别是l和l',则l和l'的交点R关于二次曲线Γ的极线为直线PQ.
推论1 中心曲线Γ的焦点关于Γ的极线是其对应准线.
2 命题讨论

图3
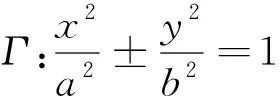
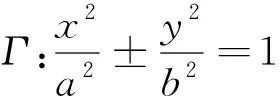
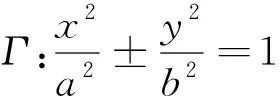
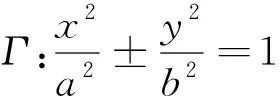

图4
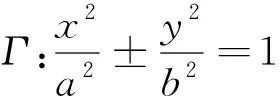
证明:如图,两切点A、B的极线AQ、BQ相交于极点Q,则极点Q的极线为AB.由于极点Q在焦点F2一侧的准线上,则极线AB必过焦点F2.由定理1,得到QF2⊥AB.
推论2 过中心曲线Γ相应于焦点F2一侧的准线上任意一点Q与Γ的焦点F2的连线垂直于点Q关于Γ的极线.

图5

证明:如图,由于极点Q1的极线为AB,极点F2的极线为其准线,且两极线交于点Q2,则极点Q2的极线为Q1F,于是由推论,得到:Q2F2⊥Q1F2.同理,Q1F1⊥Q2F1,则有结论.
推论3 过中心曲线Γ相应于焦点F1、F2的准线上的点Q1、Q2关于Γ的极线分别为Q2F1、Q1F2,则四点Q1、Q2,F1、F2在以Q1Q2为直径的圆上.
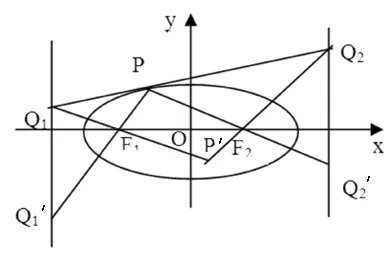
图6
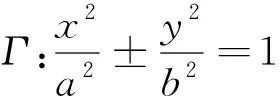
证明:如图,点Q1、Q2关于中心曲线Γ的两极线PF1、PF2交于Γ于点P,于是以两极线PF1、PF2交点P为极点关于中心曲线Γ的极线必过点Q1、Q2,即Q1、P、Q2三点共线.由定理2,知直线Q1PQ2切中心曲线Γ于点P.现设当点P是中心曲线Γ的切线Q1PQ2时,则Q1′是极点F1、Q1分别对应准线Q1Q1′、


