例谈缩小角范围的常用策略
2018-12-04 07:32:18福建省莆田第二中学351100
中学数学研究(江西) 2018年11期
福建省莆田第二中学 (351100)
蔡海涛
在三角恒等变换中,解决求值或求角问题时,常常会出现解出两个或两个以上答案的情况.学生在遇到这类问题时,往往无所适从,不懂得从已知中寻找条件,或挖掘隐含条件,去缩小角的范围,然后进行合理的取舍,从而导致产生增解.本文例谈几种缩小角的范围的常用策略,以期抛砖引玉.
根据三角函数值的符号缩小角的范围
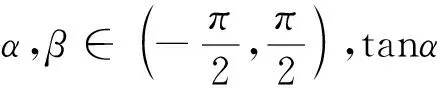

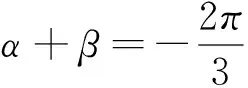
二、利用三角函数的单调性缩小角的范围
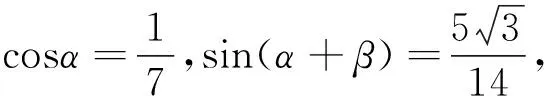
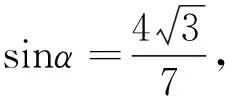

利用三角函数的单调性,可比较已知角与待求角的大小关系或比较已知角、待求角与特殊角的大小关系,从而对角的范围进行缩小.
三、借助单位圆的三角函数线缩小角的范围
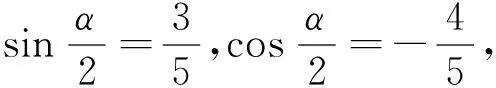

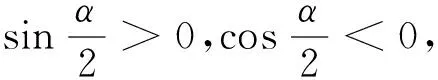
四、挖掘隐含条件缩小角的范围

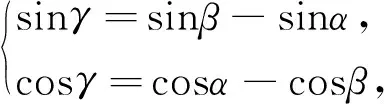
评析:本题容易忽略由sinα+sinγ=sinβ得到sinβ>sinα,从而得到β>α这个隐含条件,故在解决给值求角时,要充分挖掘隐含条件,尽可能缩小角的范围.
例5 在△ABC中,若3sinA+4cosB=6,3cosA+4sinB=1,求角C的大小.
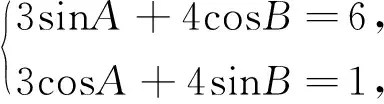
评析:一般说来,在解决三角求值或求角问题出现两个答案时,常常要进行检验,挖掘隐含条件进行合理的取舍.
由以上各例可见,正确估算角的范围在三角解题中十分重要,只有在解题中多“留个心眼”,合理运用缩小角的范围的策略,才能在三角解题中得心应手,游刃有余!
猜你喜欢
舰船科学技术(2022年20期)2022-11-28 08:22:56
音乐教育与创作(2022年6期)2022-10-11 01:14:20
中学生数理化(高中版.高考数学)(2021年11期)2021-12-21 05:34:28
新世纪智能(数学备考)(2021年11期)2021-03-08 01:08:12
新世纪智能(数学备考)(2020年11期)2021-01-04 00:38:24
电子制作(2019年19期)2019-11-23 08:41:52
中学生数理化·高一版(2019年9期)2019-10-12 07:25:44
消费导刊(2017年24期)2018-01-31 01:28:30
电子制作(2016年19期)2016-08-24 07:50:04
数学物理学报(2014年3期)2014-03-11 18:34:20

