构建数学模型提高中学生创新意识
安徽省六安市皋城中学 (237000)
李 刚
创新是引领发展的第一动力.抓创新就是抓发展,谋创新就是谋未来.党的十八大以来,以习近平同志为核心的党中央把创新摆在国家发展全局的核心位置,围绕实施创新驱动发展战略,加快推进以科技创新为核心的全面创新.在基础教育阶段,中学数学应该承担起培养学生创新意识的责任,为社会所需要的创新型人才提供支持.
《义务教育数学课程标准》(2011)第二部分课程目标提出:通过义务教育阶段的数学学习,学生能“了解数学价值,提高学习数学的兴趣,增强学好数学的信心,养成良好的学习习惯,具有初步的创新意识和科学态度”.
数学是研究事物之间和事物内部空间形式与数量变化规律的科学,在中学数学教学中,数学模型思想的渗透,数学方法的掌握,数学思维的形成,在实际中往往只有通过大量做题来实现.要改变这样的现状,最有效的途径就是通过适当的方法,培养学生的创新思维.下面就如何在中学数学的课堂中通过数学模型的方法提高中学生的创新思维进行一些简单的探讨.
一、从普通问题入手,培养创新思维
生活中,很多会品茶的人品茶的时候都讲究一个氛围,一杯清茶,围着不疾不徐的风雅琴韵,这就是氛围.在中学数学教学中创设适当的情景氛围,比如,利用现代化的多媒体设备,他能巧妙地融音乐、图片、动作表情于一体,教师可以充分运用录像、投影、幻灯片,音响等设置情境氛围进行教学,能最大程度的激发学生学习的兴趣,使他们乐于投入到数学学习中来!
比如,抓住中学生对做游戏比较感兴趣的贪玩心理,在讲解“相反数”一节时,如何生动形象的让学生理解相反数的概念,可以在课堂上做个小游戏,让一名同学站在讲台上,面向大家,然后喊口令“向后转”,分别转一次,转两次,问这位同学每次所面对的方向如何?学生自然很容易就能明白1,-1,-(-1)这一类概念的区别与联系.
再如,在找规律中,有这样一组数:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
……
从中不难得出前n个奇数的和为n2这个结论,对于很多学生来说这是一个悬念,它可以从几何图形上面得到进一步的直观的解释.

图1
一个方块的面积为1,增加3个方块,则变为一个2×2的方块,它的面积为4;再增加5个方块,则变成一个3×3的方块,它的面积为9,依此类推.如图1.
该例说明,我们在训练学生的解题思路和方法时,要有选择,有控制地给学生提一些典型的、特殊的思想和方法,循序渐进地开拓学生的解题视野,使他们在思想方法上,在寻求解决问题的途径中能够做到前后知识互补、互相促进,克服学习中的畏难情绪,培养自强不息和积极向上的学习精神,让学生视野远大,心胸开阔,思维活跃,学习主动,才能逐步达到学习目的.
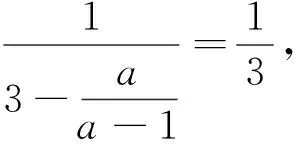
分析:求解的常规思路把a用任一数替换,验算等式是否成立.
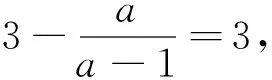
培养中学生数学创新思维能力的方法很多,但必须做到科学、适度,而且要有难度,必须在学生的“最近发展区”内.采用数学模型的思想方法,对教师的教学设计水平和学生的学习指导有帮助,对学生的影响很大.影响可以分为两个方面:一方面,影响学生的学习过程,改变传统的学习方式,可以引起学生的学习兴趣,激发学生对数学问题的应用探索和求知欲,在数学建模中建立创新意识和创新能力.另一方面培养和提高学生的合作精神和团队意识,培养学生自律的良好品质,这些对于后续课程的学习和独立研究,都有很大的好处,最后提高学生的可持续发展,培养学生适应现代社会要求的素养.
二、构建数学模型,提高创新意识
《义务教育数学课程标准》(2011)指出:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径.建立和求解模型的过程包括,从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数学关系和变化规律,求出结果并讨论结果的意义.这些内容的学习有助于学生初步形成模型思想,提高学习数学的兴趣和应用意识.
数学模型是人们为了得到一个特殊的研究目标,按照目标的独特内涵,建立一种具有抽象性、简化性和趣味性的数学结构,即现实生活中的数学问题在研究的过程中用数学的方式构造出来.数学建模是假设简化现实生活中问题的背景和所依据的数学模型的目的,找出未知数和相关参数之间的关系,并用字母表示未知数求解;采用相应的物理或其他规则,使用数学问题变量建立数学公式和参数列表即确立数学模型计算的解决方案,解答数学问题.用这个答案解释生活中的原数学问题,最后把上述结果用实际情况来验证,并用来处理多周期的实际问题和研究问题的深化过程.
利用数学建模,一方面可以引导学生积极的去探索数学问题和激发他们的求知欲,提高他们学习数学的兴趣;另一方面培养和提高学生的合作精神和团队意识,培养学生良好的品质,如严谨和自律等,这为后续课程的学习和自主学习,都有很大的好处.
数学模型的建立过程就是数学模型的本质,即数学知识应用到实际问题转化成概括性的逻辑思维的数学关系的变化,然后处理所有相应的数学模型,形成之间的数学关系.数学建模过程可以表示在以下五个方面:
分析问题过程:了解问题的实际背景材料的性质,分析和找出问题的目的.
问题的假设化简:把影响研究目标的必要成分找出来,把次要成分忽略掉,这样杂乱无章的数学问题就被概括成具体问题.

↓

数学模型的建立:数学模型是要建立在原先假设的基础上,通过运用适当的数学工具和数学知识来刻画变量之间的数量关系,因此得到相应的数量结构.
求解数学模型:根据数学模型分析,用数学方法和计算机程序来求解数学建模.
模型的验证分析:检验模型是不是与实际相符合,并对它做出诠释.
(一)函数模型
在解决实际问题时,存在函数关系的数学问题时可以建立函数模型.
例3 某家服装店进了一批衣服,一件衣服的进价为48元,为了获得更多的利润,售价要高于进价,经过观察可得,当每一件的价格是60元时,每月有180件衣服售出,当每一件衣服价格是75元时,每月有105件衣服售出.如果商店衣服不积压,忽略其他因素,则在售价为多少时,所获利润最大?最大是多少.
分析:题设中并没有指出售价与销售量之间的函数关系,只是告诉大家在两种不同价格下的销售量.所以,教师可以通过带领学生观察实际生活中的真实销售问题,分析得到:售价越高,销售量越低的规律,构建简单一次函数的数学模型,假设售价x与销售量y之间的函数关系为y=kx+b的一次函数形式.
解:由题意得,设这个函数的解析式是y=kx+b,则有
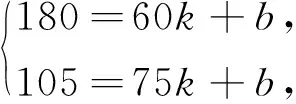
函数模型常用来解决利润,增长率,路程,面积的大小等问题.这些问题可以通过日常的真实体会,得到一般性的规律,然后根据这一规律,构建适当的数学模型进行求解.当然,上述问题,除了引导学生思考简单的一次函数模型之外,还可以启发学生,是否还有其他的模型(不是一次函数模型)可以刻画“售价越高,销售量越低”的规律呢?在相应的模型下,价格和最大利润分别又是多少呢?相信在学生中会有很多具有新意的讨论.除此之外,还可以进一步启发学生:实际情况中,积压是很常见的现象,如果出现了积压,那么售价又该如何决策,才能达到利润最大呢?
(二)不等式(组)模型
我们要解决存在不等关系的实际问题就得使用不等式的思想去解决,所以我们要建立不等式(组)模型.
例4 某校组织学生参加郊游,需要在某宾馆住宿一晚,假如每个房间住4人,那么就有20人住不下;一样的房间,假如一间房住8人,那么还有一间不满也不空.请问:这所学校有多少学生参加春游?
分析:启发学生,真实的情况中,房间的个数必须是整数.
解:设他们需要x间房,由题意得
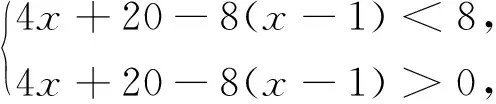
解得5 不等式(组)模型可以用于产量的估算,决定是否投资,亏盈的分析,价格的核对等,在实际经济生活中广泛应用. 在我们解决实际问题中,遇到用方程性质解决的问题时,可根据实际问题的已知条件,设出合适的未知数,找出相等的关系,最后检验算出的结果是否符合题意. 例5 2019年的新年快到了,某玩具厂要生产一批有猪形状的新年吉祥物甲,乙两种,该玩具厂主要用A,B两种原料.已知需要用A种原料和B种原料分别为4盒和3盒才能生产一套甲吉祥物,需要用A种原料和B种原料分别为5盒和10盒才能生产一套乙吉祥物,玩具厂购进20000盒A原料和30000盒B原料.如果原料没有剩余,求这个玩具厂生产两种吉祥物各多少套? 分析:在解决实际问题中应用广泛,例如人员调配,工程实施,产品购销等,都可以建立方程(组)模型解决. 解:设生产甲种吉祥物x套,乙种吉祥物y套,由题意得 从而,如果原料没有剩余,则这个玩具厂生甲乙两种吉祥物分别为2000套和2400套. 教师在带领学生分析问题的同时,也要启发学生,现实生产中,原料有没有剩余或者短缺?如果剩余了或者短缺了,我们又应该如何处理问题?诸如此类的问题,可以一步一步带领学生构建更加贴近生活的数学模型,激发学生学习的兴趣.在整个过程中,我们也会发现学生会提出一些非常具有创意的想法.如果能够合理加以引导,学生的思路远比我们想象的还要具有创意. 总之,数学模型在解决实际问题中的使用,不仅能够理论联系实际,而且学生的学习兴趣在解决问题的过程中也随之提高,从而提高学生掌握数学知识的能力和理解,还会更好的把数学思想方法用到解题过程中去,加固学生的数学知识结构.解题的过程中,学生敢于质疑,开阔自己的求异思维,独自去思考和探索,去提出自己的新观点,新思路,新方法.同时可以加深对探索和创新思维的培养,发展学生自主探究能力,从而提高学生的创新能力.(三)方程(组)模型