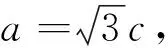数学课堂教学的厚度、宽度和长度
——《正弦、余弦定理习题课》的教学设计与感悟
江苏省无锡市立人高级中学 (214161)
郑宝生 赵 勤
作为数学课的一种重要形式——习题课,有些教师把它上成解题训练课,大搞题海战术以多取胜;也有些教师搞题型分类课,让学生见到什么题型就用什么解法,固化学生的思维.我们有必要重温一下普通高中《数学课程标准》:“数学课程要讲逻辑推理,更要讲道理,通过典型例子的分析和学生自主探索活动,使学生理解数学概念、结论逐步形成的过程,体会蕴含在其中的思想方法,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态.”反思我们的习题课教学,如何在解题中讲道理、夯实基础?如何设计适合学生的探究活动、拓展知识、开阔思维?如何让学生在归纳总结中提炼思想,体验成功乐趣,发展理性思维?本文以《正弦、余弦定理习题课》为例,谈谈对这一问题的认识.
一、习题课例
(一)目标解析
通过学生练习回忆正弦定理和余弦定理,体会什么条件下用正弦定理,什么条件下用余弦定理,什么条件下解三角形会产生两解;通过求三角形的边或角拓展问题,找出解三角形的一般方法;通过解题改编问题,找出处理三角形中角的关系式、边的关系式、三角函数关系式的一般规律.在操作中反思,学习质疑问题,培育理性精神;在求解中探索,激发学生的主体意识,拓展思维宽度;在解题后改编问题,发挥学生的主体作用,提炼思想方法.
(二)学情分析
学生对于正弦、余弦定理的简单应用是能够解决的.然而,他们对于“在什么条件下用正弦定理、什么条件下用余弦定理”存在疑虑,很少思考“为什么用正弦定理而不用余弦定理?”的问题,缺乏反思问题和质疑问题的意识,更想不到去拓展问题和改编问题.本节课的重点是:寻找求解三角形边和角的一般规律和方法;难点是:如何处理三角形中角的关系式、边的关系式以及三角函数关系式.
(三)教学过程
1.练习回顾


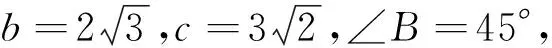
设置意图:给学生提供最简单、最直观的例子,让学生在操作中感悟问题及问题的解法.
2.提出问题
问题1 解完上述题目,你有什么感受?
活动预设:(1)解上述题目,需要用到哪些知识?
(2)在什么条件下用正弦定理,什么条件下用余弦定理?说明理由.
(3)题1能否用余弦定理来解?题2能否用正弦定理来解?题3呢?哪种方法更简单?说明理由.
(4)为什么题1和题2只有一个解而题3会产生两解?
设置意图:通过学生的解题,让学生谈感受.他们可以回顾所学知识,也可以对我们一般的解题方式提出质疑,也可以对上述三个问题进行比较等等.留出更多的时间,让学生说出自己的困惑,解答内心的疑虑.
例1 判定下列三角形各有几解?
(1)b=13,a=26,B=30°;
(2)c=16,b=26,C=30°;
(3)a=30,b=26,A=30°.
【回顾】判定三角形有几个解,关键是什么?
设置意图:由于本节课是习题课,学生已经学习了已知两边一对角判定其解的个数,这里一方面让学生复习巩固,另一方面把原来用式子表达:当bsinA 问题2 对于题2你认为还可以求什么? 活动预设:(1)求cosB、tanC;(2)求面积SΔABC;(3)求BC边上的高和中线以及∠B的平分线. 设置意图:把一个简单问题利用学生的聪明才智可以扩展出许多问题,给学生提供一个联想和发现的机会,演绎问题的变化过程,激发学生的主体意识. 图1 例2 如图1,在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BAD=60°,∠BCD=135°,求BC的长及sin∠ABC. 【回顾】在上述问题中,求三角形的边和角有怎样的规律? 设置意图:结合问题2中求BC边上的高和中线以及∠B的平分线,归纳并概括求解三角形边和角的一般思维方法,培养学生分析问题和解决问题的能力. 问题3 你能把题1做一些改变吗?变得更简单些或变得更难些. (2)△ABC中,A=4C,b=c,则∠C= ; 设置意图:依托题1进行的问题改编,有一定的开放空间.从边的数值和角的数值,上升到角与角的关系和边与边的关系,还可以利用三角函数的关系以及三角形面积、外接圆等,有些问题容易解,有些问题解起来有困难,可以留在课后.这里只是给学生搭建一个发挥想象、展示个性的创新平台,让学生的主体作用得到充分地发挥. 【回顾】①解上述问题有何规律? 设置意图:在开放的空间中聚焦到某一个问题上.总结处理角的关系和边的关系以及三角函数关系式的一般方法,提炼体现这些方法的数学思想. 3.课堂小结 (1)从知识角度看:正弦定理、余弦定理; (2)从思想方法角度讲:通过正、余弦定理来处理三角形中的角的关系式、边的关系式、三角函数的关系式,充分体现化归的思想方法; (3)在研究问题上,解题后学会反思问题,学会拓展问题,学会变更问题,从而提高课堂的效率和解题的价值. 习题课是数学教学的一类重要课型,怎样才能上好数学习题课?从解题的角度讲,我们希望用几个简单而典型的题目来解决较多的问题,更愿意看到学生经历一个由被动参与到主动探索的过程,培养学生思维能力.如何达成这些目标?以下从“三度”的角度来表述. 1.反思问题,增加知识的厚度 学生仅会解题,而题目是解不完的.因此我们增加了问题反思这样的教学环节,可以寻求一类问题的规律,更重要的是让学生从直观、感性逐步走向理性.首先,对知识和方法的反思.学生知道已知两角一边用正弦定理,已知三边用余弦定理,然而他们心中还是存有疑虑,为什么要这样呢?我们通过列方程或方程组回答了这个问题,在解除学生疑虑的同时体现了列方程的思想方法.其次,在解三角形中对解的个数的质疑.通过定量分析,由正弦定理、余弦定理的计算可知;再通过定性分析,由初中的三角形全等判定定理知,边边角无法判定两个三角形全等,说明已知两边一对角无法确定这个三角形,既增加了知识的可信度又增加了知识的厚度.最后,既然已知两边一对角无法确定这个三角形,那么它的解的情况会怎样?这是必然要回答的问题.所以在学生原有知识的基础上,对已知两边一对角有两解的条件进行了语言概括,让所学知识有一个螺旋上升的过程.这样的经验积累,既有学习方法上的积累又有知识的理解,更有利于学生对知识的灵活运用. 2.拓展问题,扩大思维的宽度 解题不是目的,是认识问题、扩展问题的开始.通过解答简单的题2,开始寻找可以求解的其它问题,将问题逐步向前推进,这样的探求过程演绎了问题的来龙去脉,以及各种不同的发展走向,问题由简单逐渐变为复杂,知识的运用也越来越灵活,开阔了学生的视野,打开了学生的思路.其次,如果说让学生反思可以缺少一点主动的话,那么拓展问题需要学生积极思考和主动参与,在相互交流和碰撞中,激发学生的主体意识,展示学生的聪明才智,让学生发现更多的问题,解决更多的问题,这样的一题多问是用学生的发现替代教师的提问,最大限度地扩展学生的思维,让学生从被动的解题者变为主动的出题人.最后,我们不能为了变化而变化,而要回归到某一个问题上来,在解决例2的过程中概括一般规律,总结思想方法,让学生真正体会到:“万变不离其宗”的道理. 3.改编问题,延伸课堂教学的长度 数学习题课关键在于调动学生的学习积极性,让学生由被动跟随转变为主动参与,再由主动参与变化为自主探索,这种探索不仅限于课内,还能延伸到课外,没有学生的兴趣和热爱是做不到的.只有这样才能增加知识的厚度,拓展思维的宽度并延伸课堂教学的长度.




二、教学感悟