零售商引入3PL服务商的分销供应链博弈与优化

（武汉理工大学 交通学院，湖北 武汉 430063）

1 引言

物流的发展一直备受国内外专家和学者的关注，管理学大师彼得德拉克将其称为“经济领域的黑暗大陆”，后来又被日本学者称为“第三方利润源泉”，足以说明人们对物流的重视，因此3PL服务商成为了人们研究的热点。

3PL服务商的业务广泛，在合作中极具灵活性，物流成本在产品价格中往往占比较大。白燕华等[1]通过分析标准和核心服务两种情况，参与者进行合作和不进行合作的供需关系，得出合作方互相信任的情况下合作可以实现共赢。韩超群[2]从VMI实施中存在的不足出发，分析引入3PL的供应链特点，找出VMI&TPL供应链能够形成的原因。郑长征等[3]研究了具有多个零售商的供应链，产品市场需求确定时，分析未和物流企业合作时的库存模型，解出了供应链参与者的最终策略。

虽然物流的发展呈现了大好的趋势，但物流企业与其他企业在实际合作中出现了很多不足。物流企业自身的技术和设备不完善，企业之间不信任，缺乏信息共享。因此，在合作过程中企业都会有所保留。杨怀珍等[4]在产品的需求不确定时，建立了供应链上游企业的增量利润分配模型：基于不对称Nash谈判的风险共担收益共享契约。魏杰等[5]利用博弈相关知识和模糊理论研究一个物流企业进行回收物流工作的环形供应链，建立了集中决策和分散决策下的博弈模型，得出了各成员的最优价格函数和最优回收系数。

2 模型建立

考虑单供应商和单零售商的分销供应链，零售商与3PL服务商合作，成本参数假设如下：设最终产品的市场需求量为Q，最终产品的单价为P，Q和P之间呈线性关系，Q=a-bP(a＞0,b＞0)。3PL服务商的单位运营成本为Cl，3PL服务商的单位服务价格为Pl，供应商的单位生产成本为Cs，供应商的单位库存持有成本为Hs，供应商的单位销售价格为Ps，设零售商的单位库存持有成本为Hr，设Wl、Ws、Wr、W分别为3PL服务商、供应商和零售商的利润函数及其总利润。此时，假设三者相互之间了解对方的成本水平，则可得：

3 模型求解

在独立决策下，第一阶段3PL服务商和制造商分别向零售商制定单位产品的服务价格，第二阶段由零售商决定终端产品的价格。决策过程均以决策者的利益最大化为目的。用“*”表示博弈均衡，采用动态博弈求解的逆向归纳法求解如下：

将Pl代回第二阶段可解得：

将Pl和Ps代回第一阶段可解得：

此时可求得：

在该分销供应链中，3PL服务商和供应商具有相同的最终利润，且这个利润是零售商利润的两倍。同样，所有利润函数随(Hr+Hs+Cs+Cl)变化而呈反方向变化。

4 模型优化

4.1 基于分散决策的收益共享机制

当3PL服务商与零售商合作时，将二者看作利益整体进行决策。在分散决策的条件下对系统进行优化，首先供应链成员在序贯博弈下依次独立决策，然后按照一定的分配比例分配系统的增量利润。

在独立决策下，第一阶段：3PL服务商和供应商作为一个利益整体，考虑整体的成本，以系统利润最大化为目标，确定总的服务价格。第二阶段：由零售商以自身利益最大化为目标，选择商品的终端产品价格。

假设三者基于讨价还价的分配比例已确定，设ρl、ρs、ρr分别为3PL服务商、供应商和零售商的利润分配比例，0≤ρl、ρs、ρr≤1 ，且ρl+ρs+ρr=1 。Wls为3PL服务商和供应商的总体利润函数，Pls为3PL服务商和零售商总服务价格。因此可得3PL服务商和供应商的目标函数为：

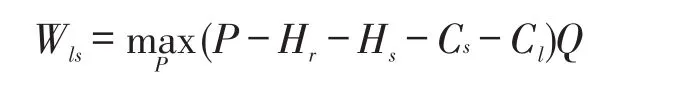
零售商的利润函数为：Wr=(P-Pls-Hr)Q

上标“s”表示博弈均衡，采用动态博弈求解的逆向归纳法求解，结果如下：

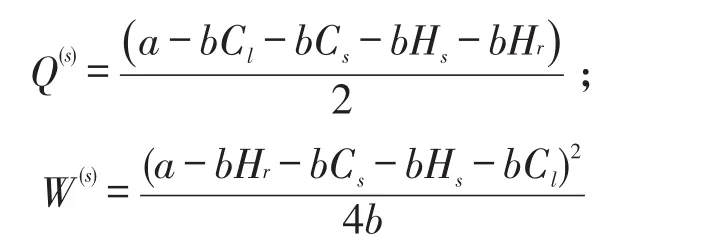
可推得系统的增量利润为：

3PL服务商的利润为：

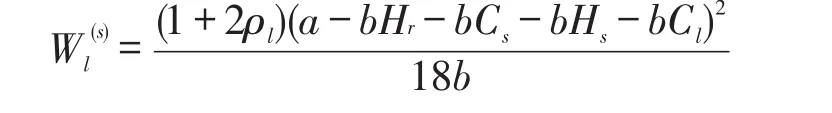
供应商的利润为：

零售商的利润为：

由结果可得：P*＞P(s)，Q*＜Q(s)，W*＜W(s)，该模型使市场价格降低，而市场需求的增加最终使得系统的总利润增加。为了使系统达到最优，3PL服务商和供应商作为整体时会选择自身的变动成本作为服务价格，3PL服务商、供应商和零售商的收益均因此增大。

4.2 基于合作决策的收益共享机制

在分销供应链中，为了获取更多的利润，企业之间往往会进行合作和收益共享。根据合作方的不同可以分为以下情形：情形1，3PL服务商与供应商进行合作和收益共享；情形2，3PL服务商与零售商进行合作和收益共享；情形3，供应商与零售商进行合作和收益共享；情形4，3PL服务商、供应商和零售商三方进行合作即集中决策和收益共享。合作的企业作为一个整体进行决策，并以自身的利益最大化为目标。

对情形1分析，3PL服务商与供应商签订合同，合作定价，在参与者依次决策后，3PL服务商与供应商对合作整体的总增量利润进行分配，设3PL服务商与供应商合作制定的价格为Pls，利润函数为Wls，3PL服务商与供应商的利润分配比例为，因此可得：

假设参与者了解彼此的成本水平，该博弈过程分为两个阶段，第一阶段：3PL服务商与供应商合作，一起向零售商制定单位服务价格；第二阶段：零售商决定终端产品的价格，采用动态博弈求解的逆向归纳法求解结果如下：

3PL服务商与供应商整体的利润为：

3PL服务商的利润为：

供应商的利润为：

对于情形2分析，3PL服务商与零售商合作，合作定价，在参与者依次决策后，合作双方对合作整体的总增量利润进行分配，设合作制定的价格为Plr，合作总体的利润函数为Wlr，3PL服务商与零售商的利润分配比例分别为，此时可得利润函数如下：

假设参与者了解彼此的成本水平，该博弈过程分为两个阶段，第一阶段：供应商选择服务价格；第二阶段：3PL服务商和零售商合作，选择终端产品的价格，采用动态博弈求解的逆向归纳法求解结果如下：

此时3PL服务商和零售商整体的利润为

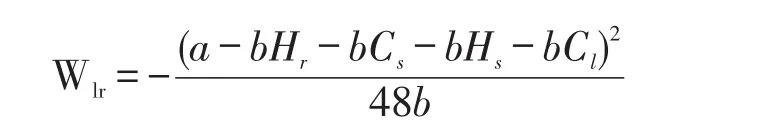
3PL服务商的利润为：

零售商的利润为：

因此，3PL服务商与零售商合作时：P*＞P(s)，，即3PL服务商与零售商合作降低了市场价格，增大市场的需求和系统利润。但是3PL服务商与零售商利润却有所降低，供应商的利润大幅增加。这表明3PL服务商与零售商合作，并不能达到增益的目的，除非与供应商一起进行系统的收益共享。

对于情形3分析，供应商与零售商进行合作定价。在参与者依次决策后，合作双方对合作整体的总增量利润进行分配。设合作制定的价格为Psr，合作的利润函数为Wsr，供应商与零售商利润分配比例分别为。此时可得利润函数如下：

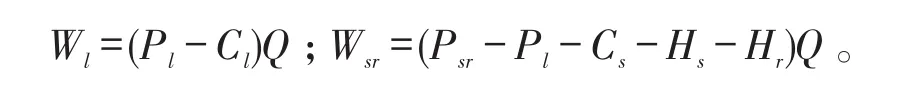
假设参与者了解彼此的成本水平。该博弈过程分为两个阶段：第一阶段：3PL服务商选择服务价格。第二阶段：供应商和零售商合作，选择终端产品的价格。采用动态博弈求解的逆向归纳法求解结果如下：

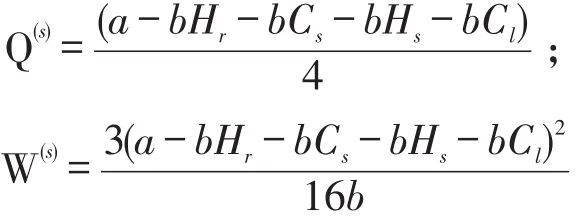
供应商和零售商整体的利润为：

3PL服务商的利润为：

供应商的利润为：

零售商的利润为：

因此，供应商与零售商合作时：P*＞P(s)，，因此，供应商与零售商合作也降低了市场价格，增大市场的需求和系统利润。但降低了供应商与零售商的总利润，零售商的利润大幅增加。所以，若没有零售商愿意进行系统的收益共享，供应商与零售商往往不会选择合作。

对情形4分析：在集中决策下对该供应链进行优化，各企业按照一定比例分配增量利润，分配比例由参与者讨价还价的能力确定。各企业要相互配合，进行信息共享。设3PL服务商、供应商和零售商的利润分配比例分别为：，且 ，，利润函数为Wlsr。

在集中决策下，零售商的目标函数为：

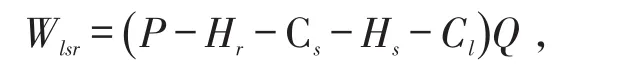
Wr取得最大值时，

则系统的利润为：

3PL服务商的利润为：

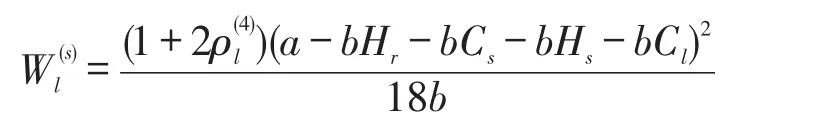
供应商的利润为：

零售商的利润为：

5 算例分析

表1 零售商引入3PL服务商时的博弈均衡结果

从表1可以看出，分散决策下的收益共享机制以自身成本作为服务价格，其市场价格和市场需求与集中决策下的相同，具有相同的增量利润和最大的系统利润；两方合作的收益共享机制，三种情况具有相同的市场价格和市场需求，且未参与合作的企业都获得了可观的收益。但只有在情形1中参与者的利润均增加，情形2和情形3中进行合作企业的利润都有一定的减少。

6 小结

当3PL服务商与零售商合作时，3PL服务商与供应商同为博弈先动者，在供应链中处于相同地位，因此获得的利润较零售商高，且3PL服务商与供应商获得的利润相等。分散决策下的收益共享机制与集中决策下的收益共享机制对供应链的优化效果相同，均使市场需求变为原来的4倍，弥补了市场价格降低的利润损失，供应链获得了相同的增量利润。而两方合作下的优化对系统整体优化的效果相同，市场需求变为原来的1.5倍，同样弥补了市场价格降低的利润损失，但系统增量利润较低，且对于每个参与者来说，并不一定得到优化。只有3PL服务商与供应商合作可以使合作方和非合作方的利润均增加。因此，总体来说，对系统进行优化都是通过降低市场价格和增加市场需求来实现的，而且基于三方的收益共享机制优于基于两方的收益共享机制，而分散决策下的收益共享机制优于集中决策下的收益共享机制。