复杂网络可视图及其在内河港口吞吐量预测中的应用

（浙江工商大学 管理工程与电子商务学院，浙江 杭州 310018）

1 引言

内河航运是我国交通运输体系中不可替代的重要组成部分，也是适应可持续发展的环境友好运输方式。内河航运与其他运输方式相比具有运输能力强、能源消耗低、低碳环保等特点。港口是内河航运最重要的部分，关系到内河航运的通行效率和安全性，港口系统的运行状况直接关系到内河航运的发展水平。

港口吞吐量是衡量内河港口发展规模和生产经营成果的重要指标之一，影响港口吞吐量的因素很多，如水文环境、港口建设水平、当地经济发展水平等。基于港口吞吐量时间序列具有随机性和非线性的特点，对其分析研究的方法主要有数理统计[1]、随机过程[2]和机器学习[3-4]等方法。近年来，为更为直观的反映时间序列特性，复杂网络被普遍用于各领域的时间序列研究，且取得了较为丰富的成果[5-7]。

2 可视图原理

复杂网络是研究时间序列的重要工具，可视图理论是从复杂网络视角对时间序列变化规律进行研究。近年来，可视图理论作为一种新兴的构建复杂网络的工具，已逐步形成一种算法体系。可视图理论具有连通性、无向性、稳定性等特点。连通性是指由于数据必然和其相邻时刻的数据可视，因此可视图网络必然连通，而不存在孤立点。无向性是指两点之间的“可视”是双向的，因此网络的边不考虑方向性。稳定性是指对数据进行横、纵坐标的重标度时，相应的网络结构保持不变。

为了更为直观地表达港口吞吐量时间序列的规律特征，采用可视图理论将港口吞吐量时间序列转化为复杂网络[8]。可视图算法主要包括两种：自然可视图算法和水平可视图算法。而时间序列的水平可视图只是自然可视图的一种特例。为更全面准确的体现数据间的关系，本文采用自然可视图算法对港口吞吐量时间序列进行研究。

我们用湖州港2012年12月吞吐量数据说明这一原理，12月份吞吐量柱状图如图1所示。若任意两柱顶点间无其他柱遮挡，则将其顶点直线相连。显然两个顶点间是相互可视的，从而所得网络为无向网络[9]。

从图1可明显看出24号和25号实际值比较大，但被实际值更大的23号和26号阻挡，从而度值偏小；而11号和15号实际值并不突出，但其度值相对较高；极少出现实际值很小而度值很大的情况。由此可见，在自然可视图中出现度值异常说明近期数据发生突变。

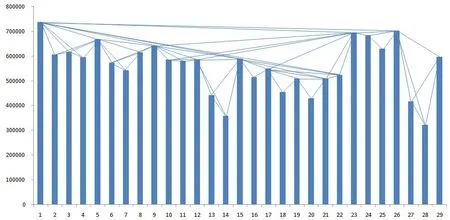
图1 12月份吞吐量数据柱状图

根据上述原理，可得到节点关系的连接矩阵，从而将吞吐量时间序列转化为复杂网络，如图2所示。

图2 12月份自然可视图

3 港口吞吐量可视图分析

为了直观地分析港口吞吐量时间序列的特征，实验数据源采用湖州港2012年总体及五个分港区（长兴、南浔、吴兴、安吉和德清）吞吐量时间序列。将六个时间序列按上述原理转化为自然可视图，如图3所示。

3.1 度分布分析

度分布能够较好地反映复杂网络的拓扑结构。由自然可视图原理可知，度值为1的节点极少且均出现在时间序列初始。为较准确地拟合函数，故将度值为1的节点删除，从而得到六个时间序列在双对数坐标下的拟合情况，如图4所示。六个网络度分布的幂指数比较见表1[10]。

由图4可知，六个吞吐量网络中度值较小的点概率比较大，且度分布具有较为明显的沿直线重尾分布。由表1可知，时间序列标准差和最大度值均与度分布幂指数呈反向相关关系。该现象表明港口吞吐量时间序列波动情况与其对应的自然可视图最大度值关系较为密切。

图3 各分港区吞吐量自然可视图

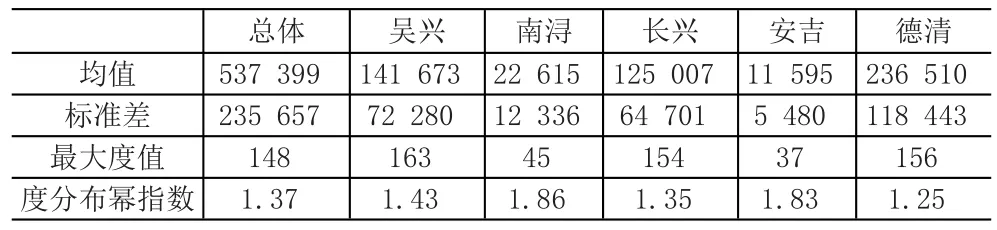
表1 可视图网络度分布指数比较

3.2 小世界效应分析

小世界特性是指网络具有较小的平均最短路径和较大聚类系数，可以对不同网络规模下聚类系数和平均最短路径变化的速度进行比较。

如果两节点之间由一系列首尾连接的边组合联接在一起，那么这个边组合便是两节点之间的一条路径。两节点之间边数最少的路径称之为最短路径，常记为dij，亦称为两节点之间的距离。任意两点间距离平均路径长度L：

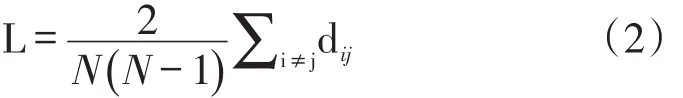
若时间节点i的度为ki，则其具有ki个邻居节点，聚类系数Di：

其中，Ci为该节点邻居节点实际连边数为最大连边数。

如果平均最短路径随着网络规模的增大呈现对数级的增长，即如果平均路径长度满足L(N)～lnN，同时聚类系数较大，在此情况下认为网络呈现出小世界特征。

港口吞吐量时间序列自然可视图的平均路径长度L(N)如图5所示。显然，随着节点数N的逐步增大，L(N)的增速趋于平缓。曲线拟合说明L(N)与N之间满足对数关系，由此可知港口吞吐量时间序列转化而成的自然可视图具有小世界特性。

3.3 等级结构分析

模块思想是网络等级结构的基础，复杂网络结构是指由诸多相互联系的模块按照一定规律组成。其特点是节点间的聚类系数较高，同时模块间的边连接较少。

港口吞吐量自然可视图网络聚类系数与度值关系如图6所示。可知度值较小的节点与hub节点基本处在同一直线，但图中仍有部分节点出现较为明显的偏移。为此将时间节点的单位由“天”改为“周”，得出相应的关系图如图7。研究结果表明，除南浔分港外，其余的港口吞吐量时间序列以周为单位其自然可视图等级结构十分明显，且指数均小于1。

3.4 分形分析

图4 自然可视图的度分布情况

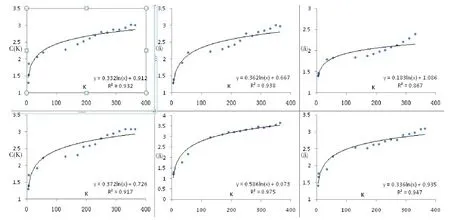
图5 自然可视图小世界特性

分形理论是在数学和分形维度的基础上描述和研究客观事实，可以更加符合的描述客观事实的复杂性和多样性。分形理论最重要的原则是自相似性原则，自相似原则指的是在系统中局部之间或局部与整体之间具有不同程度的相似性。基于网络图不考虑拓扑结构空间位置的特点，可知分形网络具有自相似性，但具有自相似原则的网络不一定分形。复杂网络分形特征和自相似特征可以通过经典的盒计数法进行判定。

图6 可视图网络等级结构特征（单位：日）

图7 可视图网络等级结构特征（单位：周）

盒计数法的基本思想是用不同边长的盒子不重叠的覆盖整个网络。显然每个盒子所覆盖的所有节点的距离都小于盒子尺寸LB，且当LB为1时需要盒子个数等于网络所有节点个数即网络尺寸，LB为网络尺寸时所需要盒子数为1。如果所需要的最少盒子数目NB与盒子尺寸LB之间的关系服从幂律分布，说明网络具有分形结构，即:

其中d为网络的分形维数。

利用盒计数法的贪婪着色算法对湖州港口吞吐量网络进行盒覆盖，不同盒子尺寸LB下所需的最少盒子数NB如图8所示。在双对数坐标中并未存在幂律分布的重尾现象，而是明显下凹形状。通过数据拟合也表明LB与NB呈指数分布，因此六个网络并非分形网络。通过网络重整化即新一次盒覆盖后，将盒子作为新的网络节点，由此发现重整化的新网络度分布仍呈幂律分布，但拟合度不断下降且度分布幂指数逐渐减小。结果表明六个网络并不存在自相似特征。

图8 可视图的分形分析

4 可视图分析对预测的作用

由前文分析可知，任意时间节点度值与任意数据点对之间的斜率存在一定的关系。因此在预测时间序列新时期数值之前，如能准确估算新时期节点的度值，就能计算新时期数值所处的区间。

为了说明可视图分析对预测的作用，本文选取吴兴分港区2012年每月吞吐量时间序列数据作为对象进行说明。首先将此时间序列数据通过可视图算法转换成复杂网络，如图9所示。

图9 吴兴港区月度吞吐量可视图

如预测吴兴港区第12月份吞吐量时，如能准确估算出第12月度值为2，显然第12月必然与第11月相连，同时与其他月份相连的个数有且只有一个。由于第11月仅与第10月相连（除第12月外，如图10所示），因此第12月与第10月必然存在边，故第12月预测值必然在第10月和第11月的斜率之上，即大于4 685 800。

此时第12月已与两个节点具有边关系，由于12月度值为2，故其不能再与第三个节点“可视”。结合图9和图10，第12月最有可能与第4月相连，故第12必然处于第4月与第10月的斜率之下，即第12月预测值必然小于5 160 870。因此第12月预测值必然处于区间[4 685 800，5 160 870]。第12月观测值为4 844 374显然满足条件。

由此看出，如能准确估算出预测的度值，便能很好地确定预测值所在的区间，且预测期的度值越大，预测区间更接近实际观测值。故而预测新周期数值问题可以转换成预测新周期的度值问题。

图10 吴兴港区前十一月吞吐量柱形图

5 结论

本文基于复杂网络可视图理论，对港口吞吐量时间序列进行研究。利用可视图理论将港口吞吐量时间序列转化为复杂网络，并对相应的网络特征进行分析。湖州港吞吐量时间序列可视图网络都呈现幂率分布，具有明显的小世界特性和等级网络结构。如能准确估算出新预测周期的度值，便能很好地确定预测值所在的区间，且新预测的周期度值越大，预测区间更精确。本文将预测港口吞吐量数值问题转换成预测港口吞吐量可视图网络的度值问题，为研究港口时间序列数据提供了一种新的思路。