条件矩约束下一阶自回归模型的参数经验似然推断

彭毳鑫，胡 敏，赵志文

（吉林师范大学a.大学外语部；b.数学学院，吉林 四平 136000）

0 引言

考虑如下的一阶自回归模型：

对于自回归模型的统计推断，一直是统计学家关心的热点问题之一。常学将和刘维奇[1]讨论了自回归模型的模型识别及其参数的高阶Yule-Walker估计；倪均援[2]讨论了有AR残差的自回归模型的参数估计和定阶问题；国春光等[3]提出一种求解扰动项序列自相关系数及估计自回归模型参数的迭代方法；林正华和冯仁忠[4]基于约束规划及计算数学理论，给出了自回归模型参数精确最小二乘估计方法；姜礼平[5]讨论了有噪声情形下自回归模型参数的估计问题以及模型定阶问题；吕效国等[6]研究了基于时间序列观测数据，如何选择自回归模型的必要条件；吴鑑洪和朱力行[7]给出了一些诊断检验工具，用于向量自回归模型的拟合优度检验问题；Chen等[8]利用非参数方法——经验似然方法估计自回归模型参数。本文进一步利用经验似然方法，讨论由辅助信息条件下模型（1）的参数估计问题。

经验似然方法是Owen[9，10]提出的一种非参数估计方法。经验似然方法有很多优点，如置信区域由数据本身决定，经验似然比统计量的极限分布为卡方分布，因此在构造未知参数的置信区域时无需进一步估计渐近方差等。经验似然方法最初主要用于总体均值的参数估计。近些年，该方法也被用于时间序列模型的统计推断问题，如Chan和Ling[11]讨论了GARCH模型的经验似然统计推断问题；Chen和Gao[12]讨论了时间序列回归模型的适应经验似然检验问题；Zhao和Wang[13，14]分别讨论了具有解释变量的自回归模型和随机系数自回归模型参数的经验似然统计推断问题，构造了未知参数的经验似然比统计量，同时证明了统计量的极限分布为卡方分布；Chen等[15]讨论了门限自回归模型的经验似然统计推断问题。

在实际中，基于样本观测数据 X0，X1，…，Xn，经常能够获得一些辅助信息，这些辅助信息的形式多种多样，如总体的分布为对称的或非负的，方差是均值的函数等等。如果在统计推断中有效的利用这些辅助信息，能够提高统计推断的精确性。本文中假定辅助信息能够表示成为如下的条件矩：

其中 t=1，2，…，β0∈Rd为未知参数，g(Xt，Xt-1;β0)∈Rr，且 r≥d 。 为了叙述方便，将 g(Xt，Xt-1;β0)简记为 gt(β0)。条件矩约束（2）包含广泛的辅助信息类，如果条件方差为某一已知常数，序列的二阶条件矩等于某一常数等。本文利用经验似然方法，给出模型（1）已知辅助信息（2）时，参数α的估计问题。

1 方法和主要结果

本文讨论如何应用经验似然方法估计模型（1）中的未知参数α。假定如下条件成立：

A1:|α|＜1，即模型为平稳遍历的；

A2: 存在 β0使得 E(gt(β0))=0;

下面讨论未知参数α的估计。

首先基于经验似然方法，获得数据驱动的权。具体地，基于辅助信息 E(gt(β0))=0，令：

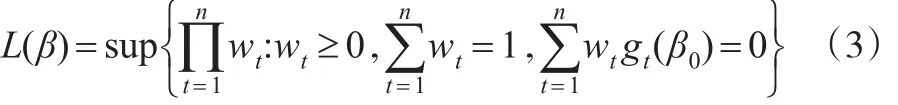
其中参数β0为待估的未知参数。由此可以获得使L(β)达到最大的权w1，w2，…wn。基于该权函数，用如下的加权最小二乘方法估计未知参数α，即：

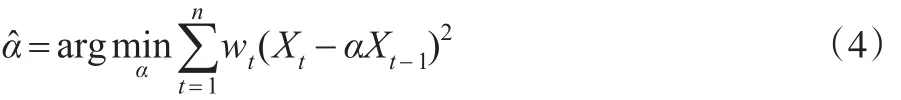
利用类似Owen[9]的方法，引入拉格朗日乘子λβ0∈Rr，经过简单的代数运算可知：

其中λβ0满足：

利用权（5），可以得到α的估计：

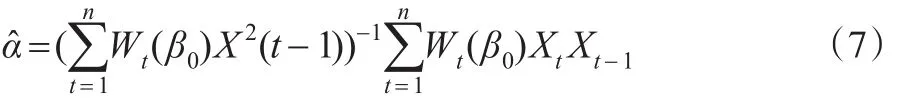
下面的定理给出了的极限分布。

定理1：假定条件A1-A2成立。如果α0是未知参数α的真值，那么：

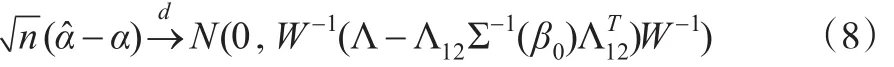
对于普通的最小二乘估计，其渐近方差为W-1ΛW-1。注意到Λ和Σ-1(β0)是正定的矩阵，因此与普通的最小二乘估计相比，本文所得到的估计的渐近方差减小。此结果进一步说明由于引入辅助信息，从而提高了估计的效。对于估计表达式（7），由于参数β0未知，因此，在实际中还无法使用该表达式估计未知参数α。为此，进一步使用最大经验似然估计方法估计未知参数β0。具体地，令，利用Qin 和Lawless[16]的方法，进一步可知：

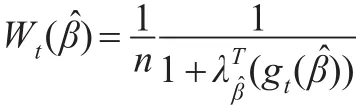
其中 (λβ，)满足：

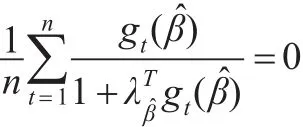
以及

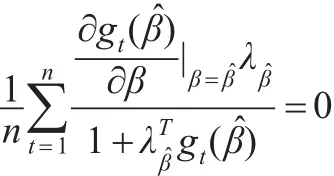
进一步令：

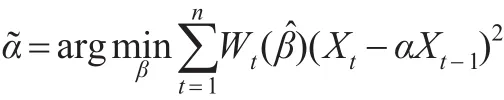
由此，可以用估计未知参数α。若r=d，即gt(β)的维数与β的维数相等，则，因此为普通的最小二乘估计。若r＞d，则加权最小二乘估计具有更小的渐近方差，因而与普通的最小二乘估计相比，加权最小二乘估计提高了估计的效。

下面的定理给出了估计量的极限性质。

定理2：若条件A1-A2成立，EX4t＜+∞，如果α0是未知参数α的真值，那么：

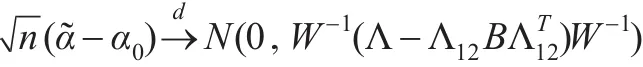
2 随机模拟

下面通过随机模拟来说明本文的方法的可行性。考虑如下的模型：

其中τ是固定的常数满足0，＜τ＜1，Φ(x)是标准正态分布N(0，1)的分布函数。

计算具有辅助信息下加权条件最小二乘估计的均方误差，即1000次估计误差平方的平均值。样本容量n=30， 50， 100。对于模型A，参数α分别取为-0.1，-0.2，-0.3，-0.4，-0.5，-0.6，-0.7，-0.8，-0.9，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，模拟结果由表1给出。对于模型B，参 数α分 别取为-0.1，-0.3，-0.5，-0.7，-0.9，0.1，0.3，0.5，0.7，0.9。τ分别取为0.8以及0.9表示不同的污染水平，模拟结果由表2给出。

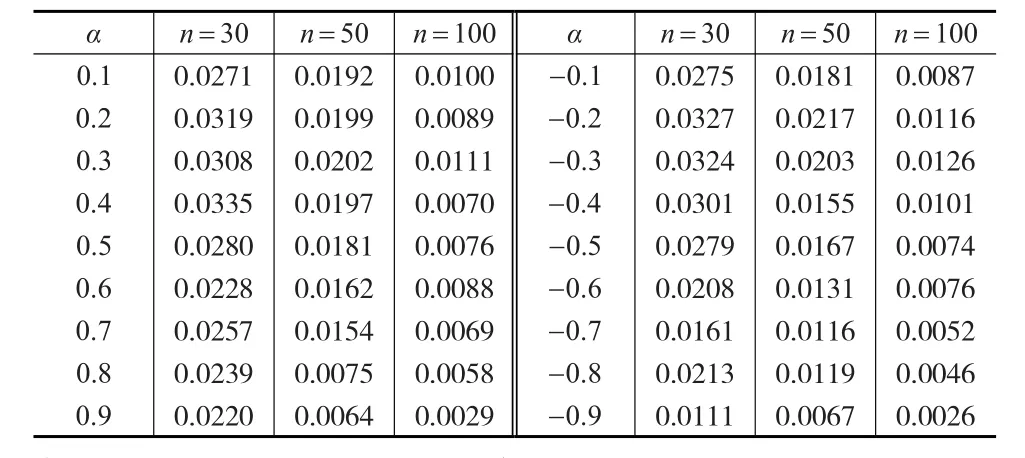
表1 模型A下参数估计的均方误差

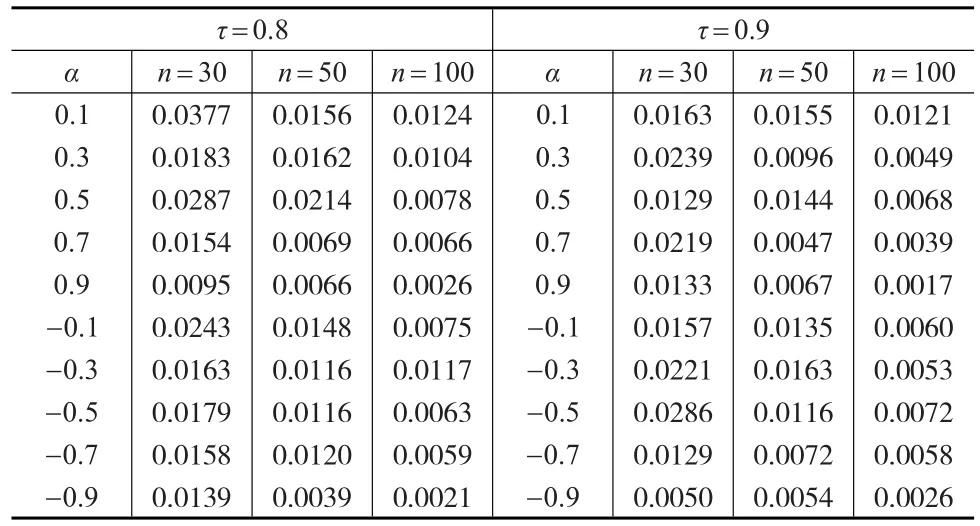
表2 模型B下参数估计的均方误差

从表1和表2的模拟结果可以看出，对于不同的参数以及不同的样本容量，本文的方法都具有较小的均方误差，这也说明方法具有稳健性。

3 定理的证明

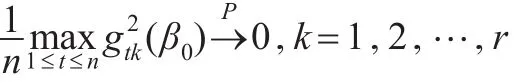
由条件A1可知：

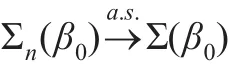
因此利用类似Peng等[17]引理1的方法证明，可以证明引理1成立。

引理2：假定A1-A2成立，EX41＜+∞，那么：

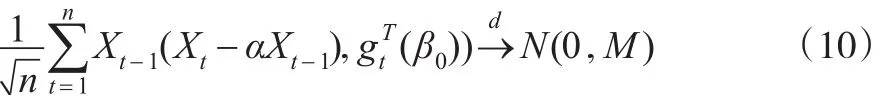
证明：由Cramer-Wold法则，只需证明对任意的非零向量C∈Rr+1，

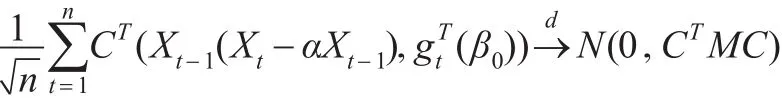
首先证明定理1，为此需要证明以下几个引理。

引理1：假定条件A1-A2成立，那么：，因此：

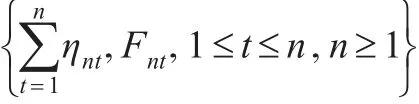
是零均值平方可积鞅阵，利用鞅的中心极限定理[18]只需证明：

以及

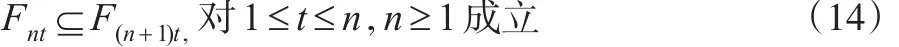
由σ代数的定义可知式（14）显然成立。下面证明式（11），注意到对∀ε＞0，

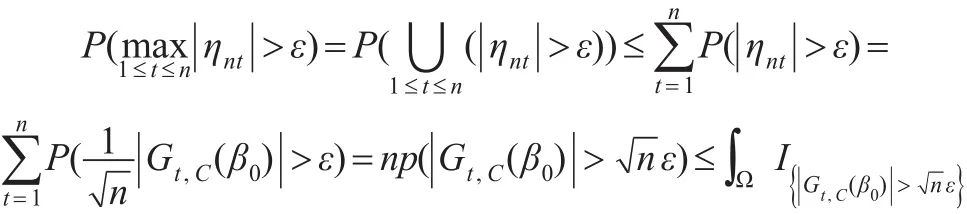
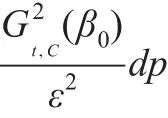
下面证明式（12）。由Lebesgue控制收敛定理可知：

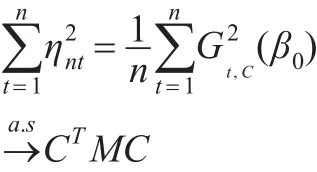
因此式（12）成立。

下面，证明（13）式。注意到：

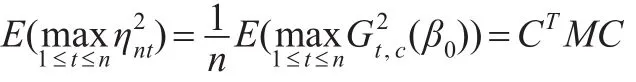
因此式（13）成立。综上可知引理2成立。

引理3：假定A1-A2成立，EX41＜+∞，那么：

使用类似Owen[9]中的证明方法可以证明式（15）成立。

定理1的证明

由式（6）可知：

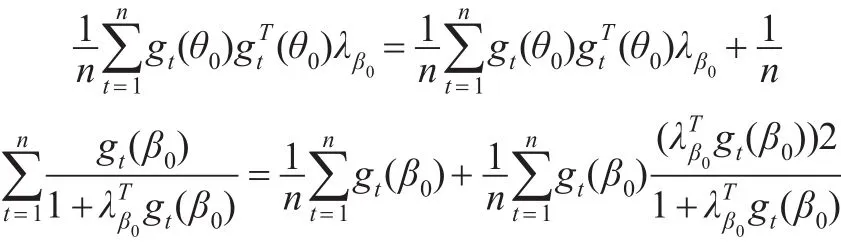
因此有：

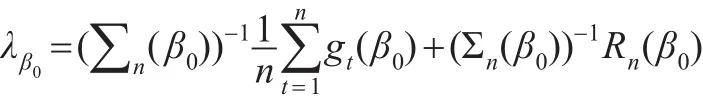
其中：

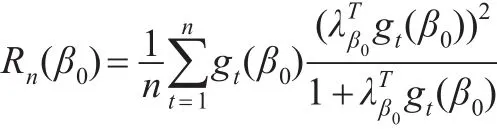
由引理1和2可知：

注意到对于∀t，

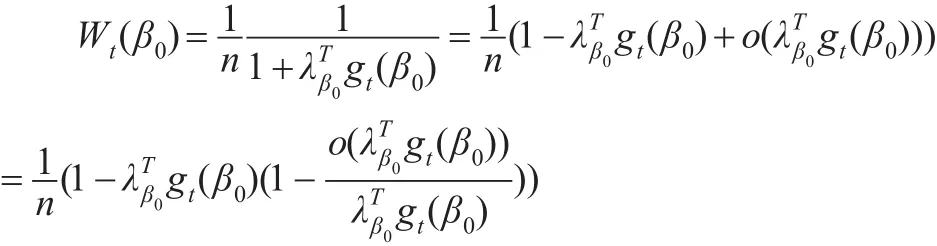
进一步由引理1和引理2可知：

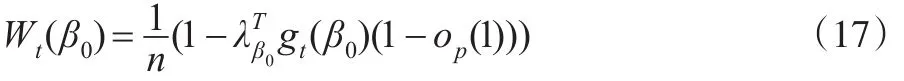
注意到：

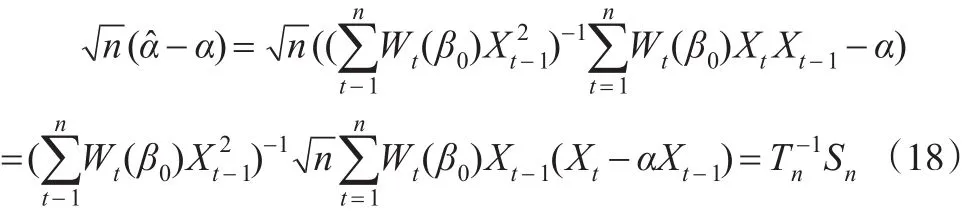
首先考虑Tn，由式（18）可知：

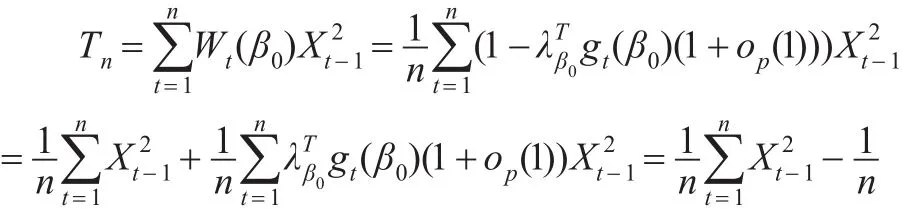
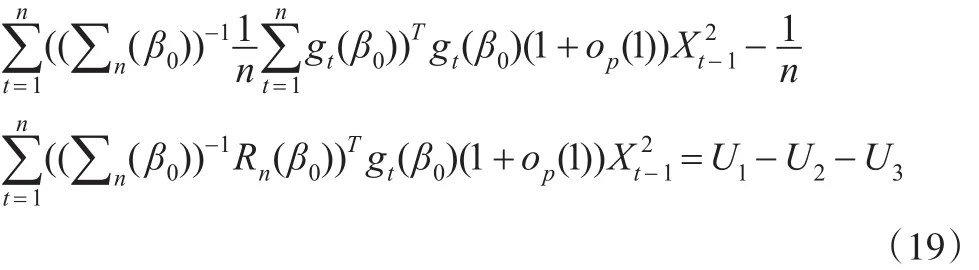
由条件A1和A2以及遍历性定理可知：

同理可知：

综合式（19）至式（21）可知：

下面考虑Sn，注意到：

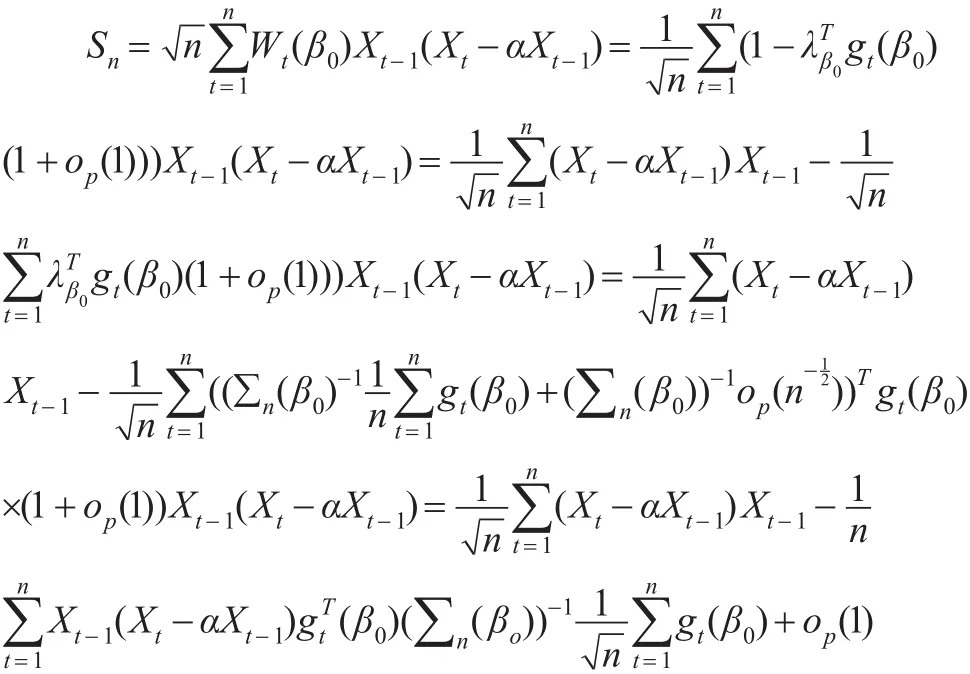
由遍历性定理可知：

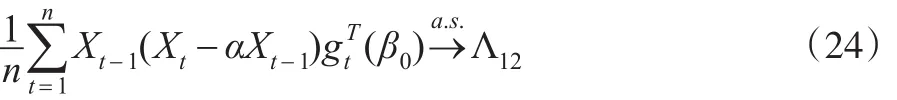
因此由式（10）以及式（24）可知：

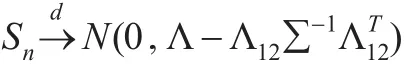
由此证明了定理1。

类似定理1的证明，可以证明定理2。

4 结论

本文主要利用非参数方法——经验似然方法讨论了当辅助信息可以用条件矩约束表示时一阶自回归模型参数的估计问题。该方法与没有利用辅助信息的模型参数的最小二乘估计相比较，具有更小的渐近方差。因此，有了更多的样有本信息，得到的估计具有更高的效果。