一道具有生活情景压轴题的原创过程*
●
(华东师范大学宁波艺术实验学校,浙江 宁波 315100)
一次中考数学命题时,笔者作为命题组组长,感到压力很大,尤其是压轴题的命制苦思冥想了许久.压轴题有很高的要求:一要知识综合;二要考查能力;三要梯度明显.
命题组首先要确定问题的背景,是函数、圆还是四边形?后来都被否定了,理由是想以生活实际问题作为背景,中考压轴题生活化是许多年来很少尝试的大胆创举,命题组想试一试.
1 问题的来源
笔者曾学过木工,做过圆形桌面,那时候买一张矩形木屑板,按如图1所示的方法锯两个半圆,拼成的圆桌面可以坐10个人.
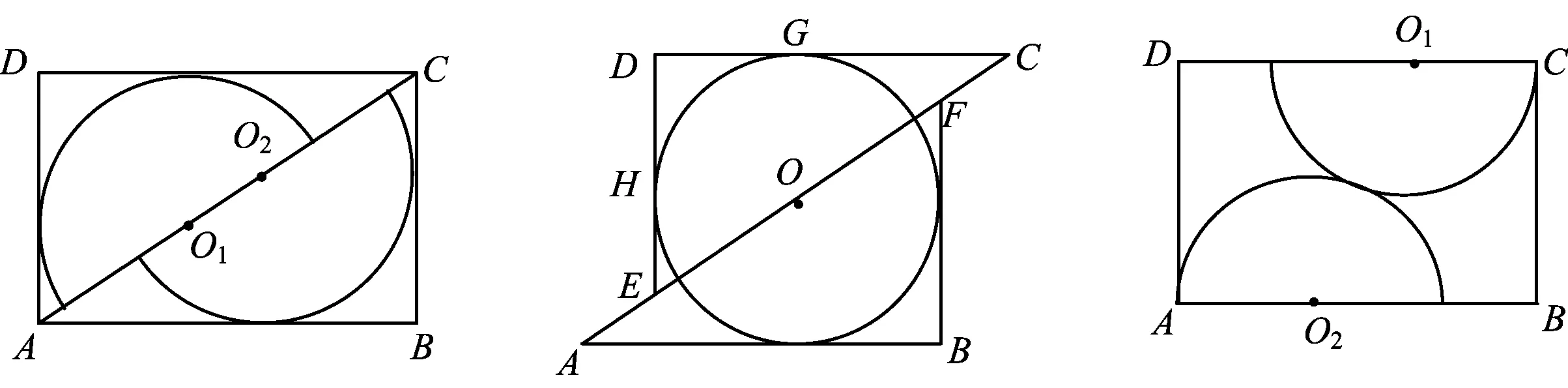
图1 图2 图3
实际操作是按图2划线的,即将木屑板沿对角线锯开,平移使其出现正方形,然后画出一个圆并锯下,这样操作要比图1画出2个半圆再锯下简单多了.
2 曾经的原题
在这个基础上,笔者曾编制过这样一道题:
问题1(原题) 已知矩形ABCD的边长AB=6,BC=4,请在其内画出两个最大的半圆,使这两个半圆可以拼成一个圆,求圆的半径.
最大半圆的位置如图1所示.有人质疑:如何证明这样画的圆的半径最大?如图3所示的画法也可以得到最大的半圆,还有其他情形吗?
3 初稿的设计
3.1 初稿的表述
为了回避以上这个难以回答的问题,命题组将原题改编成如下的命题:
问题2(初稿) 在矩形木板ABCD中,AB=3,BC=2,用这样的木板做一个尽可能大的圆形桌面,设计了以下两种方案:
方案1如图3,圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;
方案2如图2,沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆.
分别求两种方案圆的半径.
3.2 初稿的遗憾
这样的设计缺少新意,类似的问题以前已出现过.如何突破呢?如何让函数、方程融入其中呢?最好能考查学生的探索能力[1].笔者做圆桌面的经历再次浮现.
4 问题的探索
那时笔者按图2的方法做好圆桌面后,发现邻居家的圆桌面是如图4那样拼的,即一个大弓形与一个小弓形拼在一起.同样尺寸的一块木板,按图2或图4做圆桌面到底哪个半径大呢?这个问题让笔者纠结了很多年.
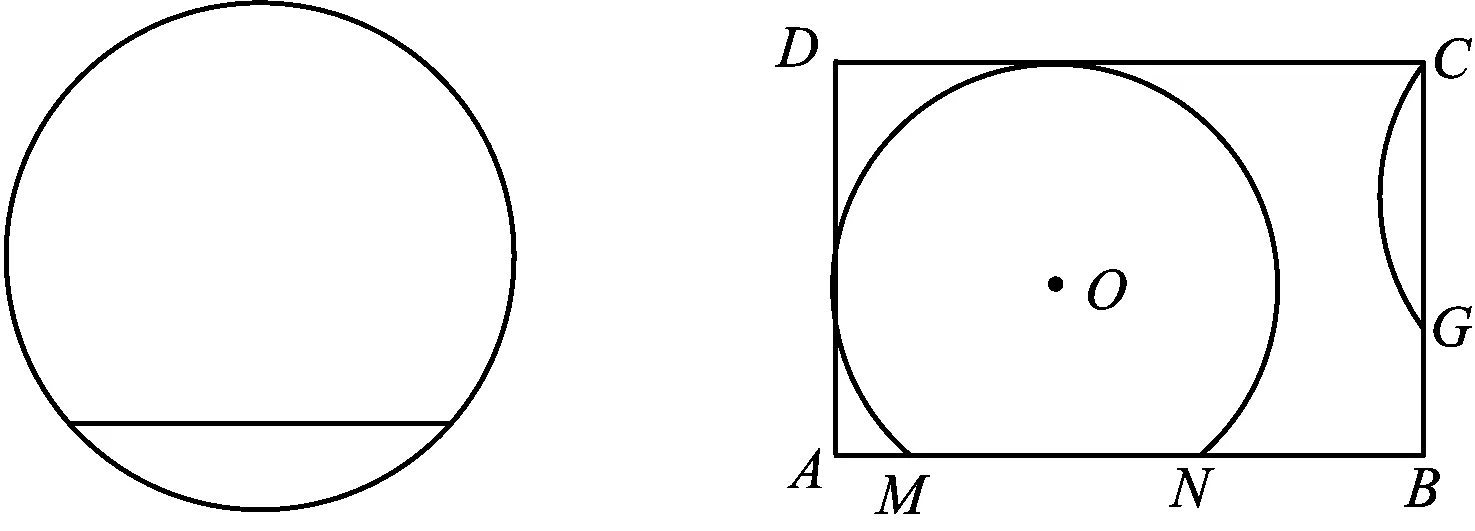
图4 图5
这次一定要研究个水落石出,笔者在纸上画出如图5所示的图形,在矩形内画一个比半圆大的弓形,分别与AD,DC相切,即圆心O在∠D的平分线上,弦MN在AB上;再在矩形剩余部分画一个比半圆小的弓形,弦CG在CB上,两个弓形正好能拼成一个圆.如何求这种拼接方法圆的最大半径呢?笔者决定借助几何画板来探索.
4.1 画图
打开几何画板,如图6,画一个矩形ABCD,使AB∶BC=3∶2(这个比例是笔者随便取的),按以下5个步骤画图:
1)作∠ADC的平分线,在其上取动点O;
2)作与AD,DC都相切的⊙O,交AB于点M,N;
3)作与AB垂直的⊙O的切线EF;
4)以MC为斜边作等腰Rt△MPC;
5)以点P为旋转中心,将矩形下方的弓形顺时针旋转90°得到以CG为弦的弓形.
这时惊奇地发现旋转后的点G一定在BC上,也就是说NP和GP垂直且相等,这个发现可以作为一个问题让学生探索,下面会再次涉及这个问题.
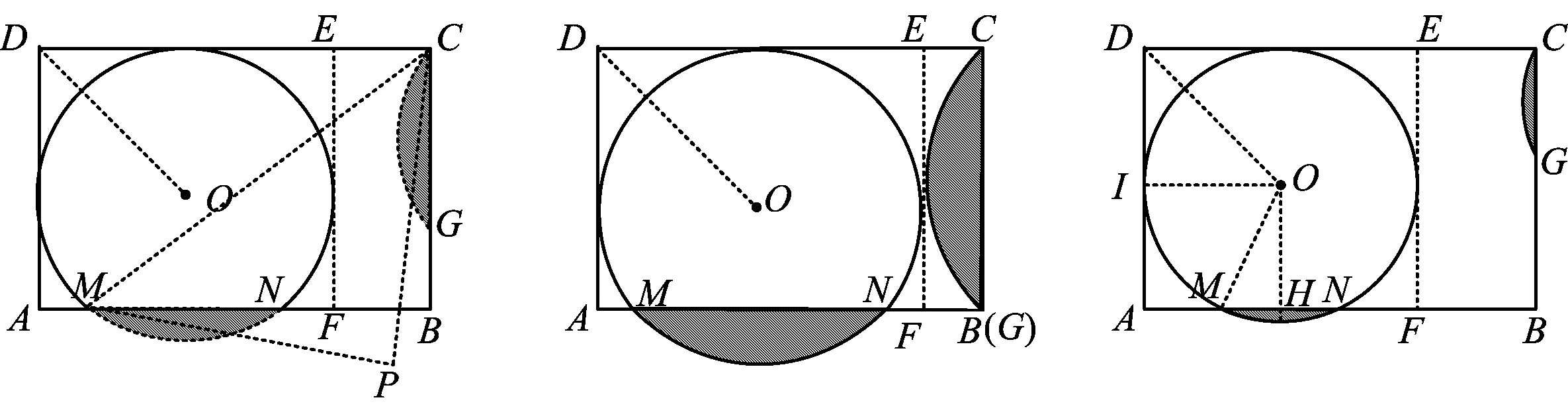
图6 图7 图8
4.2 计算
如图8,设AD=2,AB=3,设半径OI=OM=ID=x,则
当CG=BC=2时,⊙O的半径最大,此时
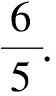
5 第二稿出台
5.1 第二稿表述
问题3(第二稿)
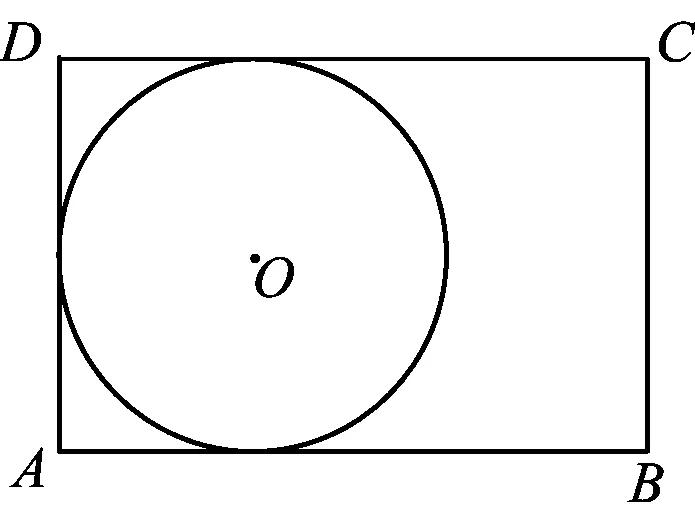
图9
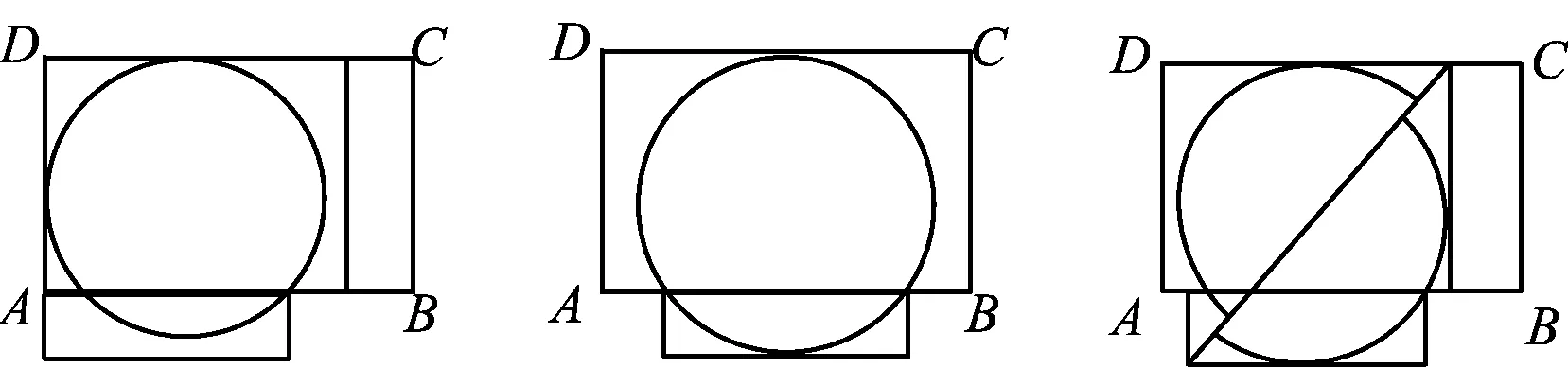
情景展现黄木匠用长AB=3、宽BC=2的矩形木板做一个圆桌面.他想如果直接锯下一个完整的圆,直径只有2(如图9);如果锯下两个半圆拼成一个圆,直径会大一些.于是他设计了两种方案:
方案1如图3,圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,画两个外切的半圆;
方案2如图1,沿对角线AC将矩形木板分成两个直角三角形,在每一个三角形内画出最大的半圆.
问题解决1)方案1中圆的半径长是______;方案2中圆的半径长是______.
深入探究黄木匠又想,如果锯下两个弓形拼成一个圆,情况又如何呢?于是他又设计了一个方案.
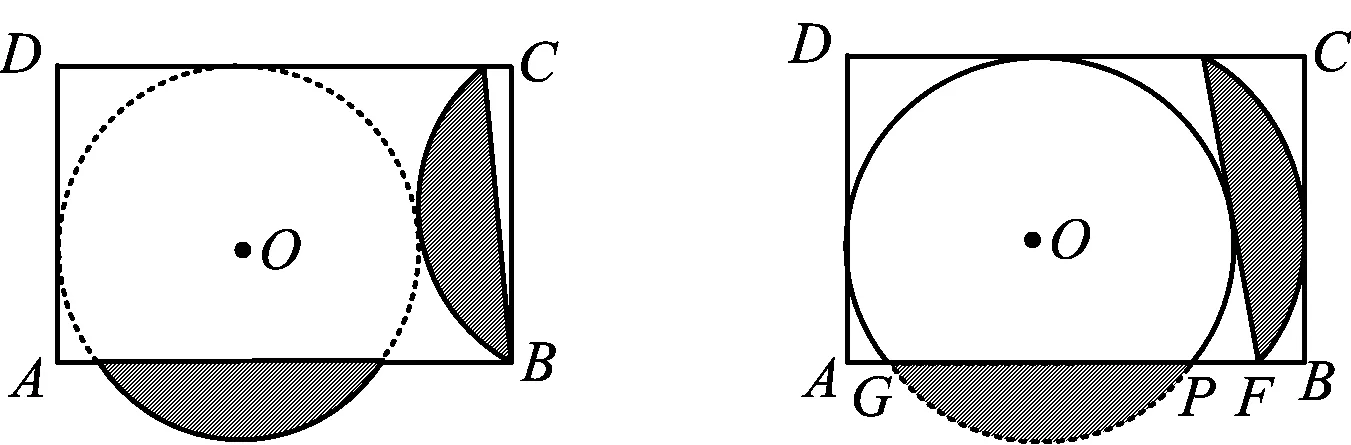
方案3如图5,画一个比半圆大的弓形(称为优弓形),分别与AD,DC相切,圆心为O,弦MN在AB上.再在矩形剩余部分画一个比半圆小的弓形(称为劣弓形),弦CG在CB上,优弓形和劣弓形正好能拼成一个圆.
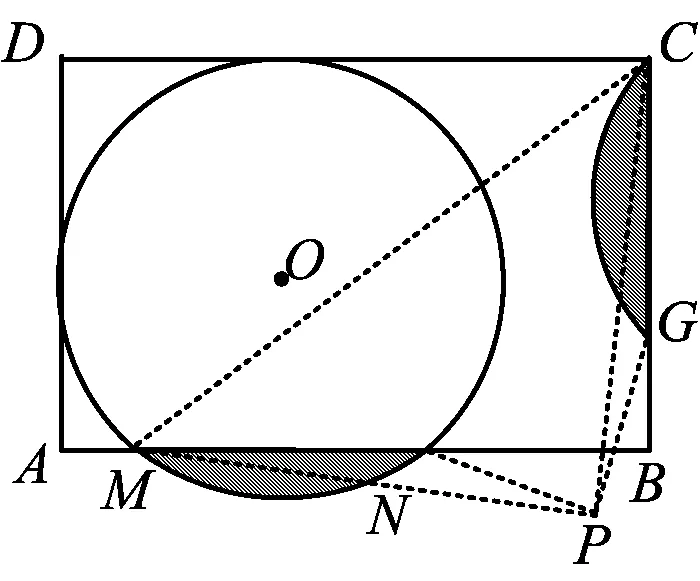
图10
如何画出劣弓形呢?如图10,以MC为斜边作等腰Rt△CPM,以点P为旋转中心,顺时针旋转90°,矩形外的劣弓形就被变换至矩形内了,这是为什么呢?问题归结为下面的证明.
2)求证:PN=PG,PN⊥PG.
最后结论3)设方案3中优弓形的半径为x,GB=y.
①写出y关于x的函数解析式;
②显然当y=0时圆的半径最大,那么3个方案中圆桌面半径哪个最大?
5.2 第二稿的遗憾
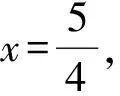
6 定稿的诞生
命题组要做的首先是对题目进行“减肥”,其次考虑把两个弓形拼一个圆的过程让学生来操作、探索[2].经过反复打磨、研讨和修改,定稿终于诞生.
6.1 定稿的表述
问题4(定稿) 木匠黄师傅用长AB=3、宽BC=2的矩形木板做一个尽可能大的圆形桌面.他设计了4种方案(如图11):
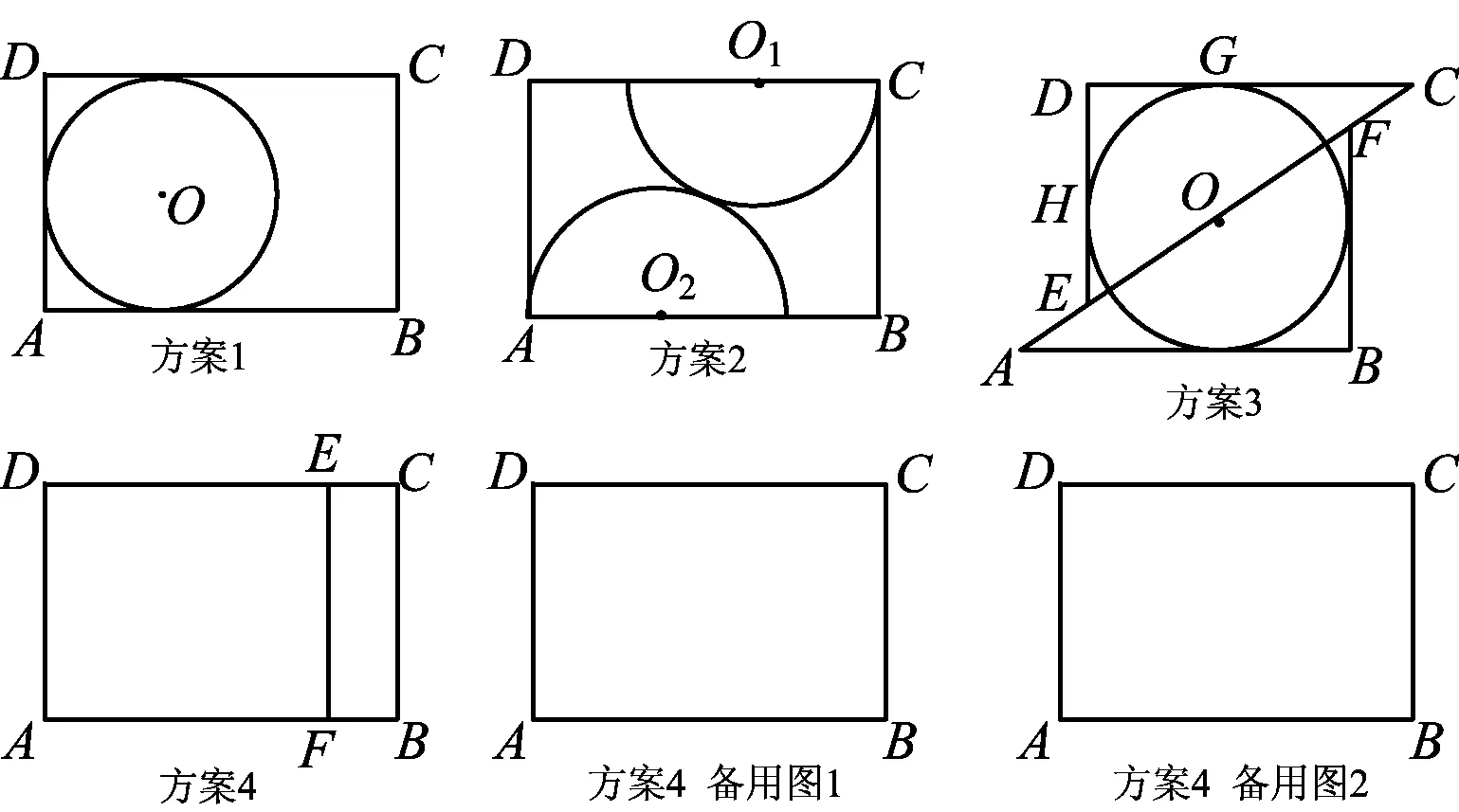
图11
方案1直接锯一个半径最大的圆.
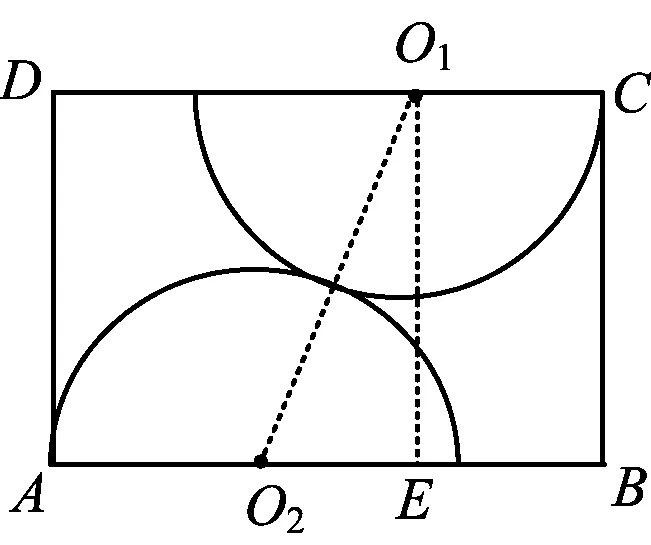
方案2圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆.
方案3沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆.
方案4锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.
1)写出方案1中圆的半径.
2)通过计算说明在方案2和方案3中,哪个圆的半径较大?
3)在方案4中,设CE=x(其中0 ①求y关于x的函数解析式; ②当x取何值时圆的半径最大,最大半径为多少?请说明4种方案中哪一个圆形桌面的半径最大. 最后的定稿所涉及到的核心知识有直线和圆、圆和圆、勾股定理、相似三角形、函数、方程.所涉及到的核心能力有直观想象能力、运算能力、推理能力和建模能力.学生通过操作、探究发现解决问题的方法,考查了学生的问题解决能力.此题起点低,综合性强,区分度好,中考结束受到师生、家长和媒体的一致好评. 第1)小题较为简单,学生容易上手;第2)小题考查的知识比较综合,难度有所上升;第3)小题第①问的函数要分类讨论,为第②问埋下伏笔,对学生的阅读理解能力、画图探究能力、分类讨论能力、运用多种数学思想和方法的能力提出了较高的要求. 《义务教育数学课程标准》指出:初步学会在具体的情境中从数学的角度发现问题和提出问题,并综合运用数学知识和方法等解决简单的实际问题,增强应用意识,提高实践能力.由此可见,将实实在在的生活问题作为数学题是符合课标理念的,值得提倡. 1),2)略. 图12 图13 图14 这说明圆恰好经过点P. 表1 中考压轴题的难度系数 从难度系数看,梯度比较合理.第3)小题的困难主要来自于如图12~14的方案设计,从而说明现在的初中学生解决问题的能力尤其是解决实际生活问题的能力有待提高. 图15 在方案2中,学生添出如图15的辅助线不难,但用圆的半径表示线段O2E发生了困难.在方案3中没有想到联结OG或OH,而是延长DE交AB于点M,结果计算陷入了困境. 在方案4中,学生不合理的做法有3种:其一是如图16那样的剪拼,结果圆的半径就小于如图14的半径;其二是如图17那样的剪拼,这是题意理解出错;其三是如图18那样的剪拼,这是受到方案2的影响,问题复杂化了,而且结果圆的半径依然小于如图14的半径. 图16 图17 图18 看来方案4的文字叙述指向还可以更加明确,避免学生用两个半圆拼接. 探索1矩形的长宽比. 若⊙O刚好经过矩形PMNG的一个顶点P,那么 OP2=OQ2+QP2=r2, 化简得 a∶b=3∶ 2. 综上所述,只有当a∶b=3∶ 2时,最大的⊙O恰好经过点P.运气真好,在几何画板中作图时,笔者随意取的长为3、宽为2的矩形,居然取对了. 探索2圆的半径还能大. 如图7,⊙O和劣弓形都与EF相切时,⊙O与劣弓形相离.在图7的基础上如果⊙O半径再增大,同时劣弓形端点C沿CD向左移动,使⊙O与劣弓形相切,如图19,圆的半径还要更大些. 图19 图20 在图19中⊙O的半径是多少?如果劣弓形画成如图20的位置,情况又如何呢?这些问题可以继续研究. 通过本次压轴题的命制过程,我们命题组有了以下体会、反思和成就感: 1)生活中有数学,数学可以为生活服务; 2)命制生活实际问题的数学题,要求教师关注生活,学会观察和思考,数学地看待生活问题[3]; 3)借助于几何画板命题,能提高对问题探索的有效性; 4)近年来各地中考以函数图像为背景的压轴题越来越少,取而代之的是有鲜活背景材料的新颖题,我们要继续努力寻找实实在在的生活材料; 5)定稿中的最后一个问题难度系数比较小,原因是学生难以设计“拼”和“画”的方案. 笔者反思:教学中应该重视培养学生的多种能力,包括动手操作和方案设计能力,让数学活起来.6.2 点评
6.3 解答
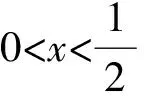

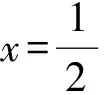
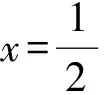
7 阅卷反馈
7.1 难度系数(见表1)

7.2 学生解答中的问题
8 问题再探索
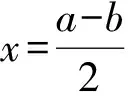
9 体会与反思

