考知识 重推理 注运算 显素养*——2018年浙江省数学高考试卷第19题阅卷有感

●

(杭州第七中学,浙江 杭州 310024)

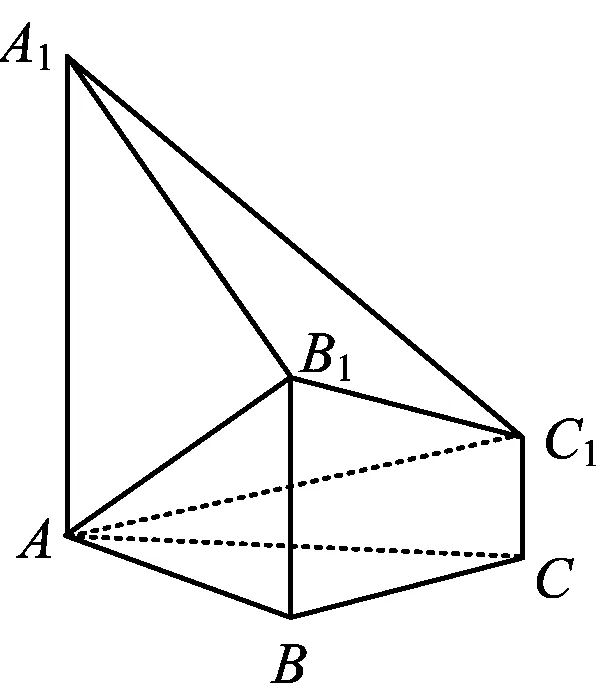
图1

1 原题赏析

题目如图1，已知多面体ABC-A1B1C1，AA1，BB1，CC1均垂直于平面ABC，∠ABC=120°，AA1=4，CC1=1，AB=BC=BB1=2.

1)证明：AB1⊥平面A1B1C1；

2)求直线AC1与平面ABB1所成角的正弦值.

(2018年浙江省数学高考试题第19题)

2 原题剖析

本题主要考查空间点、线、面之间位置关系以及直线与平面所成角等基础知识.同时，考查考生空间想象能力、逻辑推理能力和运算求解能力，综合体现了高中数学核心素养，具体特点如下：

1)覆盖广，重“四基”.本题是解答题的第二大题，属于偏简单的中档题，起点很低，入口很宽，大多数考生都可以解答.但是，考查内容非常丰富，包含立体几何中点、线、面之间的位置关系，比如线线垂直、线线平行、线面垂直、线面平行、面面垂直等判定定理和性质定理等，故试题设计上非常注重内容的覆盖面，注重考查学生在立体几何方面的基础知识、基本技能、基本思想、基本活动经验.

2)通法多，显“四能”.第2)小题考查空间角的内容，选择了解题方法最多的线面角，既体现了通法的丰富，也凸显了学生发现、提出问题的能力和分析、解决问题的能力.

由于每种通法都可以归结为原理选择的不同，从而对应逻辑推理能力、空间想象能力和运算能力的难度也不尽相同.若用几何法，则凸显空间想象能力；若用建立空间直角坐标系的代数法，则凸显运算能力.当然，有时需要两者兼具.

这说明试题命题者充分尊重学生个体差异，求同存异，体现公平性原则，也体现了高中数学核心素养的本质.

3)传承好，启来年.结合2017年浙江省数学高考试题第19题不难发现，本题仍然是求解线面角.不仅如此，其中利用线面平行方法(2017年给出的标准答案)解决点到面的距离，一目了然——秒杀.

同时，2017年这道试题除去0分后平均得分为9.08分，难度系数为0.56[1].2018年除去0分后平均得分为11分左右，难度系数为0.73.这说明经过这两年的改革，这道题的考查回归到了以往的文科题难度.

3 解法探析

当然，好的试题需要有好的评分标准，以实现命题者最初的命题意图.基于该试题的以上3个特点，本题阅卷组最终给出了各种版本的参考答案及其相应得分点，具体如下：

1)证法1由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得

从而

于是

AB1⊥A1B1.

由BC=2，BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得

由AB=BC=2,∠ABC=120°得

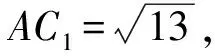
于是

AB1⊥B1C1,

因此AB1⊥平面A1B1C1.

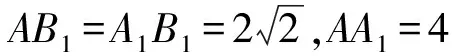
答题情况用几何法，先由勾股定理得到线线垂直，再用线面垂直判定定理得证.但在阅卷过程中发现：不少考生在利用勾股定理的时候，边长计算错误率较高，导致过程分被扣；还有部分考生算不出边长的结果，就试卷留白，这不可取，因为只要写出判断依据就可以得2分；还有部分考生因知识点错误，只证明了一个线线垂直就得到线面垂直被扣4分.而这个原因的产生，主要是在学习线面垂直时，没有很好地理解线面垂直判定定理.由于《数学(必修2)》中没有证明这个定理，直到《数学(选修2-1)》中，才用空间向量证明了这个定理，但许多教师容易忽略这块内容.另外，可能也是受到了面面垂直性质定理的影响，因为在面面垂直的性质定理中，只要垂直于交线就得到线面垂直，说明考生没有真正理解该定理，从而造成了知识点的混淆.

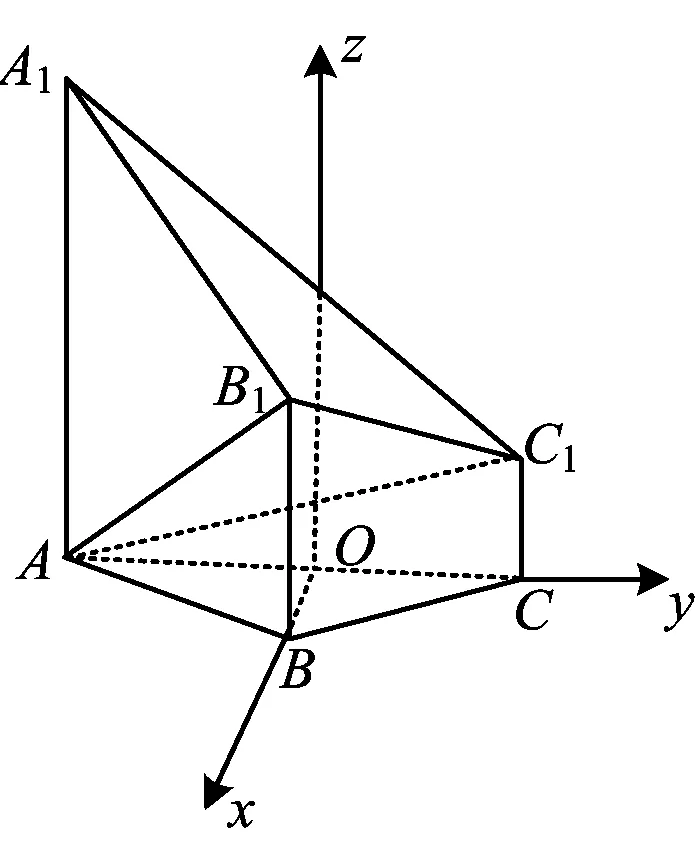
图2

证法2如图2，以AC中点O为原点，分别以射线OB，OC为x轴、y轴的正半轴建立空间直角坐标系O-xyz.

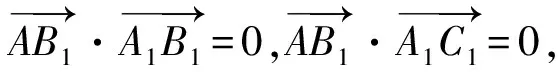
答题情况证法2与证法1类似，只不过换成了代数的形式解决立体几何问题，考生的错误也和证法1中的情况基本一致.在建立空间直角坐标系时，部分考生审题不清，误认为BA⊥BC，从而导致坐标完全错误.较证法1而言，证法2具有的优势是：即使建系错误的情况下，仍然可以利用过程和结论得分，甚至最高可以得4分.

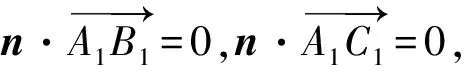
答题情况证法3与证法2类似，但是比证法2多了一个步骤，法向量与斜线所对应的方向向量平行，需要去验算这一步，因此错误也出现在这一步.有相当一部分考生都写成了数量积为0，而不是去证明共线，被扣了2分.如果知道是共线，那么运算就简单了.

图3

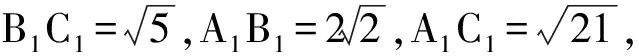
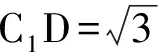
答题情况解法1是参考答案给出的方法，但在阅卷过程中发现，真正用这一方法的考生少之又少.其实命题者的意图，是希望通过第1)小题线面垂直对第2)小题有提示作用，这也符合浙江省命题者设计小题时层层递进的思路.而考生却忽略了该功能，同时也反映出考生对面面垂直性质定理不太熟悉，运用得不够熟练.

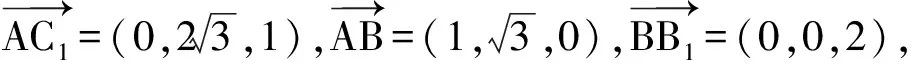
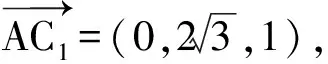
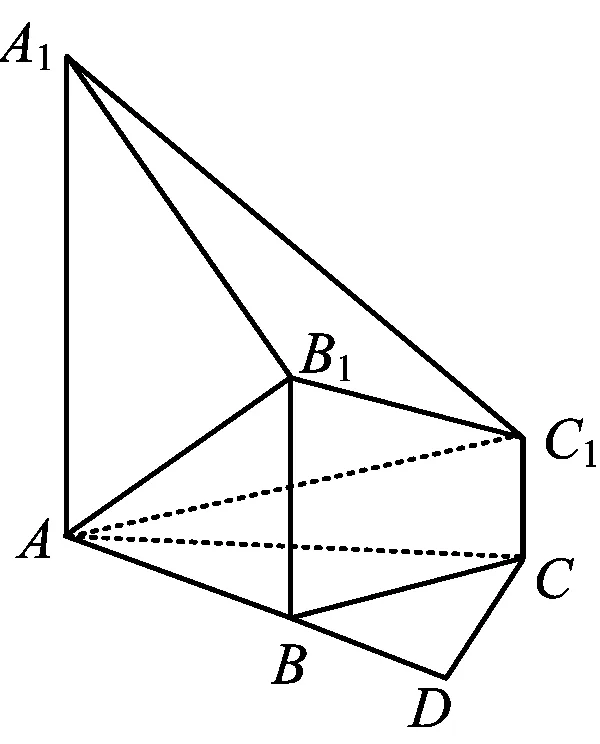
图4

根据建系位置的不同，得到的向量的坐标有些许区别，但评分标准得分点完全一致.

答题情况只要正确建立空间直角坐标系的考生，绝大多数都得到满分，只有极少数考生由于知识点混淆，画蛇添足，求出所谓的“正弦值”(其实是余弦值)，反而被扣了2分.

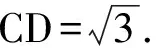
其中θ表示直线AC1与平面ABB1所成角的大小.

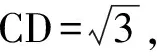
答题情况解法3与2017年浙江省数学高考试题第19题的方法一致.

由此可见，浙江省数学试题在命题过程中，都会有几年的延续性和一贯性[2]，深入研究高考真题、挖掘标准答案方法和渗透的思想非常重要.

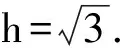
其中θ表示直线AC1与平面ABB1所成角的大小.

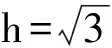
答题情况等体积法是往年文科生最喜欢用的一种方法，因为找不到线面垂直，就找不到垂足，所以等体积法就是解决线面角的最佳方法.但是，可能以往理科生很少用这种方法，从阅卷来看，考生用得还不是很多，但是用了的基本上都是正确的.

阅卷得分点补充说明：1)第2)小题的建系分数，坐标系正确并给出点的坐标或向量坐标，则得2分； 2)在第1)小题不正确的情况下，建立了正确坐标系给出建系分2分；3)不重复给分.

4 答题策略

基于上述标准答案和相应的得分点，不难发现：在第1)小题中，总共6分，其中不管用哪种证法，都是亮出相应的原理给2分，写出运算关键过程给2分，得到正确结论给2分；在第2)小题中，总共9分，也是不管用哪种解法，只要亮出相应的原理给2分，写出运算关键过程给3分，有关键点数据给2分，结论正确给2分.而且，每个得分点都是独立给分.

不管用哪种方法，每种方法都是对应给分，不偏袒任何一种方法和运算，只要考生理解知识点、会逻辑推理、熟练各种运算，只要体现出自己的高中数学核心素养，那么每懂一块内容、每用一次思想、每写一个步骤，都给相应的独立分，这就是得分点.体现出了“考知识，重推理，注运算，显素养”的原则，始终保持等值性、公平性.

笔者在阅卷过程中还发现：思维逻辑能力比较强的学生，往往推理过程写得很简洁，关键步骤都写在答卷上，易于分辨.但是部分考生逻辑思维混乱，写得密密麻麻，却不知所云，答题不在点上，导致失分.甚至，有部分考生已经答题了，而且很多关键点也答到了，但是又涂掉了，从而没有得分令人惋惜.

5 阅后感悟

1)考知识.老生常谈重视落实基础知识、基本技能、基本思想和基本活动经验，那么如何在课堂中落实四基是我们所面临的最大课题.针对空间向量与立体几何的教学，《普通高中数学课程标准(2017年)》(以下简称《新课标》)指出：“应重视以下两方面：第一，引导学生运用类比的方法，经历向量及其运算由平面向空间的推广过程，探索空间向量与平面向量的共性和差异，引发学生思考维数增加所带来的影响；第二，鼓励学生灵活选择运用向量方法与综合几何方法，从不同角度解决立体几何问题(如距离问题)，通过对比体会向量方法的优势.在上述过程中，引导学生理解向量基本定理的本质，感悟‘基’的思想，并运用它解决立体几何中的问题.”[4]

因此，利用类比和对比的方式，可以让学生对容易混淆的知识产生认知冲突，从而加强思维方法的能力.在批判和矛盾中，产生更强烈的思维冲突，从而达到固化的效果.

2)重推理.学习立体几何中有一个很重要的能力，就是逻辑推理能力.拥有良好的逻辑推理思维能力的学生，往往在答题步骤上非常简洁，也更容易得满分.反观逻辑思维混乱的学生，往往答不到点上，想到哪就写到哪，往往容易忘记初心——到底想要得到什么.

其实，《数学(选修2-2)》第二章内容就是推理与证明.但是很多教师都没有很好地重视该节内容，认为平时在课堂中已经潜移默化地学习了这些内容，没有单独拎出来让学生有个系统的认识，反而让很多学生失去了这个能力.因此，在高考复习中必须回归教材[3]，形成系统的知识建构，每块知识都有其相应的能力和思维的培养，让每块知识都发挥其应有的作用.

3)注运算.运算是浙江省历年高考数学卷的核心，包括立体几何试题.自从引进空间向量与立体几何内容之后，很多学生由于空间想象能力较差，毅然选择了解析几何代数法.但是近几年在考查该内容时，由于建立空间直角坐标系难度非常大，也容易产生建系错误.因此，运算可以更好地帮助学生注意到细节，华罗庚有句名言：数少形时缺直观，形少数时难入微.

4)显素养.《新课标》指出：“引导教学更加关注育人目的，更加注重培养学生核心素养……，为阶段性评价、学业水平考试和升学考试命题提供重要依据，促进教、学、考有机衔接，形成育人合力.”[4]因此，浙江省数学高考命题组在命题时，一定会考虑到结合高中数学核心素养.

而立体几何的核心素养主要体现了逻辑推理、直观想象、数学运算.由于学生个体存在差异，呈现“百花齐放”的现象，因此，在平时教学中，尽量要全面介绍各知识点，从而让学生有更多的选择，有些学生直观想象能力比较强，有些学生数学运算能力比较强，还有的学生比较均衡，甚至两种能力相结合，不管是运用了哪种能力，只要能达到最终的目的，就是达到了高中数学核心素养的要求.