通性通法都去哪儿了*
——一道质检题的解法分析及教学反思
●
(侯集高级中学,江苏 徐州 221121)
1 背景
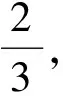
2 试题解析
例1已知函数
的图像恰好经过3个象限,则实数a的取值范围是______.
分析当a<0时,y=ax-1(其中x≤0)的图像经过第二和第三象限,而y=x3-ax+|x-2|>0在(0,+∞)上恒成立,从而图像仅在第一象限,因此当a<0时显然符合题意.当a≥0时,y=ax-1(其中x≤0)的图像仅经过第三象限,由题意y=x3-ax+|x-2|(其中x>0)的图像需经过第一和第四象限,等价于函数f(x)=x3-ax+|x-2|(其中x>0)有两个零点.以下使用3种方法分别求解:
方法1函数最值法.
f(x)=x3-ax+|x-2|=
则

1)当0≤a≤1时,
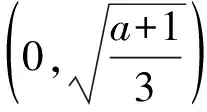
a无解.
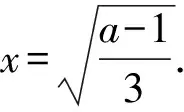
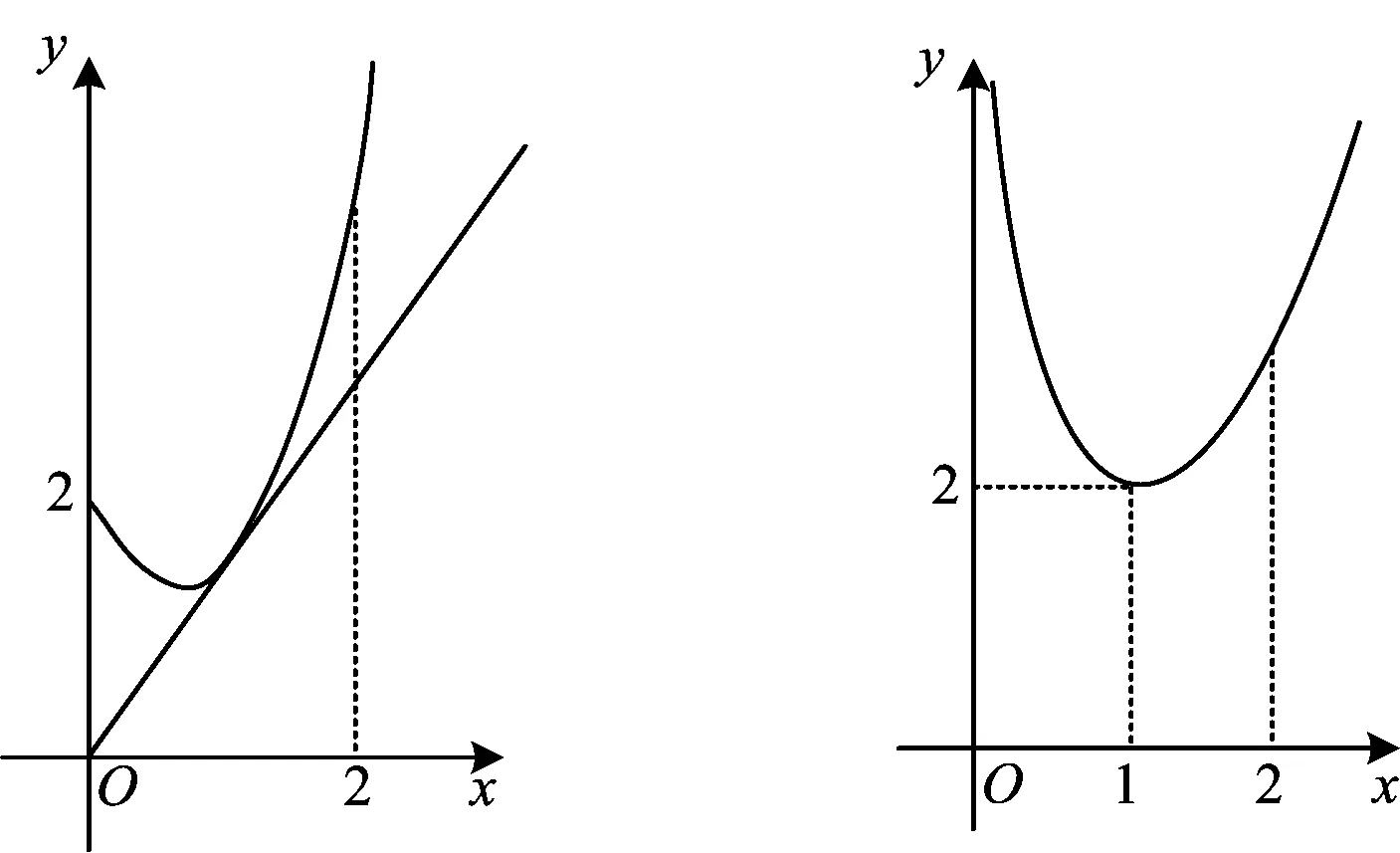
①当1 即可,解得2 ②当11 于是y=x3-(a+1)x+2在(0,2)上单调递减,y=x3-(a-1)x-2在[2,+∞)上单调递增.要满足题设,只需 f(x)min=f(2)=23-(a+1)×2+2<0 即可,解得11 ③当a>13时, 即可,解得a>13. 综上可得,a>2. 评注方法1是解决有解问题的最基本方法,其实质就是讨论函数极值点与分段函数的分界点的大小关系,从而确定函数的走势,进而得到函数的最值. 方法2数形结合. f(x)=x3-ax+|x-2|(其中x>0)有两个零点,即方程x3-ax+|x-2|=0(其中x>0)有两个解.问题可转化为g(x)=x3+|x-2|与h(x)=ax在y轴的右侧有两个交点. 则 作出g(x)的图像(如图1),设切点为(x0,y0),则 两者联立可解得x0=1,a=2,因此a>2. 评注该方法是将方程有两个解的问题转化为两个函数的图像有交点的问题处理.这两个函数的图像一直一曲,即直线和曲线有两个交点,因此先考查临界状态即相切的情况.这是利用导数的几何意义解题,从过程上看,显然比函数最值法有优势. 图1 图2 方法3分离参数. 将方程x3-ax+|x-2|=0的两边同时除以x,方程变形为 得 可以求得h(x)min=2,容易作出h(x)的图像(如图2),进而得到a>2. 评注解决恒成立、有解、零点的个数等问题,学生最喜欢的方法估计就是分离参数了.参变量分离后,函数不再“寄人篱下”,从含参中解放出来,成为了定函数,而参数成为了垂直于y轴的动直线,对于问题的解决,一目了然. 本题考查的是函数的零点个数问题.此类问题是高中数学的常见题型,对于经过了两轮复习的高三学生而言,本应是比较容易入手的.教师拿到试卷后,几乎一致认为:这是一道“熟题”,教师常讲,学生常做,运用的是通性通法,至少也能答对一二百人吧,甚至有些教师担心此题作为压轴题可能会“压不住”.但“理想很丰满,现实很骨感”,考试结果让人大跌眼镜:很多学生反映在考场上大脑一片空白,不知从何下手;另外一些学生即便是想到了解题的方法也因为种种原因半途而废.这让笔者不禁思考:为什么教师辛苦地教,学生卖力地学,得分的考生却寥寥可数,通法都去哪儿了?问题出在哪里?我们该如何解决? 1)通性通法的机械“植入”费时费力,放手给学生才是有效手段. 高中数学教学内容多、任务重、时间紧,因此很多时候教师在课堂上舍不得给学生独立思考解决问题的时间,而是滔滔不绝地一遍又一遍地讲.有时学生甚至题目还未读完,教师就开始频频“引导”;即便是思维比较活跃的学生在思考的过程中,也不断被教师所谓的“启发”所打断.结果,一些通性通法被生硬地“植入”到学生的头脑中,学生只能机械地解题,遇到新题、难题就抓耳挠腮,无所适从. 教学,既要教,也要学,更要教学生学.教是为学生创造条件,教是为了促进学,激发学,是为了加速学,但无论如何教不能代替学,没有学则教无意义[1].富兰克林曾说:告诉我,我会忘记;教给我,我可能记住;让我参与,我才能学会.点燃学生思维的火花比灌输给学生解题的方法更有效.比如在讲解本题时,笔者先进行调查,让学生大胆说出当时的想法以及思路遇到的障碍.“老师,我直接去绝对值讨论的(函数最值法),好像有点乱,搞晕了,没做完”,“我用的数形结合,太紧张了,结果搞反了”,“我想到了分参,但也不怎么确定,没敢做,时间也不太够”,“我看到这一题时,大脑一片空白,好大一会没有任何想法”,“对对对,我也是,什么法也想不到,根本没有思路”……学生们求助的眼神告诉了笔者,他们急需听到教师的讲解,笔者没有“心软”,决定残忍地“放手不管”.课堂上把时间还给学生,让他们去自主探究,并让学生上台展示,充分暴露学生的思维过程.即便是学生的板演出错,教师也不是“一擦了之”,而是鼓励学生大胆质疑,大家共同研究出错的原因,给出正解.其中部分学生思路中断的做法也由学生合作完成“续集”,然后大家谈感受、讲收获,最后总结解题经验、教训.教师作为组织者的角色出现在课堂,当学生研究出现困难时,教师也仅仅是“友情客串”.在整堂课的研究过程中,学生的积极性被充分调动起来,课堂参与度高,这些通性通法、解题思想扎根于学生的脑海里,这样的解题教学才是高效的. 2)浅层次的一题多练事倍功半,阶梯式的探究方能修得正果. 章建跃曾说:在通性通法的解题教学中,要使学生逐步养成从基本概念、基本原理及其联系出发思考和解决问题的习惯,这是发展学生思维能力的正道[2].如果学生不能很好地把握数学基本概念和思维,就很容易养成思维上的惰性.要使学生真正掌握数学本质,熟悉通性通法,变式教学是一种行之有效的方法.但是所谓的“一题多变教学”很多仅停留在低层次的题海“傻练”上,仅局限于对试题模式识别层面上的求解,学生在考场上遇到此类虽似曾相识却又较为复杂的问题时常无计可施.笔者认为阶梯式的、递进式的解题教学才是行之有效的,这需要教师引导学生经常对问题进行深入挖掘.本题有这样几个“拦路虎”:含参、绝对值、分段函数,求解时需要涉及函数与方程、转化与化归、分类讨论及数形结合等思想方法.如讲解此题时,也可以先由一个容易题入手: 1)函数f(x)=x3-ax+x-2(其中x≥2)有两个零点,则a的取值范围是______; 2)函数f(x)=x3-ax+|x-2|(其中x>0)有两个零点,则a的取值范围是______; 这样的教学设计层层递进,可以达到润物细无声的效果.之后再辅之以必要的跟进训练,学生就会感觉复杂题仅仅是增加了“豪华包装”而已,难题并不难.如果层层剥茧揭开这些“豪华包装”,那么此类问题就会迎刃而解.教学中学生思维的训练深度决定了考场上的解题能力,只有平时引导学生多进行阶梯式的研究性学习,才能提高学生创造性的解题能力,遇到新题难题能够临危不乱,冷静分析,准确作答.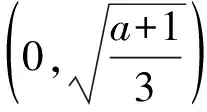
3 反思



