一个距离 五种视角*——基于直观想象的2018年浙江卷第9题感悟

●

(平湖中学,浙江 平湖 314200)

2018年的高考已经落下帷幕，浙江省高考数学试卷严格遵循了《2018年浙江省普通高中高考考试说明》(以下简称《考试说明》)中提出的“数学高考应具有较高的信度、效度、必要的区分度和适当的难度”.试卷严格按照《考试说明》中的“数学学科的考试要发挥数学作为基础学科的作用，既考查考生的基础知识、基本技能的掌握程度，又考查考生对数学思想方法、数学本质的理解水平以及进入高等学校继续学习的潜能”的考核要求进行命制.试卷对数学核心素养的考查更是比比皆是，笔者仅以选择题的第9题为例，谈谈对数学核心素养中的直观想象素养的精彩考查.

1 考题重现，品味经典

( )

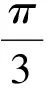
(2018年浙江省数学高考试题第9题)

本题是选择题的第9题，优秀学生必须要争取得满分，起着至关重要的作用.该题以向量为主要的考核知识点，向量因为其几何、代数双重身份而特殊，在中学数学中具有广泛的应用，因而地位十分重要，也成为高考重点考查的内容之一[1].试题以圆为背景，考查距离问题，对于圆的知识要点无论在人教A版《数学(必修2)》中第118页“圆的标准方程”，还是在第124页A组第5题“圆的直径式方程”中都考查得淋漓尽致.

2 解法探究，品尝思路

x2+y2-4x+3=0，

即

(x-2)2+y2=1，

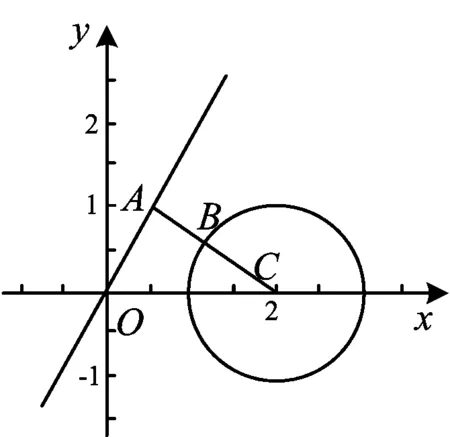
图1

从而平面向量b的终点B(x,y)是以C(2,0)为圆心、1为半径的圆(如图1)，过点C作CA⊥OA交⊙C于点B，于是

|a-b|min= |CA|-|CB|=

故选A．

点评考生在考场上是否想到利用坐标法进行研究向量终点的轨迹是解决此题的关键.通过坐标法求出向量b的终点B的轨迹是一个圆，然后把问题转化为圆上一点到射线上一点的距离问题，从而转化为圆心到射线的距离问题.这样的转化对于大部分考生来说应该都可以做到，也是非常有效的解法.

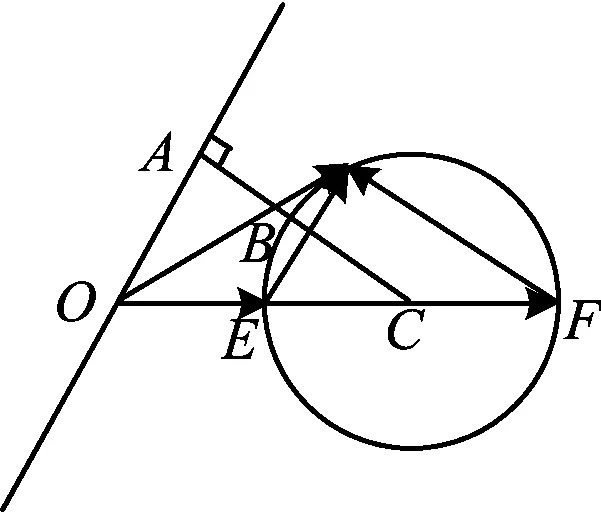
图2

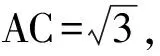
故选A．

点评该方法的关键是把常数3构造成3e2，从代数的角度来理解，类比于齐次式的想法，b2-4e·b可以看成是二次，3是常数，因此需要把3构造成3e2，然后写出两个向量数量积的形式.在考场上采用这样的方法需要比较丰富的解题经验和临场应变能力，具有较高的思维含量.

分析3(不等式视角)由b2-4e·b+3=0得

b2-4e·b+4e2=1，

从而

(b-2e)2=1，

于是

|b-2e|=1，

进而 |a-b|= |(a-2e)+(2e-b)|≥

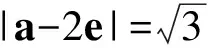
点评该方法的关键是要配成向量模的平方的形式，得出|b-2e|=1，接下来根据向量的三角不等式进行构造，从而把“两个动点的距离问题”转化为“一个定点与一个动点的距离问题”，解决起来会容易很多.在这个问题解决的过程中进行了两次放缩，因此还要检验等号是否都能够取到.

分析4(恒等式视角)由b2-4e·b+3=0，得

b·(b-4e)=-3.

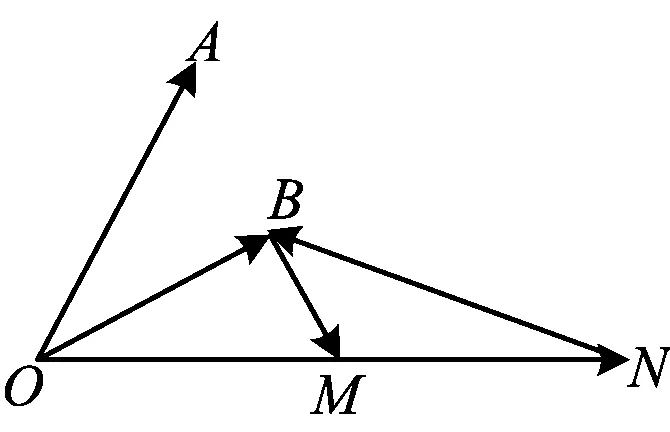
图3

由极化恒等式得

点评该方法先要转化成两个向量的数量积的形式，此时等式的右边刚好是常数.转化后的等式恰好可以看成是有共起点的两个向量的数量积为常数，这个形式非常容易想到极化恒等式，从而转化动点到定点的距离为常数.

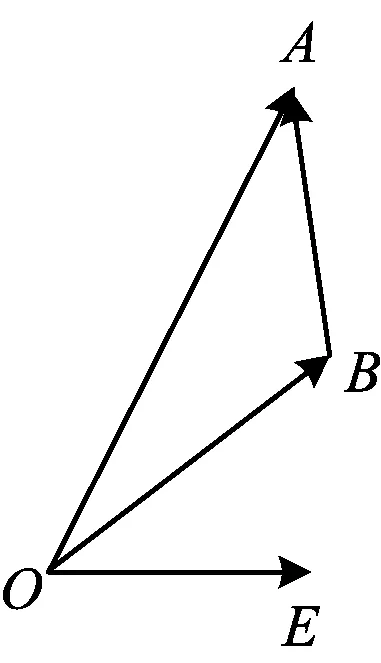
图4

分析5(代数视角)设e与b的夹角为θ，由b2-4e·b+3=0得

从而

由图4可知，当|a-b|取得最小值时，向量b在向量a与e之间，于是

令b2-5=t∈[-4,4]，则

点评该方法的入手是比较自然的，等式当中有两个变量：一个是向量|b|，另外一个是两个向量的夹角(或夹角的余弦值).要研究|a-b|min问题，可以考虑用两个变量之中的一个变量进行表示，转化为函数的形式，接下来可采用以下5种不同的处理方式来解决|a-b|min问题.

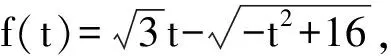
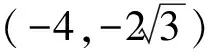
故

点评研究函数的最小值，既要知道函数的定义域，也要知道函数的单调性，而当已知定义域函数的单调性不能直接分析出来的时候，只有选择利用导数进行研究.在求导的过程中，既要清楚导数的运算量，也要知道复合函数的求导公式，还要在有效的时间内判断出导数的符号，但作为选择题这不是一种有效的处理方式.

处理2(三角换元)令t=4cosφ(其中0≤φ≤π)，则

点评三角换元的引进，首先要看到变量的有界性，联想到三角函数的有界性，对引进的角进行必要的限制，只要达到解决问题的目的即可.这样的处理方式，一个非常大的优势就是把根号去掉了，进而转化为求三角函数的最小值问题，计算量明显小了很多.

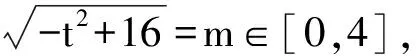
m2+t2=16.

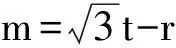
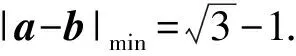
点评在这个题目中，根号的存在对于问题解决是一个较大的障碍.平方去根号是一种非常直接的处理方式，但是如果仅在原等式中进行平方是行不通的，因此需要引进一个新的变量，再进行平方，问题就转化为一条动直线和半圆的位置关系问题.

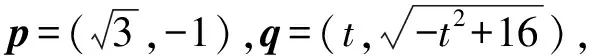
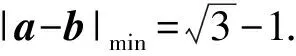
点评这样的处理来源于形式上的构造，这个形式刚好符合向量数量积的坐标形式，因此构造两个向量.本题构造向量的方式不止一种，比较有效的构造是一个向量是已知的，另一个向量的终点轨迹是比较熟悉的，此时代数式的最小值恰好可以通过图形观察出来.对于数学素养比较高的学生还可以通过构造柯西不等式进行解决，如：

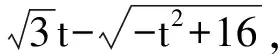
点评该方法通过引进两个变量，把一个等式转化为3个等式，虽然等式的个数增加了，但对问题的理解变得更加容易了，其中一个等式表示一条直线，另一个等式表示上半圆，问题转化为“圆上的点与直线上点当取得相同的横坐标对，纵坐标的差的最小值问题”.

3 源题追溯，品评联系

源头1已知向量a≠e，|e|=1，满足对任意t∈R，恒有|a-te|≥|a-e|，则

( )

A.a⊥eB.a⊥(a-e)

C.e⊥(a-e) D.(a+e)⊥(a-e)

(2005年浙江省数学高考理科试题第10题)

源头2已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则c的最大值是

( )

(2008年浙江省数学高考理科试题第9题)

( )

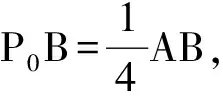
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

(2013年浙江省数学高考理科试题第7题)

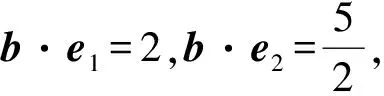
(2015年浙江省数学高考理科试题第15题)

4 教学启示，品鉴经验

2018年浙江省数学高考试题的第9题在关键的位置起到了关键性的作用，解决它的视角多、入手宽，使得不同数学素养的学生能够很好的区分，无论在解题时间上还是在解题效果上都达到了非常好的选拔功能.向量是几何与代数的交汇区，向量的运算有着浓厚的几何背景，数形结合的思想在平面向量中得到最充分的体现[2].通过这道考题的设置给我们的教学指引了更明确的方向.

4.1 挖掘教材，关注问题本质

在第9题平面向量的考查过程中，坐标法的视角来源于解析几何，利用圆的直径端点坐标来写圆的方程来源于教材的课后习题，向量的三角不等式来源于教材中的例题，同时实数的三角不等式在教材中也是有明确要求的，对于极化恒等式的模型在人教A版《数学(必修4)》的例题中有两处出现，在《数学(必修2)》的例题中也出现过一次.张奠宙教授曾经说过：“数学教学的有效性关键在于对数学本质的把握、揭示和体验.”这道考题无论从哪一个视角入手，都需要把两个动点的问题转化为一个定点和一个动点的问题，然后探讨出动点的轨迹.对于问题本质的揭示有很多的处理方式，考生需要考虑的问题是如何在较短的时间内揭示出问题的本质，因此，在日常的教学中要更多地引导学生进行深入的思考，同时辨别对于不同背景的问题该如何解决.

4.2 钻研考题，注重相互联系

自2004年以来，通过向量的模为背景进行考查的浙江省数学高考试题出现的频率是非常高的.在这些考题中，我们要认真钻研考查的背景及本质、入手的视角，以及考题之间的相互联系.比如2018年的这道向量考题，无论是试题的背景还是试题的解决办法，在往年的考题中都频繁出现，但是考查方法常考常新，都能够很好地体现试题的选拨功能.因此在钻研高考试题的过程中，既要探究试题本身的个性化内容，又要品味试题之间的共性，从而发挥试题应有的指导性作用.

4.3 培养能力，提升学科素养

2018年的这道向量考题，对于不同的考生来说，在考场上解题的效果是不一样的.有的考生可能根本没有办法入手，有的考生可能花费了较长的时间最后做出了正确答案，有的考生可能分分钟就把问题解决了.这就体现了学生的学习能力和考试能力，在能力的背后更多的是学生的数学学科素养的差异.这道考题无论从哪一个视角入手，都离不开直观想象核心素养的考查，这也要求我们在平时的教学中要经常关注数学的六大核心素养的渗透.在教学的过程中，要有勇气在数学成长的路上等一下学生，多陪伴一下学生，如此学生才可能成长得更快，数学之路才会走得更远.

总之，2018年的浙江省数学高考试题很好地体现了《普通高中数学课程标准(2017年)》中提到的“使学生掌握数学的基础知识、基本技能、基本思想，使学生表达清晰、思考有条理，使学生具有实事求是的态度、锲而不舍的精神，使学生学会用数学的思考方式解决问题、认识世界”.试卷更多地关注学生数学核心素养的考核，同时对教学的指导性更加明确，持久性更强.