某乘用车整车怠速抖动控制研究
程 林, 刘启华, 赵文杰, 刘 涛, 姜耀全, 张小虎, 卢伯聪
(上海汽车集团股份有限公司技术中心,上海 201804)
随着经济水平的提升和生活品质的改善,人们对于汽车考量的不仅是外观、动力、油耗、排放、安全等传统因素,很大程度上也离不开驾乘感、舒适性等主观因素。在整车性能指标中,NVH性能已经成为用户敏感度最高的指标之一[1]。随着汽车保有量的增加,交通堵塞状况日益严重,整车在怠速工况下的时间量显著增多,人们对于怠速状态下汽车的舒适性要求也随着提高。汽车怠速时人们最直观的感受就是整车的振动水平,若振动过大,就会造成明显的市场抱怨。许多主机厂的售后问题都与怠速抖动有关,抖动水平直接影响客户评价。整车怠速抖动不但容易引起客户的不舒适感,而且会造成零部件振动过大,寿命降低,因此整车怠速抖动问题的研究与优化具有较大的实际意义。
本文针对某整车怠速抖动问题,先是通过NVH测试方法分析抖动频率特征,然后通过模态分析方法进行动力总成悬置系统刚体模态试验,确认抖动根本原因,再应用整车16自由度CAE模型进行参数敏感度分析,进行悬置刚度参数优化,成功降低该整车的怠速抖动量级,对于整车怠速抖动问题的解决方法具有一定的参考意义。
1 整车怠速抖动问题
1.1 基本描述
整车怠速抖动问题,普遍采用主观评估和客观测试相结合的方法[2]。本文故障车冷车起动时,怠速转速较高(约1 100 r/min),没有明显的抖动问题;随着水温的升高,发动机转速逐渐降低,车内抖动增加明显;完全热机后(约700 r/min),抖动量级较大且持续存在,易引起抱怨。
1.2 振动频谱分析
在驾驶员座椅导轨处布置振动传感器进行测试(采用整车坐标系,汽车前后方向为X,左右侧向为Y,竖直向上为Z),测试结果显示-抖动频率为11.3 Hz。该型车怠速时,发动机热机转速680 r/min,发动机运转一阶频率为11.33 Hz,与抖动频率吻合。从振动频谱图中看出,座椅导轨X向振动最大,Z向振动其次(Y向量级较小,略),如图1所示。

图1 座椅导轨怠速振动频谱Fig.1 Spectrum of seat rail idle vibration
通常,对于整车怠速抖动这样的系统问题,需要分析振动源和传递路径[3]。首先分析振动源,动力总成是整车怠速时的主要振动激励源,发动机曲轴回转系统及变速箱输入轴系统的旋转不平衡是产生一阶振动激励的因素之一;发动机燃烧不均匀性是产生一阶激励的第二个因素。它们均对发动机本体施加相应的激励力,产生本体振动响应,进而通过悬置产生力作用在车身上,再进一步传递到车内,表现为整车怠速抖动现象。在发动机本体上布置振动传感器进行测试(整车坐标系),结果如图2所示。发动机的振动能量主要集中在二阶,符合四缸机正常工作燃烧时的二阶振动,一阶振动没有明显异常,由此判断该车抖动问题主要受结构传递路径的影响。对于动力总成旋转不平衡激励和燃烧不稳定性激励的机理和优化方法,将另文深入剖析。

图2 发动机怠速振动频谱Fig.2 Spectrum of engine idle vibration
2 悬置系统试验分析
2.1 刚体模态基本原理
动力总成悬置系统是动力总成隔振性能的关键环节[4]。对于怠速抖动等低频问题来说,安装动力总成的几个悬置显然是最主要的结构传递路径,因此需要对悬置系统进行分析,以进一步判断问题原因。该车动力总成采用三点悬置,可以把动力总成悬置系统视为一个具有三个弹性支撑的质量-刚度系统[5]。这个系统有六个自由度,分别为沿三轴方向的平动x,y,z和绕三轴方向的转动θx,θy,θz,系统六自由度坐标为:
[q]=[xyzθxθyθz]T
(1)
根据拉格朗日定理和虚功原理,可得悬置系统动力学方程为:

(2)
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;F(t)为激励力。
2.2 动力总成悬置系统刚体模态
一般动力总成悬置系统刚体模态频率在5~30 Hz之间,较易与发动机低阶激励耦合,悬置是否合理设计关系到整车对动力总成激励的敏感程度。采用试验模态方法测试各个测点加速度响应,并提取模态参数[6-7]。结果如表1所示。模态振型如图3~8所示。

表1 动力总成悬置系统刚体模态
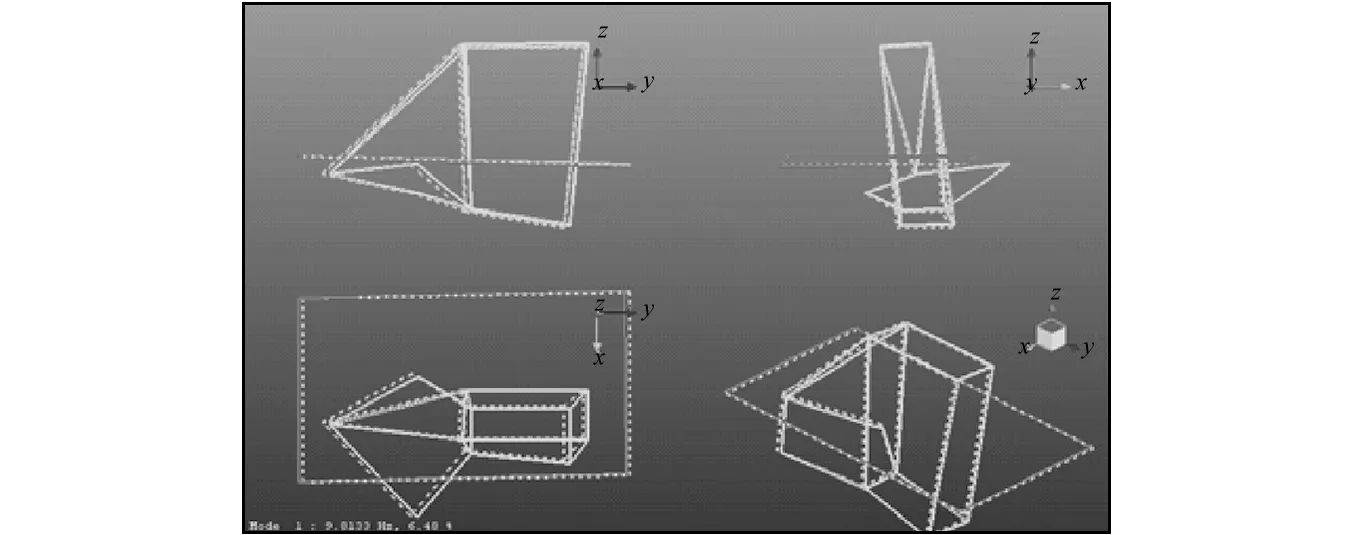
图3 第一阶模态振型Fig.3 The first mode
图4 第二阶模态振型Fig.4 The second mode

图5 第三阶模态振型Fig.5 The third mode

图6 第四阶模态振型Fig.6 The fourth mode

图7 第五阶模态振型Fig.7 The fifth mode
图8 第六阶模态振型Fig.8 The sixth mode
从结果中可以看出,Z向平动(Bounce)对应的第2阶刚体模态和X向平动(Fore-aft)对应的第3阶刚体模态这两个模态本身就比较接近,可能引起这Z向和X向这两个方向对应模态间的耦合。整车怠速下动力总成激励的一阶振动分量11.3 Hz,与Z向平动模态10.9 Hz和X向平动模态11.9 Hz均非常接近,极易引起耦合共振,从而造成整车抖动。从前面的分析可知,整车抖动时最显著的方向也是Z和X这两个方向。据此可以判断,该整车怠速抖动问题是由于悬置系统刚体模态与动力总成一阶振动分量耦合共振。
3 整车系统CAE分析
3.1 整车16自由度模型
悬置系统需要重新设计匹配来避开模态共振,一般改变悬置的安装位置、角度或刚度[8]。对于量产车来说,改变悬置的安装位置、角度显然相当困难,比较可行的是改变悬置的刚度。目前整车普遍采用三点或四点悬置,每个悬置有三个刚度方向参数,涉及变量较多。因此需要需要合理配置悬置参数,降低振动耦合度[9]。本文通过CAE仿真手段建立模型计算整车怠速抖动,基于悬置刚度偏差进行DOE仿真分析,同时对各个刚度参数进行敏感度分析,以确定每个方向刚度参数对于怠速抖动的影响程度。整车16自由度刚体模型如图9所示。

图9 整车16自由度CAE模型Fig.9 CAE model of vehicle with 16 freedoms
3.2 悬置刚度敏感度分析
该整车采用三点悬置,分别为发动机悬置,变速箱悬置和下系杆悬置,以悬置刚度为输入,以座椅导轨振动为输出。设定DOE工况输出限值如下:
f(K1,K2,K3)≤0.005
(3)
[Ki](Kix,Kiy,KiZ),i=1,2,3
(4)
式中:K1x,K1y,K1Z分别为发动机悬置三个方向刚度,K2x,K2y,K2Z分别为变速箱悬置三个方向刚度,K3x,K3y,K3Z分别为下系杆悬置三个方向刚度。
每个悬置3个方向共计9个变量,以这9个刚度变量为输入,共512个工况,以刚度上下浮动20%为设计因素变化量进行DOE计算,基于DOE结果对于各悬置三个方向刚度参数进行敏感度分析。设置悬置刚度与座椅导轨振动的关联程度方程如下:
(5)
式中:Rab表示关联程度;a为悬置刚度;b为座椅导轨振动。
由关联度计算可知,悬置刚度对座椅导轨振动的敏感度排序依次是下系杆悬置X向刚度,发动机悬置Z向刚度,变速箱悬置Z向刚度。座椅导轨两个方向振动与悬置刚度的关联度结果分别如表2和表3所示。
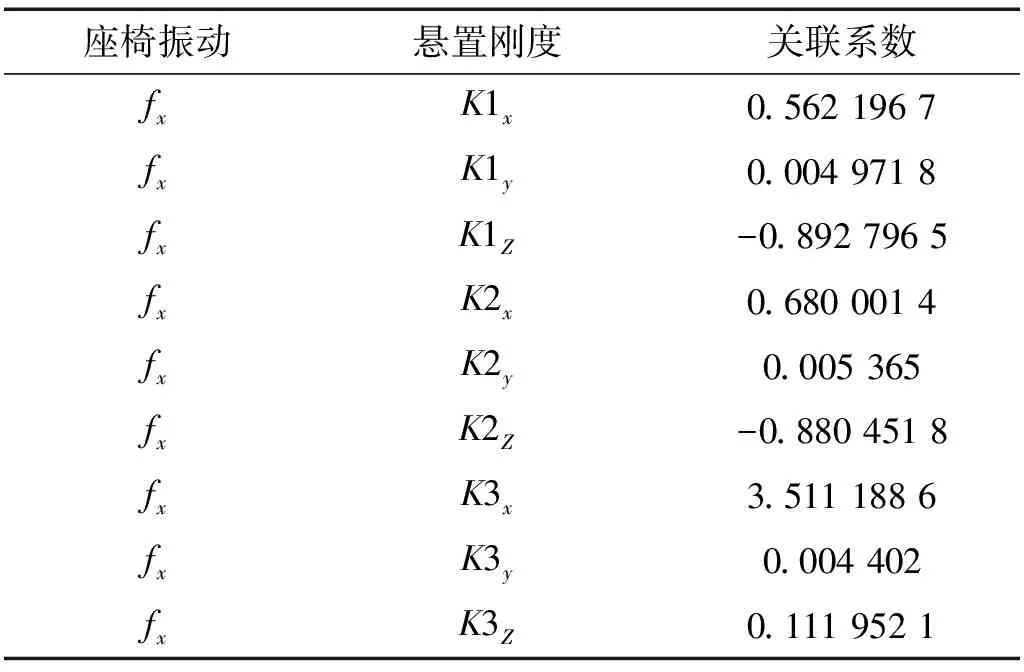
表2 座椅导轨X向振动与悬置刚度的关联度
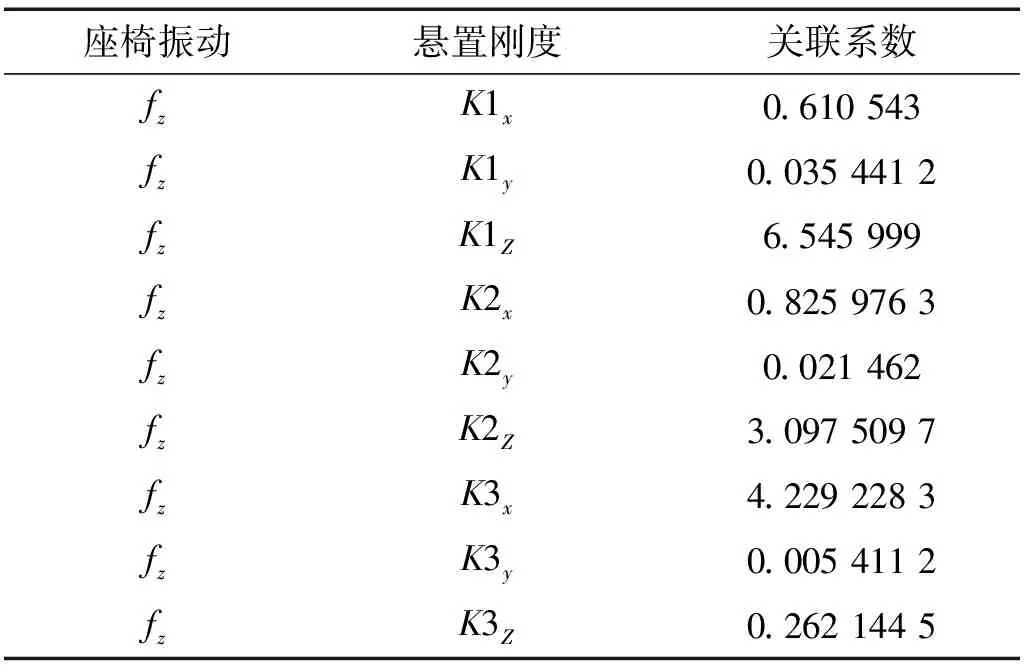
表3 座椅导轨Z向振动与悬置刚度的关联度
4 试验验证及结论
4.1 试验验证
在满足性能指标的前提下,敏感度高的设计变量应尽可能保持在最优值附近,设计、制造都要从严要求[10]。基于悬置刚度参数敏感度分析结果,控制下系杆X向刚度、发动机悬置Z向刚度和变速箱悬置Z向刚度在悬置零部件偏差在设计中值附近,对于三个悬置进行刚度优化。将改进后的悬置装车后进行试验验证,发现整车怠速抖动明显下降。客观测试显示,座椅导轨一阶抖动抱怨的频率亮带基本消失。优化后座椅导轨怠速振动如图10所示。

图10 优化后座椅导轨怠速振动Fig.10 Idle vibration of seat rail after optimization
对于悬置刚度优化后的车辆进行实车主观评估,以验证实际改善效果。实车怠速工况主观评估结果如表4所示。

表4 怠速工况主观评估结果
由上述可知,悬置刚度优化对于怠速工况振动有明显改善,但不确定优化后对于瞬态工况(特别是加速工况)的影响,因此还有必要评估下优化对于其他工况整车振动的影响。该车为自动挡,仅需评估D挡加速。D挡加速工况主观评估结果如表5所示。结果表明,优化对于其他工况整车振动无恶化。

表5 D挡加速工况主观评估结果
4.2 结 论
(1)运用模态测试方法获取动力总成悬置系统的刚体模态信息,分析怠速抖动原因,为类似怠速抖动问题研究提供了思路。
(2)采用CAE仿真手段建立整车16自由度刚体模型,针对悬置刚度参数进行敏感度分析,为怠速抖动优化提供了方向。
(3)将刚度参数优化后的悬置装车验证,发现优化后怠速抖动明显改善,对于整车怠速抖动问题的解决具有参考价值。

