基于改进均匀设计响应面的桥梁地震易损性分析
李辉辉, 李立峰,2
(1. 湖南大学 土木工程学院 长沙 410082; 2. 湖南大学 风工程与桥梁工程湖南省重点实验室,长沙 410082)
地震易损性分析是一种常用的概率性地震风险评估分析工具,可以反映结构在不同强度地震动作用下,其地震需求达到或超过指定损伤状态的条件概率。地震易损性分中不确定性因素主要来源于地震波、结构和材料等方面,忽略这些不确定性的影响,可能会对桥梁结构的抗震性能造成不合理评估[1]。为此,国内外学者对各类不确定性对结构抗震性能的影响作了大量的研究,如Jernigan等[2]、Hwang等[3]和Pang等[4]。由于各类不确定性因素的存在,结构地震易损性函数通常具有高维非线性特征;另外,目前求解易损性函数一般要转化为计算失效概率的高维非线性数学积分问题,这使得对易损性函数直接积分计算具有巨大的困难。为解决这一问题,学者们提出了许多近似方法,如贝叶斯方法[5]、条件边缘概率法[6]和响应面法[7]等。其中,响应面法由于原理简单而得到了广泛应用。结构响应面模型的建立主要包括三个关键问题:①试验设计,即确定样本点和结构响应值;②选择满足结构功能函数的响应面模型函数,其中以二次多项式[8]运用最广;③响应面函数拟合与模型精度验证。
首先,对于试验设计,为减少试验样本和保证计算精度和效率,许多学者尝试采用均匀设计[9]来拟合响应面。例如,吕大刚等[10]在研究钢框架结构抗震可靠度分析问题时,分别从计算效率和求解精度方面比较了均匀设计响应面法和Monte Carlo等方法的有效性,其研究结果表明:均匀设计响应面法不仅可以明显减少试验样本量,并且其构造的极限状态函数可更好拟合结构功能函数曲面,得到的可靠度分析结果和Monte Carlo比较相近;胡常福等[11]在对一索拱桥进行非线性索力优化研究时,从主拱圈弯矩优化结果和优化迭代次数等方面比较表明,其提出的基于均匀设计响应面法和牛顿迭代法相结合的索力优化方法可明显减少试验样本和优化迭代次数,在索拱桥非线性索力优化分析中有较好的适用性。然而,尽管均匀设计可大幅度减少试验样本而不失抽样精度和计算效率,但小样本数据之间通常会存在多重相关性现象,进而使得模型的准确性和可靠性难以得到保证[12]。其次,对于响应面函数形式的选取,通常采用非线性模型更为合理,然而在处理非线性问题时,往往需要通过变量代换将非线性模型转化为线性模型分析,这一函数变换过程会使变量维数增加,且变换后的设计变量之间会重新产生多重相关性。由于以上两个关键问题均可能产生多重相关性,在拟合响应面时,若继续通过传统的最小二乘回归分析可能会导致模型计算不收敛或者产生较大舍入误差,为此,本文采用偏最小二乘回归代替最小二乘回归来解决这一问题。
另一方面,以往大量地震易损性研究,为了分析的简便,通常假设各种不确定性随机变量相互独立,而考虑变量相关性对地震易损性分析影响的研究较少。然而,在实际工程中,结构的材料特性和力学特征往往是统计相关的,忽略结构参数等随机变量相关性条件的影响,可能会高估桥梁结构在特定强度地震动作用下的易损程度。为此,有必要对地震动、结构参数等随机变量间的相关性对桥梁结构地震易损性分析的影响进行研究。
对于随机变量之间相关性的处理,国内外学者做出了一定的研究。Liu等[13]在研究结构可靠度问题时,首次提出了Nataf变换后的等效相关系数的经验计算公式,推广了Nataf变换在处理随机变量相关性问题的适用性;吴帅兵等[14]建议在处理相关非正态变量的结构可靠度计算问题时,应该考虑映射变换时相关性的变化,宜优先采用Nataf变换;吴帅兵等[15]比较了Orthogonal变换、Rosenblatt变换和Nataf变换的优缺点、适用范围及其对结构可靠度的影响,验证了Nataf变换在结构可靠度分析同时具有计算精度高和适用范围广的优点,建议在处理变量相关变换时宜优先采用。以上研究均表明,忽略变量相关性,会对结构可靠度分析有较大影响,并且Nataf变换是一种高效、合理解决随机变量相关性问题的方法。
为研究传统均匀设计响应面法中设计变量间的多重相关性现象和结构参数随机变量相关性对桥梁地震易损性分析的影响,本文首先简单介绍基于改进均匀设计响应面法的桥梁地震易损性分析流程;然后,以一多跨连续梁桥为研究对象,建立其精细化全桥非线性有限元模型,通过Nataf变换来处理结构参数随机变量相关性,采用均匀设计构造“桥梁-地震动”样本对,并以支座位移、墩底截面曲率和桥台位移等为桥梁结构响应,建立结构响应面模型;同时考虑墩柱、板式橡胶支座、铅芯橡胶支座和桥台四类构件的地震损伤,分别在考虑变量相关性前后、采用传统及改进均匀设计响应面法对算例桥梁地震易损性分析进行了比较,最后得出相应结论。
1 基于改进均匀设计响应面法的地震易损性分析
1.1 基于样条变换的均匀设计响应面法
响应面方法通过结构响应与设计变量之间复杂的隐式函数来近似拟合结构极限状态函数曲面,是一种试验设计与数理统计相结合的方法。传统均匀设计响应面法的基本原理可见文献[11],由于该方法需要预先假定特定形式的响应面函数,故阻碍了其进一步的工程应用。同时,在实际工程中,结构功能函数形式通常未知,并且具有高维非线性特征,预先假定响应面函数形式会产生较大误差,这种情况下,可将功能函数考虑为设计变量之间的加法模型[12]:
y=f1(x1)+f2(x2)+…+fp(xp)+ε
(1)
根据拟线性回归思想,可将式(1)中的设计变量函数fi(xi)进行变量替换,转化为拟线性回归模型,而实际工程中fi(xi)通常未知,模型仍不能求解。为此,可以采用数值分析理论中的样条基函数来对fi(xi)进行函数逼近,即选取样条基函数fi(xi)≈φi(xi),从而,式(2)可转化为:
y=φ1(x1)+φ2(x2)+…+φp(xp)+ε
(2)
样条基函数由多个分段多项式组合而成,而实际应用最广的为三次B样条基函数[16],其展开式为:
(3)

(4)
最后由偏最小二乘回归确定待定系数BPLS,确定结构响应面模型。评估式(4)所建立的响应面模型精度,可通过拟合系数R2来检验,可表示为:
(5)

1.2 Nataf变换
Nataf变换是根据一组相关随机变量的联合累积分布函数、相关系数矩阵和基于特征值分解的线性变换。若已知一组相关非正态分布随机变量组X=(X1,X2,…,Xn)T,其联合累积分布函数为FX(x),相关系数矩阵ρ=(ρij)m×n。其中,变量Xi和Xj的相关系数ρij可通过式(6)计算:
(6)
式中:μxi和σxi分别为变量Xi的均值和标准差;μxj和σxj分别为变量Xj的均值和标准差;E[·]表示期望值函数。变量Xi的边缘累积分布函数为FXi(Xi),根据等概率变换原则有:
Φ(Yi)=FXi(Xi)
(7)
式中:Yi为标准正态分布随机变量。从而变量Xi和Yi存在以下关系:
按照国家标准GB/T 19478—2004进行固始鸡的屠宰和样品的提取,测定不同样品中氨基酸组成及含量。
Yi=Φ-1[FXi(Xi)],Xi=FXi-1[Φ(Yi)]
(8)
式中:Φ-1(·)和FXi-1(·)分别为标准正态分布累积分布函数和Xi边缘累积分布函数的反函数。由式(7)和式(8)可将变量X变换为一组相关的标准正态分布变量Y,并且其联合概率密度函数存在以下关系:
(9)
式中:φn(y,ρ0)表示变量Y(相关系数矩阵为ρ0=(ρ0ij)n×n)的联合概率密度函数。由相关系数的定义、式(3)和式(4)可得变量X的相关系数ρij与其等效标准正态变量Y的相关系数ρ0ij有以下关系:
(10)
式中:φ2(yi,yj,ρ0ij)为相关系数为ρ0ij的二维标准正态分布联合概率密度函数。当变量Xi和Xj的边缘分布函数及相关系数ρij已知时,可以通过求解式(10)来确定其等效相关系数ρ0ij。然而,在求解式(10)所示的非线性方程组时,其求解过程非常复杂,并且当ρij接近于1或者-1时,ρ0ij可能无解。为此,Liu[13]通过最小二乘法给出了10种常见边缘分布的经验计算公式:
ρ0,ij=Fρij
(11)
式中:系数F≥1,与变量的分布类型、相关系数和变异系数有关。变量Y的相关系数矩阵是一对称正定矩阵ρ0=(ρ0ij)n×n,可对其进行Cholesky分解得下三角矩阵L,左乘L的逆矩阵L-1即可将Y转化为独立的标准正态变量Z。
Z=L-1Y
(12)
基于上述Nataf变换原理,可将一组相关随机变量组X变换为独立标准正态分布变量组Z,进而可对Z进行均匀设计来构造试验样本。
1.3 地震易损性分析原理
易损性曲线能够直观反映不同强度地震荷载作用下,结构地震响应达到或超过特定损伤状态的条件概率,可表示为如下形式:
Pf=P(D≥C|IM=x)
(13)
式中:P(D≥C|IM=x)表示结构在强度为IM=x地震动作用下地震需求(D)达到或超过其抗震能力(C)的概率;IM为地震动指标(Intensity Measure)。由式(13)可知,地震易损性分析包括两个重要内容:①结构概率地震能力分析 (PSCA),明确结构在不同损伤状态下的能力损伤模型,即确定结构地震能力C与IM的关系;②结构需求概率分析(PSDA),即确定结构地震需求D与IM之间的关系,可通过结构的概率地震需求模型(PSDM)来反映。既往研究表明,易损性分析中通常假定结构的抗震能力和地震需求服从对数正态分布,并且假定结构地震需求均值SD可表示为IM的指数函数[17],从而易损性函数可表示为:
(14)
式中:Φ(·)为标准正态分布函数,SD和SC分别表示结构地震需求和能力均值,βD|IM和βC分别需求和能力对数标准差。a和b表示SD和IM之间指数函数的回归系数。式(14) 可继续简化为:
(15)
式中:IMm和ξ分别表示在桥梁在不同损伤状态下的地震动强度中值和对数标准差。根据基于样条变换的均匀设计响应面法、Nataf变换和地震易损性分析原理,本文提出的基于改进均匀设计响应面的桥梁时变地震易损性分析流程图,如图1所示。

图1 基于改进均匀设计响应面的桥梁地震易损性分析流程Fig.1 Framework of bridge seismic fragility analysis based on the improved uniform design-response surface method
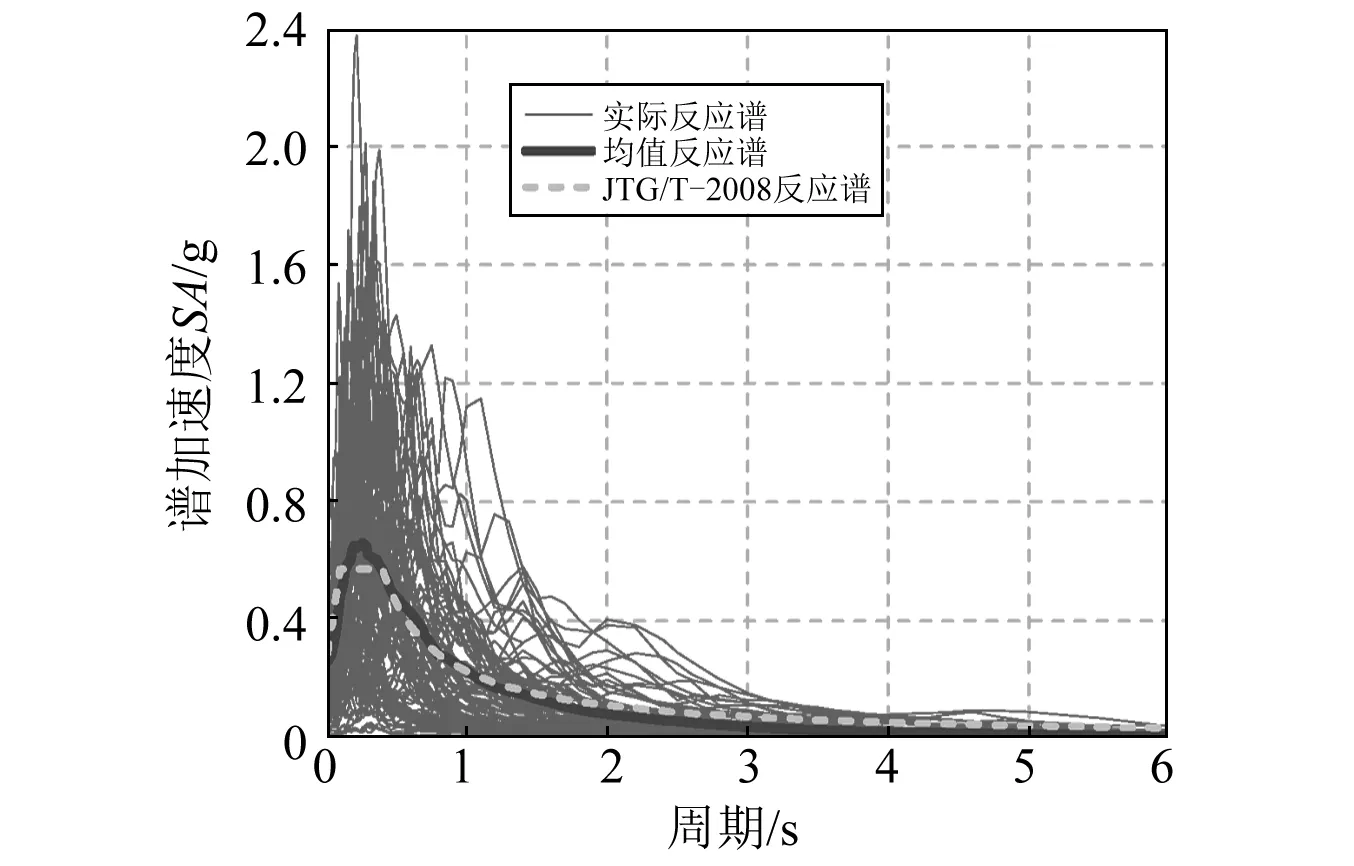
图2 地震波反应谱Fig.2 Response spectrums of ground motions
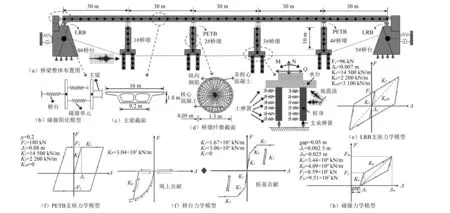
图3 算例桥梁有限元模型及构件力学模型Fig.3 Finite element model of the case-study bridge and mechanical model for bridge components
2 桥梁算例
2.1 工程背景及有限元建模
算例桥梁为一座跨径布置为5×30 m的钢筋混凝土连续梁桥,主梁为C50混凝土箱梁,梁高1.8 m;盖梁采用C40混凝土;桥墩为直径1.4 m的C30混凝土圆形墩,墩高10 m,纵筋和箍筋均采用HRB335钢筋,纵筋配筋率为1.08%,体积配箍率为0.58%,纵筋直径为28 mm,箍筋直径为10 mm,混凝土保护层厚度为50 mm;另外,两岸桥台为桩基支承的座式桥台;桥墩盖梁处采用板式橡胶支座(PETB),桥台处采用铅芯橡胶支座(LRB);桥墩盖梁和桥台处在横桥向布置了滑移混凝土挡块。
基于OpenSees源代码分析平台[18]建立桥梁非线性动力有限元模型。其中,桥梁上部结构采用弹性梁单元模拟;墩柱采用弹塑性纤维梁柱单元模拟,核心混凝土和非核心混凝土采用Concrete 04材料本构,且忽略混凝土材料的受拉性能,纵向钢筋采用Steel 02材料本构(在OpenSees程序中,Concrete 04本构,可通过定义混凝土峰值强度、屈服强度及各自对应的应变等参数来定义;Steel 02本构,可通过定义钢筋屈服强度、弹性模量和硬化比来定义,在本文桥梁基准有限元模型中,以上参数取为均值,如表1所示);桩-土相互作用采用等代土弹簧模拟,弹簧刚度依据我国公路桥梁抗震细则[19]进行计算;板式橡胶支座(PETB)和铅芯橡胶支座(LRB)均采用OpenSees数据库中的Elastomeric Bearing(Plasticity)Element模拟;桥台考虑了台后填土和桩基的贡献,可通过Hyperbolic Gap Material和Hysteretic Material来共同模拟;挡块采用滑移型混凝土挡块,通过Hysteretic Material和Elastic-Perfectly Plastic Gap Material两种材料模拟;桥台处的碰撞效应采用Aviram等[20]提出的简化弹簧系统,可采用Impact Material模拟。桥梁非线性动力有限元模型及各桥梁构件的力学模型,如图3所示。另外,地震波仅考虑纵桥向输入。

表1 结构参数随机变量及其分布特征
2.2 结构响应及设计变量的确定
为考虑桥梁结构和材料的不确定性,本文参考文献[21],共选取了11个结构参数变量作为设计变量,其中核心混凝土4个参数:峰值强度fc,core,峰值强度对应的应变εc,core,屈服强度fcu,core,屈服强度对应的应变εcu,core;保护层混凝土3个参数:峰值强度fc,cover,峰值强度对应的应变εc,cover,屈服强度对应的应变εcu,cover;纵向钢筋3个参数:弹性模量Es,屈服强度fy,钢筋硬化比γ;桥墩几何参数:桥墩直径d。结构参数分布特征如表1所示,取支座位移、墩底截面曲率和桥台主动及被动方向位移为桥梁结构响应。此处称表1中11个结构参数为相关变量组X,由文献[21]和式(6)可确定其相关系数矩阵ρ,如表2所示。根据Nataf变换可将变量组X转化为独立的标准正态变量组Z,然后对Z进行均匀设计(本文采用均匀设计表U50(5013)),与选择的实测地震动记录进行随机组合,从而可建立“桥梁结构-地震动”样本对。
2.3 地震波输入和结构损伤指标
合理的IM对减少结构响应预测的离散性有重要意义,既往研究表明,地震荷载作用下,规则梁桥地震响应主要由第一阶模态控制,并且考虑IM的效率性、实用性和充分性时,PGA并不是理想IM,而谱加速度SA更适合作为规则桥梁的IM[21],故本文以算例桥梁基本周期对应的谱加速度SA作为IM。为充分考虑地震动不确定性,本文根据桥梁场地条件类型,从美国太平洋地震工程研究中心(PEER)地震动数据库中选取了50条实测地震动记录,其反应谱曲线如图2所示。
根据桥梁结构损伤程度不同,可将桥梁损伤状态划分为:①轻微损伤;②中等损伤;③严重损伤;④完全破坏。本文基于变形破坏准则,并根据Nielson[17]的研究,假定轻微损伤和中等损伤对应的对数标准差取为0.246 2,而严重损伤和完全破坏对应的损伤指标对数标准差为0.472 4,依次定义了墩柱、板式橡胶支座(PETB)、铅芯橡胶支座(LRB)和桥台在地震作用下各损伤状态下的损伤指标如表3所示。其中,SC为结构抗震能力均值,βC为对数标准差;μφ为墩柱截面曲率延性比;μz为PETB位移延性比;γa为LRB容许剪切应变;δactive和δpassive分别表示桥台主动和被动方向变形。

表2 结构参数变量相关系数表

表3 桥梁构件损伤指标
3 地震易损性分析
在结构概率地震能力及需求分析的基础上,由式(15)计算各桥梁构件在不同地震动水平下的损伤超越概率,建立其在不同损伤状态下易损性曲线如图4所示; 另一方面,桥梁是由不同构件组成的复杂组合体系,仅从构件层次易损性分析不足于全面评估桥梁整体抗震性能,故有必要进行系统易损性分析。因篇幅所限,并且既往研究[22]表明,在地震荷载作用下,桥梁系统的损伤超越概率往往要大于桥梁构件,为此,本文基于前文提出的桥梁地震易损性分析框架,在不同桥梁构件联合概率需求模型(JPDSM)的基础上,通过Monte-Carlo方法建立系统在不同损伤状态下的易损性曲线,如图4所示。

图4 桥梁构件及系统地震易损性曲线Fig.4 Seismic fragility curves of different bridge components and bridge system
由图4可以看出:①桥梁构件在各损伤状态下的损伤超越概率均随着谱加速度SA的增大而增大;②对于前三种损伤状态,LRB是最易损伤的构件,而PETB的损伤超越概率则明显小于LRB,其主要原因是算例桥梁的桥墩侧向抗推刚度小于桥台刚度,使LRB的相对位移要小于PETB;③从图4(d)可注意到,LRB在完全破坏状态下损伤超越概率要小于PETB,这是因为此时LRB损伤不是由支座本身的破坏决定,而是由落梁破坏决定的,这在以后的桥梁抗震设计中应引起重视;④尽管桥墩在轻微损伤状态下的失效概率稍微大于设置于其顶部的PETB的失效概率,但在后三种损伤状态下,桥墩的易损性均小于PETB,这说明在以后对连续梁桥进行抗震设计时,可通过改善墩顶处支座滑移来减小墩柱的损伤;⑤桥台在地震荷载作用下发生严重损伤和完全破坏的概率较小,另外,值得注意的是,桥台在严重损伤和完全破坏状态下的易损性曲线较平坦,这可能是由桥台处复杂非线性碰撞效应使桥台地震响应离散性较大所引起的。⑥对于前三种损伤状态,地震荷载作用下,桥梁体系比单个构件更易破坏,仅用结构中最易损伤的LRB和墩柱等构件来评估桥梁系统易损性,通常会高估桥梁整体的抗震能力;另外,值得注意的是,在图4(d)中,PETB失效概率甚至大于桥梁体系,这可能是由于桥台处LRB损伤使桥梁发生落梁破坏,从而PETB可能在桥梁已经破坏之前还未完全破坏,因此,在实际的桥梁抗震设计中,可严格按规范[19, 23]在桥台处设置足够长的搭接长度,来避免落梁破坏,并且可通过减小LRB的滑移来改善桥梁的抗震能力。
4 基于传统与改进均匀设计响应面的易损性分析比较
由以上分析可知,本文提出基于改进均匀设计响应面的地震易损性分析框架,在处理考虑随机变量相关性的桥梁地震易损性分析中有较好的适用性。为探讨本文方法在地震易损性分析方面的有效性,分别从响应面模型精度、桥梁地震易损性曲线等方面对以下四种方法进行了比较:①考虑变量相关性的改进均匀设计响应面法(IUD-RSM-C),即本文方法;②不考虑变量相关性的改进均匀设计响应面法(IUD-RSM-R);③考虑变量相关性的传统均匀设计响应面法(UD-RSM-C);④不考虑变量相关性的传统均匀设计响应面法(UD-RSM-R)。
4.1 响应面模型精度比较
结构响应面模型精度可通过拟合系数来检验(与1越逼近表示响应面模型精度越高,所构造响应面能够更好地拟合结构功能极限状态函数),表4给出了四种不同方法的结构响应面模型拟合系数比较情况。

表4 四种方法结构响应面模型拟合系数比较
由表4可知:四种方法建立的结构响应面模型拟合系数均大于0.9,满足响应面模型精度要求,并且与其他三种方法相比,本文方法建立的结构响应面模型精度较好;分别由本文方法与IUD-RSM-R、UD-RSM和UD-RSM结果对比可知,考虑变量相关性条件影响后,结构响应面模型精度有一定程度地改善(最大增幅为分别4.39%),进而建立的结构响应面可以更好的对结构极限状态函数曲面进行拟合;与传统均匀设计响应面法相比,采用改进均匀设计响应面法所建立的响应面模型精度有一定程度提高(最大增幅为6.16%);值得注意的是,由IUD-RSM-R和UD-RSM-C结果对比可知,即使考虑变量相关性条件的影响以后,传统均匀设计响应面法建立的结构响应面模型精度仍然差于不考虑变量相关性的改进均匀设计响应面法,这可能是由传统均匀设计响应面中设计变量多重相关性现象所导致的。
4.2 易损性曲线的比较
分别通过前文四种方法进行易损性分析,由本文第3节内容可知,LRB和PETB支座为易损伤构件、而墩柱是桥梁重要构件,同时因篇幅所限,图5仅给出了这三种构件的易损性曲线对比情况;图6则给出了桥梁系统在不同损伤状态下的易损性曲线比较情况。
由图5可知:四种方法得到桥梁构件在不同损伤状态下易损性曲线变化趋势相同,但在相同地震动强度作用下,各桥梁构件发生破坏的损伤超越概率存在一定差异。分别由本文方法与IUD-RSM-R、UD-RSM和UD-RSM结果对比可知,考虑变量相关性条件影响后,桥梁构件在不同损伤状态下的损伤超越概率有一定程度的降低,最大降低幅度约为12.90%,例如,在图5(c)中,在谱加速度SA为0.6 g的地震动作用下,本文方法、IUD-RSM-R、UD-RSM-C和UD-RSM-R得到的LRB支座发生严重损伤的损伤超越概率分别为55.85%、58.89%、63.77%和68.75%,进而说明忽略变量相关性条件的影响,可能会高估桥梁构件的易损程度;分别对本文方法与UD-RSM-C、IUD-RSM与UD-RSM结果对比可知,与传统均匀设计响应面法相比,采用改进均匀设计响应面法得到的各桥梁构件在不同损伤状态下发生相同损伤超越概率的破坏所需的地震动强度SA有所增加,最大增加幅度约为15.88%,例如,在图5(a)中,墩柱在轻微损伤状态下,本文方法、IUD-RSM-R、UD-RSM-C和UD-RSM-R所得到的发生50%损伤超越概率对应的谱加速度SA值分别为0.488 g、0.480 g、0.472 g和0.464 g,这表明在对桥梁结构进行易损性分析时,采用传统均匀设计响应面法可能会高估桥梁构件的易损程度。

图5 不同方法桥梁构件易损性曲线比较Fig.5 Comparison of bridge components fragility curves for different methods

图6 不同方法桥梁系统易损性曲线比较Fig.6 Comparison of bridge system fragility curves for different methods
同理,和桥梁构件易损性曲线比较情况相似,由图6可以看出,四种方法得到桥梁系统在不同损伤状态下易损性曲线变化趋势相同,但在相同地震动强度作用下,桥梁系统发生破坏的损伤超越概率有所不同。由本文方法与UD-RSM-C、IUD-RSM-R和UD-RSM-R结果对比可知,采用改进均匀设计响应面法得到的桥梁系统在不同损伤状态下发生相同损伤超越概率的破坏所需的地震动强度SA值有所增加,最大增加幅度约为18.69%,例如,在图6(b)中,桥梁系统在中等损伤状态下,本文方法、IUD-RSM-R、UD-RSM-C和UD-RSM-R所得到的发生50%损伤超越概率对应的谱加速度SA值分别为0.402 g、0.387 g、0.390 g和0.385 g,这说明在对桥梁结构进行易损性分析时,采用传统均匀设计响应面法可能会高估桥梁系统的易损程度。另外,由本文方法与IUD-RSM-R、UD-RSM-C和UD-RSM-R结果比较可知,与不考虑变量相关性相比,考虑变量相关性条件影响以后,桥梁系统在不同损伤状态下的损伤超越概率均有一定程度的降低,最大降低幅度约为10.92%。因此,综合以上分析,在对桥梁进行地震易损性分析,采用传统均匀设计响应面法和忽略变量相关性条件的影响,均可能会高估桥梁结构的易损程度,从而不能对桥梁抗震性能进行合理评估,在实际工程应用中需引起足够重视。
5 结 论
(1)通过 Nataf 变换考虑结构参数变量相关性,本文方法能综合考虑地震动和结构的不确定性,在桥梁地震易损性分析中有较好的适用性。
(2)与传统均匀设计响应面法相比,改进均匀设计响应面法建立的响应面模型精度有一定程度改善,最大增幅可达6.16%,能更好地对结构功能极限状态函数进行拟合;桥梁构件及系统在不同损伤状态下的损伤超越概率有所下降,最大下降幅度约为15.88%和18.69%;采用传统均匀设计响应面法进行易损性分析,可能会低估桥梁结构在地震作用下的抗震性能。
(3)与不考虑结构参数变量相关性相比,考虑变量相关性条件影响以后,建立的结构响应面模型精度有所改善,最大增幅约4.39%;桥梁构件及系统在不同损伤状态下的损伤超越概率均有一定程度的降低,最大降低幅度分别为12.90%和10.92%, 忽略结构参数变量相关性的影响,可能会高估桥梁结构在地震作用下的易损程度。

