基于多频简谐调制的风力机叶片裂纹检测研究

耿晓锋, 魏克湘, 王 琼, 杨博文, 吕 庆

(1.湖南工程学院 机械工程学院，湖南 湘潭 411104；2.风电运维与测试技术湖南省工程实验室，湖南 湘潭 411104)

风机叶片是重要的摄能部件[1]，其质量好坏直接影响发电效率。风力机叶片在实际运行中时刻受到循环载荷和空气中各种介质侵蚀[2]，表面容易产生微裂纹并由于应力集中裂纹逐渐扩张。风力机叶片是由多层玻璃布铺敷而成，每个单层都受到相邻层的约束力作用，裂纹会从表面扩展到深层[3]，最终导致叶片的失效。为避免由裂纹损伤引发的事故，研究含裂纹损伤风机叶片检测技术十分必要。

传统的线性检测技术受原理限制，对闭合裂纹的检测、复杂形状零件的检测、大型结构远端的检测、复合材料结构的检测等缺陷不可检或不敏感[4]。而当裂纹尺寸较小或为闭合裂纹时，基于振动与超声波调制的非线性效应无损检测技术比其他基于线性效应技术对裂纹更加敏感[5]。低频振动对高频超声波的调制作用，改变闭合裂纹交界面的接触状态，产生非线性耦合，可以很好地反映结构内部的裂纹、开裂等缺陷，不受材料和形状的限制。Klepka等[6]运用非线性调制方法成功识别了复合材料疲劳裂纹产生的非线性特征。Kim等[7]在匀速转动的风机叶片上，用振动声调制方法探测风力机叶片的疲劳裂纹。Parsons等[8]利用高频和低频激励对金属结构中的裂纹材料进行检测。Sohn等[9]利用非线性超声调制方法检测机翼与机身连接试件中的裂纹。胡海峰等[10]利用振动声调制方法检测板状金属结构中的裂纹。Dutata等[11]运用非线性声学方法对含裂纹构件进行检测，含裂纹的构件出现明显的声学非线性。廖泽平等[12]利用非线性振动声调制和同步锁相解调技术的方法检测悬臂梁中的疲劳裂纹。刘斌等[13]采用振动声调制技术对小径管座角焊缝进行检测，验证了该方法的可行性。从所参考的非线性相关的文献来看，大部分的研究工作主要是对非线性调制用于裂纹检测的定性分析很少有定量的评估。

本文以含裂纹的小型复合材料风机叶片为研究对象，采用多频简谐激励非线性调制检测方法，实验研究不同裂纹位置和长度下风力机叶片在多频简谐激励下的非线性动力学响应特性，定量评估裂纹特征对风机叶片的非线性调制影响，为风机叶片早期裂纹的检测提供参考。

1 多频简谐激励检测原理

多频简谐激励是基于非线性理论的一种思想，其调制现象的机理为：同时向被检测的结构中两个激励信号—高频超声波信号(fn)和低频振动信号(fm)，其中(fn>fm)，被检测结构会引起应变ε，应力为σ。应力应变关系可表示为：

σ=Kε

(1)

式中：K表示系统刚度。

向结构中施加激励信号引起应变ε可表示为

ε=Asin(2πfmt)+Bsin(2πfnt))

(2)

式中：A为低频信号振动振幅；B为高频超声波信号振幅；fm为低频振动频率；fn为高频超声波频率。

系统应力σ可表示为

σ=K(Asin(2πfmt)+Bsin(2πfnt))

(3)

当该结构无裂纹时为一个线性系统，即K为一个常数，从公式(3)中可知，该系统输出中只包含fm和fn两个频率分量，与输入信号频率相同，则系统不会出现非线性调制现象，如图1(a)所示。

当该结构存在裂纹损伤，系统刚度K为一个随应变ε变化的非线性函数K(ε)，则该系统为一个非线性系统。K(ε)用泰勒展开式表示为

K(ε)=α0+α1ε+α2ε2+α3ε3+…+αnεn

(4)

式中：α0为常数项，αi(i=1,2,…,n)为系统各阶非线性系数。

将非线性函数K(ε)代入式(3)，系统应力σ输出为

σ=ε·K(ε)=[Asin(2πfmt)+Bsin(2πfnt)]×
[α0+α1ε+α2ε2+…+αnεn]

(5)

由式(5)可知，由于结构中含裂纹损伤使得系统出现非线性调制。具体表现为，在输出σ信号中不仅包含fm和fn两个主频频率分量，还包括fn±nfm(n=1,2,3,…)的边频频率分量，如图1(b)所示。因此，在实际检测中，可通过分析检测信号中是否有边频频率分量的非线性特性，来确定结构中是否存在裂纹损伤。

图1 多频简谐激励非线性响应谱Fig.1 Nonlinear response spectrum of multi frequency harmonic excitation

2 多频简谐激励调制试验系统设计

以FD 2.8-1.0型1 kW风机叶片为研究对象，叶片长度为1 300 mm如图2所示。其中含裂纹损伤叶片包括：①距叶根390 mm处，裂纹长度分别为25 mm、35 mm、45 mm的风机叶片；②裂纹长度为25 mm，裂纹位置距叶根分别为390 mm、640 mm、890 mm处的风机叶片；在叶片表面加工一条宽为2 mm的V型槽，目的是加速裂纹扩展，模拟闭合裂纹，提高非线性调制敏感度。

图2 风力机叶片试样Fig.2 Wind turbine blade sample

多频简谐激励测试系统如图3所示，低频振动激励系统由F05型数字函数信号发生器、GF-20型功率放大器和JZ-2A型电磁激振器组成；高频超声波激励系统由F05型数字函数信号发生器、XE500系列压电陶瓷控制器和直径10 mm、厚度1 mm的圆形压电陶瓷片组成；信号采集系统由INVYJ9A型压电加速度传感器、DH5857-1电荷适调器和DH5922动态信号测试分析系统组成。激励系统中，激振器用弹性绳悬挂在支架上，顶杆固定位于距叶根350 mm处，产生低频振动激励；压电陶瓷片用胶水固定在距叶根360 mm处，产生高频超声激励；信号采集系统中的压电加速度传感器用强力胶粘贴至距叶尖100 mm处。

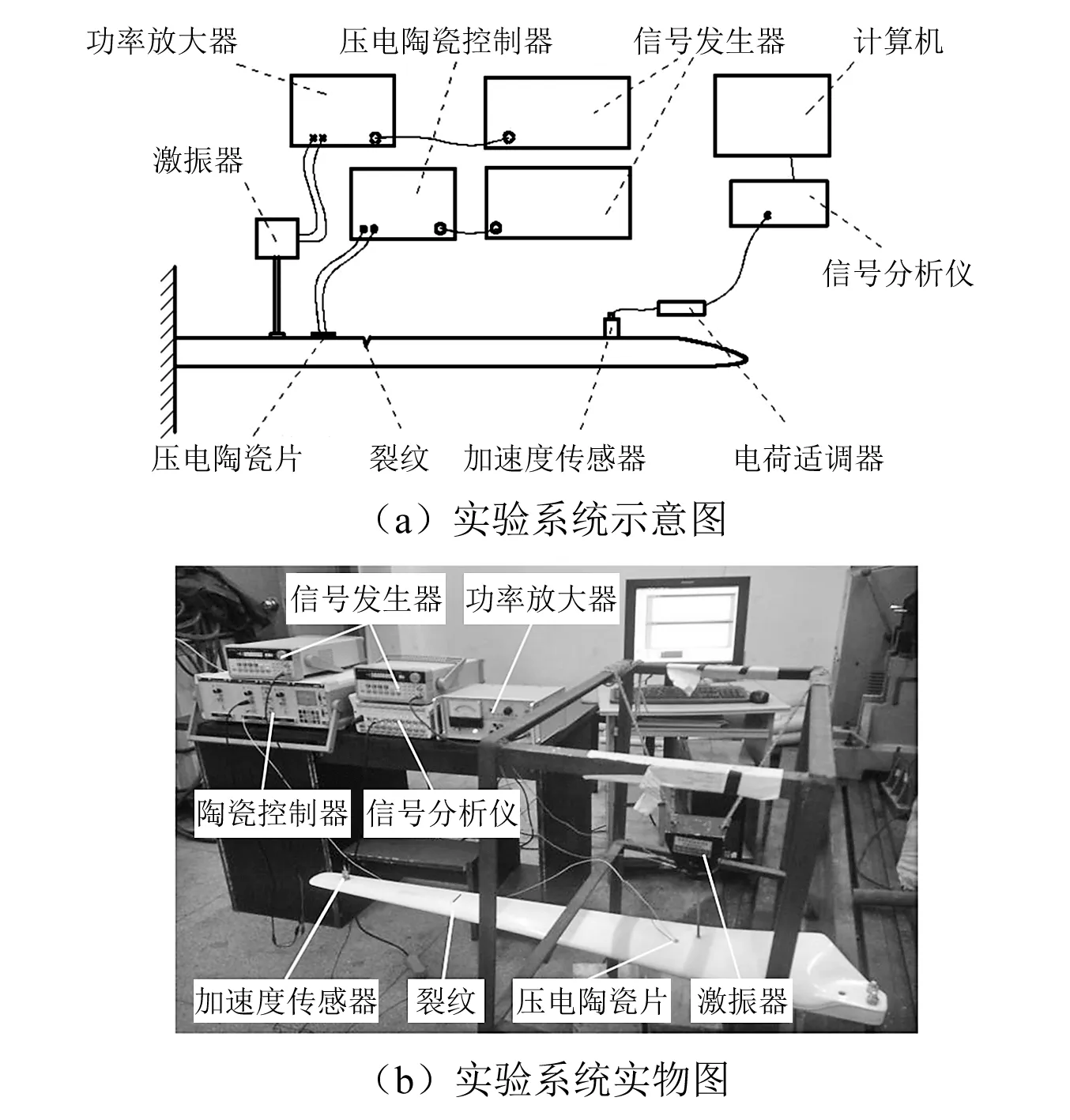
图3 多频简谐激励测试系统Fig.3 Multi frequency harmonic excitation test system

3 试验过程与结果分析

多频简谐激励调制技术中，振动特性参数影响调制现象的效果，当低频振动频率为风机叶片固有频率时，调制效果最明显。由于裂纹损伤长度和裂纹损伤位置改变，风机叶片的固有频率也会相应改变。经过测试观察分析叶片第4阶固有频率时的响应较其他阶次更强烈，故取第4阶固有频率作为低频激励频率。不同裂纹长度、裂纹位置下风机叶片第4阶固有频率如表1和表2所示。

表1 不同裂纹长度下叶片的固有频率

表2 不同裂纹位置下叶片的固有频率

经测试分析，当输入单一高频超声激励时，测得高频超声波信号频率为19 kHz、幅值11 V时风机叶片振动幅值最大，故本试验中高频超声波信号频率取19 kHz、幅值11 V。

根据上述多频简谐激励调制方法，测得含0 mm裂纹叶片和25 mm裂纹叶片的频谱图，如图4、图5所示。从图4和图5可以看出，含25 mm裂纹叶片的频谱图中低频频段和高频频段内有明显的调制现象，表现为叶片频谱图中19 kHz频段内出现明显调制边频带，且相邻边频之间频率间隔等于低频振动频率，在38 kHz频段内也可以观测到谱线；含0 mm裂纹叶片调制现象不明显。

图4 0 mm裂纹叶片非线性动力响应谱Fig.4 Nonlinear dynamic response spectrum of 0 mm cracked

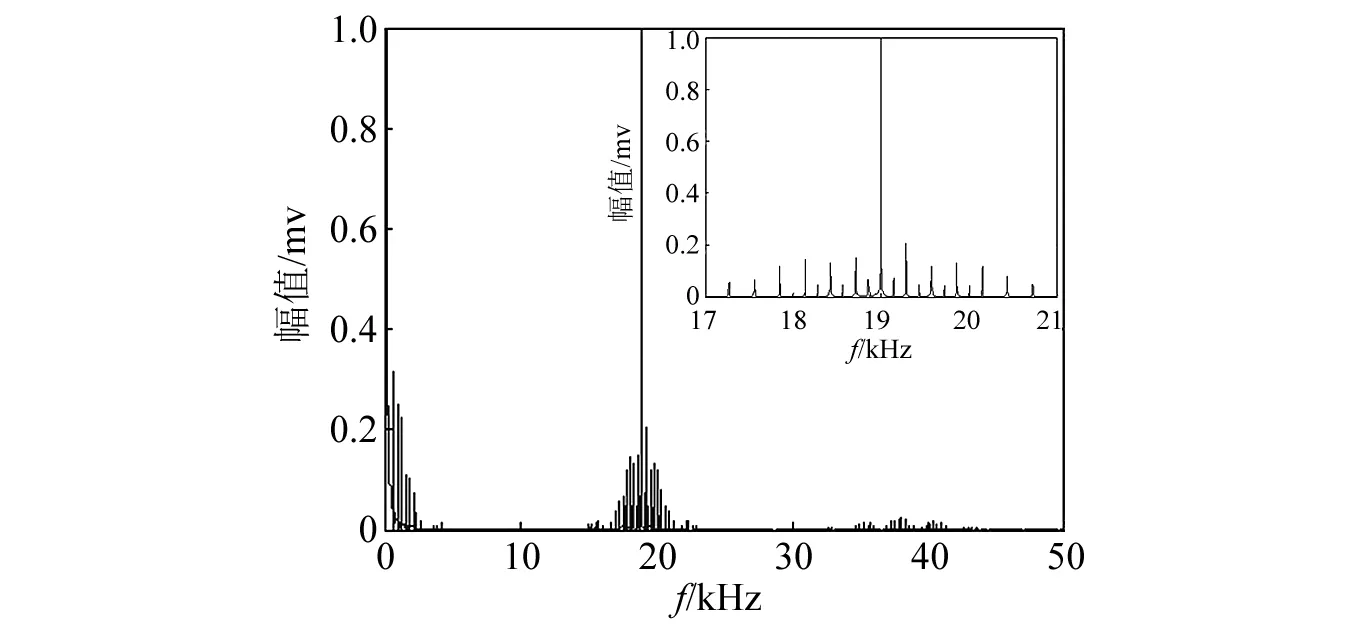
图5 25 mm裂纹叶片非线性动力响应谱Fig.5 Nonlinear dynamic response spectrum of 25 mm cracked

3.1 不同裂纹长度叶片的非线性动力响应特性

在距叶根390 mm处，分别对裂纹长度为25 mm、35 mm、45 mm的风机叶片进行检测，得到风机叶片非线性动力响应谱，如图6～图8所示。

由检测结果可知，裂纹长度为25 mm、35 mm和45 mm的叶片都出现了明显的调制现象。在其他参数条件都相同的情况下，不同裂纹长度损伤的叶片调制效果也有明显的差别。随着裂纹长度的增大，调制现象越来越明显，在低频段、19 kHz频段以及38 kHz频段内，边频数量和幅值都随裂纹长度的增大而增长。

为了更直观的分析裂纹长度为25 mm、35 mm、45 mm的叶片非线性调制变化的规律，比较非线性动力响应谱中19 kHz左、右前3个边频幅值，结果如图9所示。

图6 25 mm裂纹叶片非线性动力响应谱Fig.6 Nonlinear dynamic response spectrum of 25 mm cracked

图7 35 mm裂纹叶片非线性动力响应谱Fig.7 Nonlinear dynamic response spectrum of 35 mm cracked

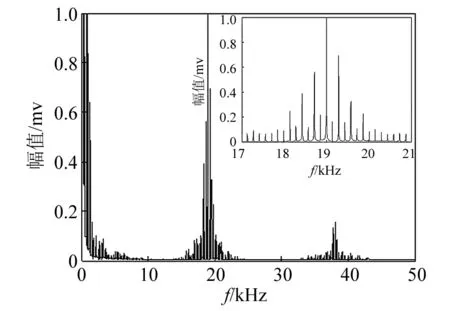
图8 45 mm裂纹叶片非线性动力响应谱Fig.8 Nonlinear dynamic response spectrum of 25 mm cracked

图9 19 kHz边频幅值变化规律Fig.9 Variation of amplitude of 19 khz side frequency

从图9中可以观察到裂纹长度为25 mm、35 mm、45 mm的叶片在19 kHz频段内的左右前3个边频幅值变化规律一致，幅值都随裂纹长度的增大而增大，非线性调制随裂纹长度的增加更强烈。

3.2 不同裂纹位置叶片的非线性动力响应特性

对裂纹长度为25 mm，裂纹位置距叶根分别为L1=390 mm、L2=640 mm、L3=890 mm的风机叶片进行检测，得到风机叶片非线性动力响应谱，如图10、图11和图12所示。

观察测试结果可知，裂纹长度为25 mm、裂纹位置分别为L1=390 mm、L2=640 mm、L3=890 mm处的叶片都出现了明显的调制现象。不同裂纹损伤位置的风机叶片调制效果也有明显的差别。随着裂纹位置到叶根的距离增大，调制现象越来越明显。在低频段、19 kHz频段以及38 kHz频段内，边频数量和幅值都随裂纹位置到叶根的距离增大，非线性调制越来越强烈。

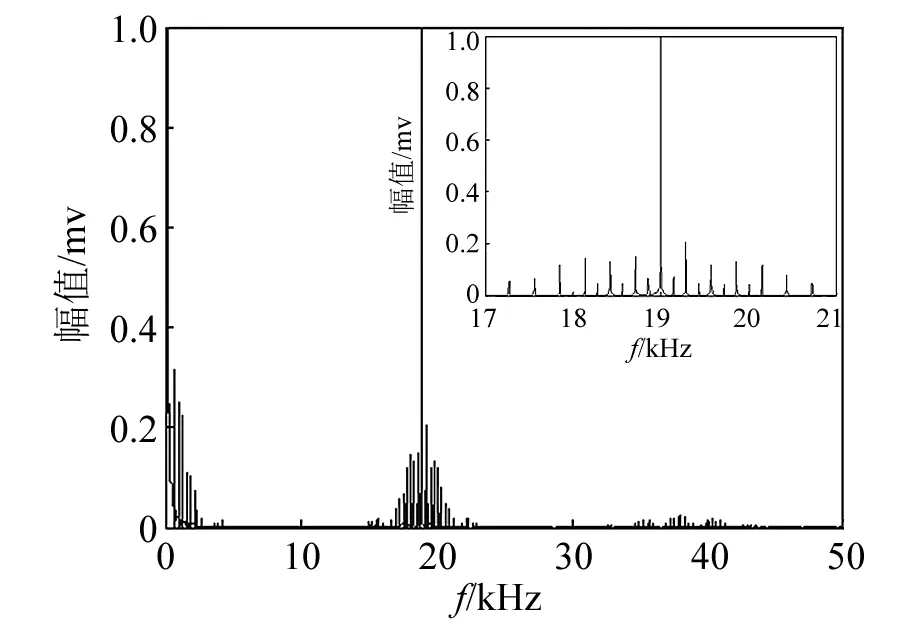
图10 390 mm位置裂纹叶片非线性动力响应谱Fig.10 Nonlinear dynamic response spectrum of blade in 390 mm position crack

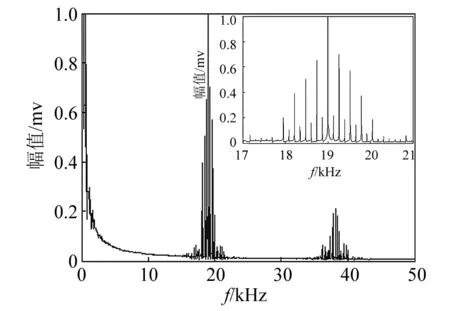
图11 640 mm位置裂纹叶片非线性动力响应谱Fig.11 Nonlinear dynamic response spectrum of blade in 640 mm position crack

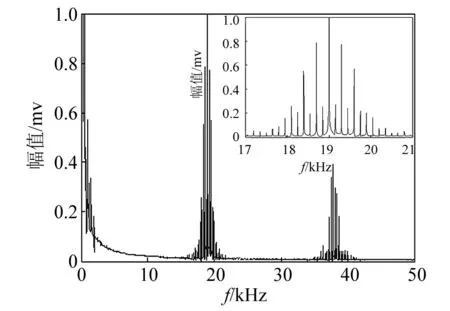
图12 890 mm位置裂纹叶片非线性动力响应谱Fig.12 Nonlinear dynamic response spectrumof blade in 890 mm position crack

提取非线性动力响应谱中19 kHz左、右前3个边频幅值数据比较分析，得到裂纹位置为L1=390 mm、L2=640 mm、L3=890 mm处风机叶片非线性调制变化规律，结果如图13所示。

从图13中可以观察到在19 kHz频段内的左右前3个边频幅值变化规律一致，边频幅值随裂纹位置远离叶根而增大增大。此外，当裂纹位置从L1到L2时幅值增长幅度较大，然而裂纹位置从L2到L3时，幅值增长幅度趋于平缓。

图13 19 kHz边频幅值变化规律Fig.13 Variation of amplitude of 19 khz side frequency

4 结 论

本文采用多频简谐激励调制方法对含裂纹损伤风机叶片非线性动力学特性进行研究。研究结果显示，在多频简谐激励调制下，含裂纹风机叶片出现了明显的非线性调制现象。其中，在同一位置下，随着裂纹长度的增加，风机叶片非线性调制现象越来越明显；同一裂纹长度下，随着裂纹位置到叶根的距离增加，非线性调制现象也越来越明显，其中19 kHz左右边频幅值和边频数量均增长，但其增长幅度趋于平缓。实验验证了该方法用于风力机叶片早期裂纹损伤检测的可行性。

作为一种新的无损检测方法，基于多频简谐非线性调制技术对风力机叶片中尺寸较小裂纹或闭合裂纹时仍然有许多问题需要解决，尤其是风力机叶片中其他缺陷如孔洞、脱胶等是否对检测的敏感度产生影响将是我们下一步要进行的工作。