浅谈数学思想在初中数学教学中的渗透

李 伟

(江苏省徐州市铜山区大许镇中心中学 221100)

新课程改革提出：“学生通过学习，能够获得适应未来社会生活和进一步发展所必需的重要数学知识以及基本的数学思想方法.”由此可见，培养学生的数学思想是我们今后的教学任务所在.数学思想是对数学教学方法、学习方法等的高度概括，是数学学习的精华，它是对数学的理性认识，是在数学问题的解决过程中提炼出来的，可以有效的帮助学生更快更好的理解数学知识.数学思想方法不是简单的文字体现，而是映射在数学知识中表现出来.教师在教学过程中要始终站在思想方法的高度，从培养学生观察能力入手，把数学思想渗透在教学过程的各个环节，切合落实数学思想的作用，不断提高学生的数学能力.接下来我们将对数学思想在初中数学教学活动的渗透策略进行详细介绍.

一、在初中数学教学中渗透转化思想，提高学生分析问题的能力

在初中数学的学习中，我们会遇到一些问题是常规方法难以解决的.这时候我们可以尝试转化为另一种思想看待问题，问题就可能迎刃而解.转化思想是数学思想的重要成员，它是指使一种对象在一定条件下转化为另一种研究对象的数学思想，在数学中体现为将原问题变化形态，使之转化为我们所了解的问题类型，可以帮助学生将复杂的问题简单化，转为我们熟悉的问题，加快解题效率.

如我们在学习一些较为复杂的方程组时,我们就可以利用转化思想，根据多个未知数之间的关系，把其他的未知数都用其中一个未知数表示，并把方程通分，这样不仅可以把方程化为简单的一元方程，还减少了计算量，大大提高解题效率，因此加强学生转化思想的培养刻不容缓.

如下题：

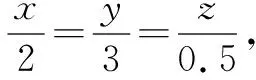
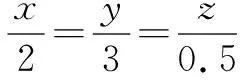
二、在解题练习中渗透数形结合思想，锻炼学生的数形转化能力

在初中数学中我们会遇到一些用数学关系难以解决的问题，需要学生利用几何图形来进行辅助解题，比如求函数的最小值等，如果我们直接计算难以找到答案，这时候适时采用数形结合思想，就可以把抽象的数量关系具体化，便于学生观察条件之间的关系，帮助解题更快更高效.数形结合不仅仅是重要数学思想之一，它还可以用来解决数学问题，它把许多数量关系的抽象概念和解析式用几何的方式表示出来，将问题具体化，还可以把图形通过数量关系的研究，变得更丰富、精确，是我们学生在数学学习过程中必不可少的数学思想之一.

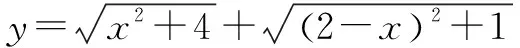
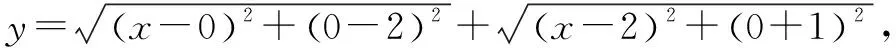
三、在课堂学习中渗透分类讨论方法，培养学生灵活处理问题的能力

分类思想是指让学生根据所研究对象的相同点和不同点进行区分，找出研究对象本质属性的共同点和差异点，在数学中尽量把问题的每一种情况类型列举清楚，找出数学对象之间的内在规律.分类是以比较为基础的，找出数学对象的不同并对之进行分类，更好地帮助学生总结归纳数学知识，使所学的知识条理化，有助于学生解题时思路更加清晰，解题目的更明确，帮助学生做题效率提高得更快.如下题就是一个很好的示范：

例3 当m是什么整数时，关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的根都是整数?

解因为是一元二次方程，所以二次项系数不为0，即m≠0，Δ1≥0，解得m≤1.

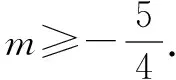
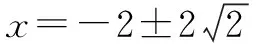
(2)当m=1时，方程1、2的根均为整数，所以m=1.

总的来说，数学思想是数学学习的关键所在，学生通过数学思想，可以摆脱过去数学带来的困扰，促进学生对抽象的数学知识的深层理解，将数学知识更好地掌握，帮助学生逐渐形成自己的学习方法，锻炼自主学习的能力，进一步提高学习能力.因此，我们教师要认真发挥数学思想对教学的促进作用，把数学思想有效地应用在教学的各个环节，引导学生认真地分析数学、理解数学，激发学生学习数学的积极性和热情，进而逐渐提高学生的数学学习能力，为初中数学教学质量的提高做贡献.