一种基于Turbo编码和离散小波变换参考子带的数字图像水印算法

李新宇

（湖南第一师范学院信息科学与工程学院，长沙 410205）

0 引言

在数字水印技术研究领域中，关于图像的水印技术已经有了很好的研究基础，同时由于其潜在的商业利益近年来一直备受关注，是数字水印技术领域中研究的热点。基于奇异值分解（Singular Vector Decompo⁃sition，SVD）的数字图像水印算法最早由Liu R和Tan T提出[1]，周波等人利用SVD的代数性质，对数字水印嵌入载体图像经SVD分解后的矩阵中，通过一系列的图像缩放、旋转、转置等几何攻击实验以后，发现提取出的数字水印具有良好的稳定性[2]。张秋余等人提出的算法首先对载体图像进行3层小波变换（Discrete Wavelet Transform，DWT），在中频子带上直接嵌入置乱后的水印信息并进行SVD分解，也取得了较好的实验效果[3]。

现有基于离散小波变换和奇异值分解的算法大多分为两类，第一类算法是将变换置乱后的水印图像的奇异值嵌入载体图像SVD分解后的奇异值中，提取水印时大多需要依赖置乱后的水印图像奇异值分解的正交矩阵，这样就降低了水印的真实性，容易造成虚警概率偏高的问题[4-5]。第二类算法是将水印经过相关变换置乱处理后直接嵌入载体图像SVD分解后的奇异值中，提取水印时一般需要原载体图像的奇异值矩阵。

张秋余等人提出的算法[3]是第二类算法的基础上同时又将置乱后的水印图像直接嵌入载体图像三级小波变换后的部分中频子带系数中，提取水印时还是需要置乱后的水印图像SVD分解后的U或V矩阵，不能有效地降低虚警率。钱华明等人提出了一种改进的基于SVD-DWT域的数字图像水印算法，将水印奇异值分解得到的正交矩阵U作为控制参数嵌入载体图像小波分解的细节子带中，再将水印的奇异值分别嵌入原始载体图像三层离散小波变换后低频子带的奇异值中，水印检测时将根据设置的极限值T检查提取的U'与原始U的相似性，只有相似性满足极限值T时才能进行水印的提取，算法克服了缺陷虚警概率偏高的缺陷，提高了水印信息的真实性，但是提取水印过程中需要原始载体图像的相关信息[6]。

熊祥光等人在文献[7]中详细论证了第一类算法虚警概率偏高的原因是在水印的提取过程中需用到水印图像SVD分解后的UW和VW矩阵，提出一种改进的混合DWT和SVD的图像水印算法。陈宏等人提出的算法[8]和文献[7]相似，对原始数字载体图像分块以后，根据每一个子块的纹理强度选取最佳水印嵌入子块，然后对最佳子块进行小波变换，同时对子块的低频系数进行奇异值分解，最后将置乱后的水印直接嵌入各载体图像子块的奇异值中。两种算法都有效的解决了虚警概率偏高的问题，提取水印时需要嵌入水印过程中生成的奇异值矩阵，从而无法实现水印信息盲提取。暴琳等人提出利用Tetrolet变换的优点和图像矩阵的奇异值稳定性好且代表图像内蕴特征的特点，提出了一种基于Tetrolet变换和SVD的图像盲检测稳健性数字水印算法，使水印系统具有良好的稳健性，但是该算法复杂度较强，运行时间较长,没有很好的实时性[9]。

1 算法描述

本文算法选择采用Logistic映射产生的混沌序列对Turbo编码后的水印图像进行预处理，生成加密后的编码水印W*，有效降低了误码率、提高了安全性。对原始载体图像I进行2×2大小分块，对每个分块SVD分解，取奇异值矩阵对角元素的第一个值组成矩阵Q，然后对矩阵Q进行8×8大小分块，并对其进行离散小波变换，选取小波分解后的低频子带LL2，对其再进行小波变换生成 3 个中高频子带（LH3、HL3、HH3），按照给定的阈值设置所选取的子带系数，随后进行小波逆变换形成参考子带LL’2并进行奇异值分解，取奇异值矩阵的第一个对角元素组成新的矩阵Q’，最后将Lo⁃gistic混沌置乱处理后的水印嵌入到新的矩阵Q’中。

1.1 水印嵌入

Step1原始彩色图像I的大小为M×N，对其进行RGB到YUV的空间转换，对Y分量2×2大小分块并进行奇异值分解，取分块奇异值矩阵对角元素的第一个值组成矩阵Q；

Step2然后对矩阵Q进行8×8大小分块，对每个分块进行二级DWT分解，然后选取DWT分解后第2层的低频子带LL2；其次对选取的子带LL2进行1层DWT变换，对生成的 3 个中高频子带（LH3、HL3、HH3），选取部分或所有的子带，并将所选取的子带系数的绝对值小于给定阈值的系数都设置为0，再进行1层DWT逆变换形成参考子带LL’2；

Step3最后对参考子带进行SVD分解，取奇异值矩阵的第一个对角元素，各个分块合成大小为的矩阵Q’，最后将Logistic混沌置乱处理后的水印嵌入到新的矩阵Q’中。

Step4水印图像W的大小为m×n，嵌入水印之前先计算量化值；

Step5将水印Wij的值嵌入奇异值矩阵的每一个值中；

Step6对嵌入水印以后生成的矩阵元素Qijw替换原来奇异值矩阵的第一个对角元素，然后对每一个新的奇异值矩阵进行反SVD分解，生成新的参考子带，对其进行二级逆向IDWT变换,然后将个8×8大小的分块合成大小为的矩阵，将每一个

矩阵元素代替Step1奇异值矩阵中的首个对角元素，随后进行反SVD分解得到2×2大小的矩阵，最后重构个2×2大小的矩阵合成嵌入水印的图像Iw。

1.2 水印的提取

水印提取算法如下：

Step1将可能遭受攻击的待检测图像I*w进行空间转换并进行2×2大小分块，对各分块进行奇异值分解，取分块奇异值矩阵对角元素的第一个值组成矩阵；

Step2对奇异值分解后的新矩阵按8×8大小进行分块，对每个分块进行二级DWT分解，然后选取DWT分解后第2层的低频子带LL2；最后对参考子带进行SVD分解，取奇异值矩阵的第一个对角元素Q*wij，进行水印的提取。

Step3根据嵌入水印时对水印图像计算出的量化值∂进行水印提取，得到提取出的水印值。

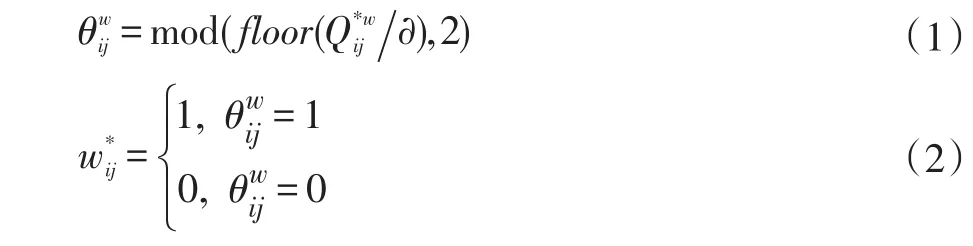
∂为量化步长，floor为截断取整函数，mod为求余函数。

2 实验与分析

本文算法的仿真实验操作系统平台为Windows 7，实验工具与软件平台为MATLAB 2012b，实验选取512×512 真彩色 Lena、Peppers、Baboon 作为载体图像，如图 1（a）、（b）、（c）所示，水印为 32×32 的二值图像如图 1（d）所示。

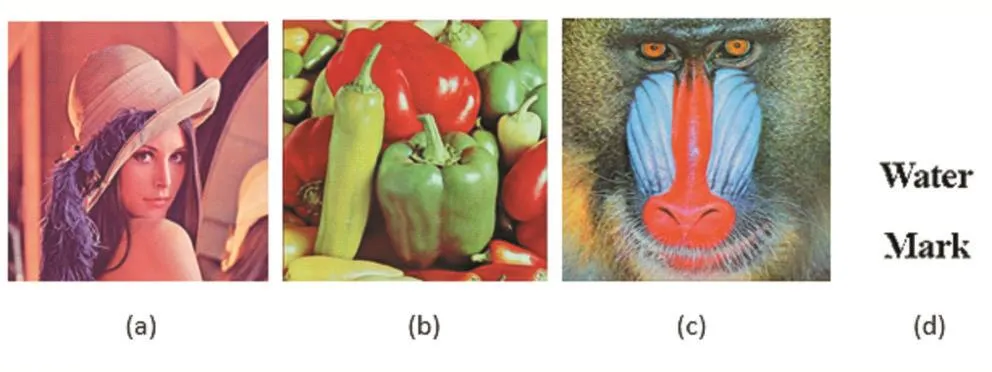
图1 Lena、Peppers、Baboon和水印图像

仿真实验中采用不同量化步长∂，嵌入水印后载体图像的PSNR值变化情况列于表1。

在实验中，图像的失真情况一般会采用峰值信噪比进行衡量，其值越大，说明图像失真越小，反之则失真越大。载体图像（a）、（b）、（c）嵌入水印后的图像峰值信噪比分别为42.8675、42.3108和42.6527，可见本文算法完全满足不可见性的要求。

为检验本文水印算法的鲁棒性，本文采用文献[10]提出的两极化相关值（Polarized Correlation，PC）来度量提取出的水印W^=（w^ij）和原始水印W=（wij）的相似程度，以此来评价算法所提取出水印的好坏效果，从而描绘出水印算法抗攻击的稳健性。PC值在0到1之间，越接近1就说明提取出来的水印和原水印越接近。在没有受到任何攻击的情况下，图像（a）、（b）、（c）提取出来的水印PC值均为1。二值图像水印的两极化相关值定义为：

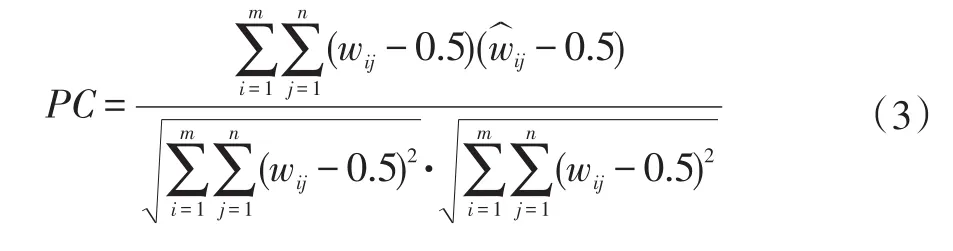
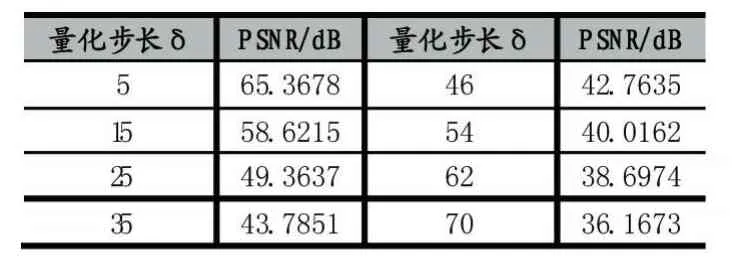
表1 不同量化步长下的PSNR值

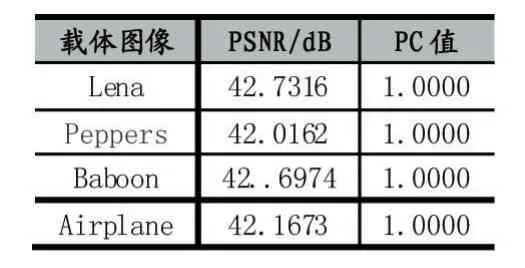
表2 不同载体图像嵌入水印的PSNR值和PC值

为了验证本文水印算法的性能，对含水印的Lena、Peppers、Baboon彩色图像分别进行如下实验：JPEG压缩、填加高斯噪声、中值滤波和剪切等攻击，仿真实验结果如表3所示。

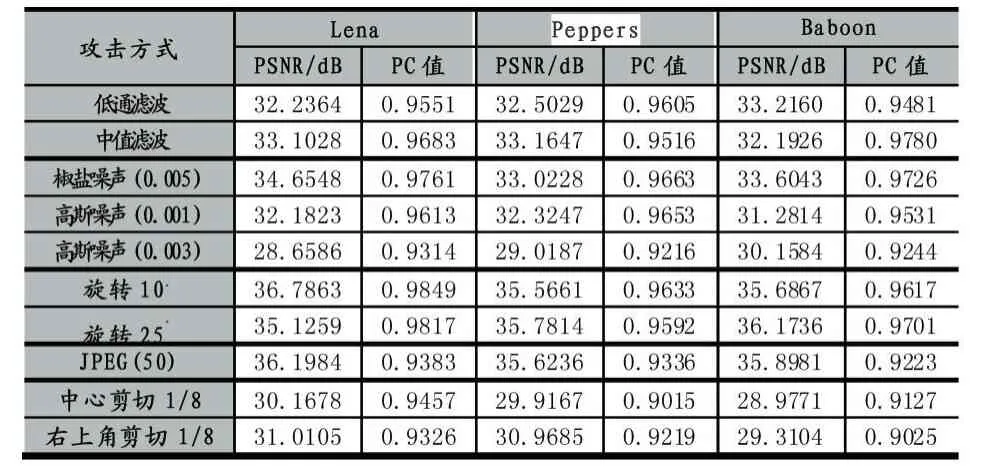
表3 仿真实验结果

为了验证本文算法的优越性，将本文算法（算法3）分别与 SVD_DWT（算法 1）和 DCT_SVD（算法 2）进行对比实验，对嵌入水印的载体图像进行滤波、噪声及几何攻击等处理。

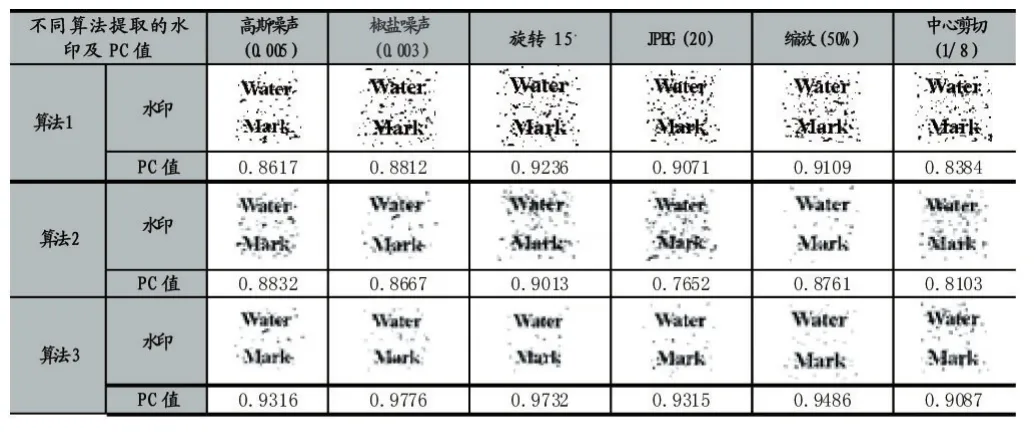
表4 类似算法对比实验结果

本文算法选择采用Logistic映射产生的混沌序列对Turbo编码后的水印图像进行预处理，然后采用量化最大奇异值的方法嵌入水印，而算法1采用替换SVD分解后前64个奇异值的最低有效位的方法，虽然能得到质量较高的含水印载体图像，但算法对噪声的鲁棒性较弱。算法2能有效降低时间复杂度，但是水印算法鲁棒性有待提高。为了便于比较，本文以Lena图像为例，恰当的设置各算法中的相应参数值，以保证两种算法在视频嵌入水印后图像的峰值信噪比PSNR相近，即水印透明性基本相同的情况下，再进行滤波、噪声处理、缩放和旋转等几个方面鲁棒性对比实验，相应的实验结果如表4所示。从实验结果可以看出，本文算法性能明显优于算法1和算法2。

3 结语

小波变换具有高低频分离的特点，提出了一种基于离散小波变换参考子带且结合Turbo纠错码的数字图像水印算法。首先对原始载体图像进行分块SVD分解，取对角元素的第一个值矩阵进行分块离散小波变换形成参考子带并进行奇异值分解，随后将预处理以后的水印信息嵌入到奇异值分解后的第一个对角元素矩阵中。本文算法结合DWT和Turbo纠错码的特性，再利用奇异值的特点，使其具备较强的鲁棒性和稳健性。通过对比实验发现本文算法尤其对高斯噪声、PSNR攻击、JPEG压缩、椒盐噪声等攻击具备鲁棒性，是一种高效、实用的数字图像水印算法。

本文利用了矩阵奇异值分解的能量稳定特性以及