向思维更深处漫溯
——浅谈小学数学的练习设计
江苏无锡市港下实验小学 杨 绘
仔细审视数学教材中的练习题,不仅有及时巩固新知,帮助内化的部分,适时地还穿插了一部分有很大提升空间的练习题,让学有余力的学生思考。而作为数学教师的我们,不仅可以通过练习获得学生学习的信息,而且可以有效利用好练习题,帮助学生思维发展与深化,现结合教学实例具体加以阐述。
一、举一反三——给思维“增温”
数学教材中的练习题,很多时候只是给我们提供了一些范例,如何从这些范例中找到相应的思维点,给学生更广阔的思维空间,这需要教师对知识进行“举一反三”的重组,从而让学生在步步紧逼的思维进程中感悟和收获。
【案例:苏教版数学三年级下册《长方形和正方形》】
在学习长方形和正方形的知识后,一般会安排如下的练习题,让学生体悟面积和周长之间的“变”与“不变”。

1.体会“等”与“不等”,让思维“保温”
生:这两块地的面积不相等,但是周长相等。
追问:你是怎样知道的呢?
生1:从图上可以看出一块地大,一块地小,所以面积不相等。
生2:我也从图上看到,萝卜地的周长是长方形的一条长加一条宽,再加中间一条曲线,白菜地的周长也是一条长和一条宽再加中间一条曲线。所以它们的周长相等。
一些学生听后点头表示同意,还有一些学生则有些茫然。
于是,教师把菜地图案抽象成下面的图形:
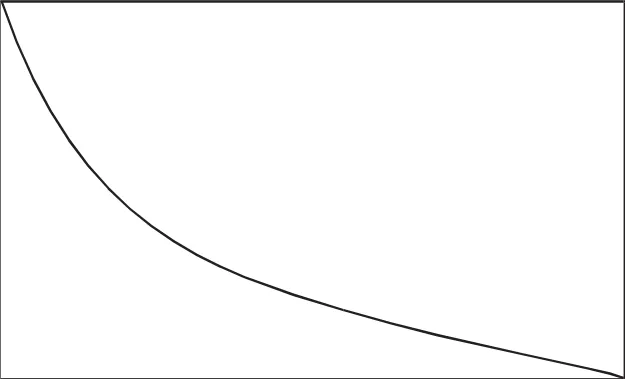
师:你能分别指一指萝卜地和白菜地的周长吗?
这道练习题通过比较长方形土地中两块菜地的周长和面积,让学生进一步深化对周长、面积意义的理解。练习中,大部分学生都能从图上直观地看出萝卜地的面积大一些。但是,对于两块地的周长的比较存在一些困难。让学生在直观图上指一指两块地的周长后,学生很自然地明确了两块地的周长相等。
2.体会“变”与“不变”,给思维“加温”
如果教学只单纯停留于上一阶段的学习,那么所获得的知识以及学生思维水平只是浅显和低层次的。为了拓展对周长、面积的认识,可继续往下走:
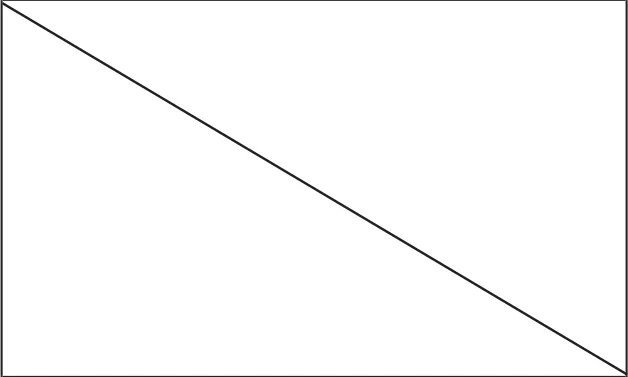
师:这种情况下,两块地的周长和面积又有什么关系?
生:两块地的周长相等,面积也相等。
师:你是怎样想的?
生:这两块地的面积都是长方形面积的一半,所以相等。它们的周长都是一条长和一条宽还有一条直线。
师:这两幅图有什么不同?
生:只是中间的那条线变了,其他都没发生改变。
师:是的,这条线起到了重要的作用,因为它的位置不同,引起了两块地面积的变化。但是两块地的周长都是长方形的一条长、一条宽和这条线,所以周长相等。
师:请你想一想,怎样画中间这条线段,就能让两块地的面积不相等,周长也不相等?
学生看着黑板上已有的两幅图陷入了思考……渐渐地有人举起了手。
师:大家可以在本子上试着画一画。
出示学生画的图:

师:请你来向大家介绍一下。
生:在这张图中,萝卜地的周长大。因为萝卜地从白菜地那里霸占了一小段过去。
大家都会意地笑了,“霸占”用得真好。
我继续追问:萝卜地霸占了哪一段呢?你能在图上指一指吗?
学生轻而易举地找出了被霸占的那一段,也就理解了为什么萝卜地的周长更长了。
对于一题多变的拓展练习,学生运用画图的策略展开了生动而深刻的数学思考,教师引导学生进行对比,分析习题中知识和方法中存在的内在联系,有效地提升学生的数学思考力。
充分利用教材中的练习题进行“举一反三”,让学生的思维不仅仅局限于基本习题,而且能从一题延伸到相关类型题目的解答方法,促使学生的思维不断深入,加深对所学知识的理解,培养良好的思维品质。
二、两种教法——给思维“设疑”
苏霍姆林斯基说过:“能够把少年‘拴’在你的思路上,引着他们通过一个个阶梯走向知识,这是教育技巧的一个重要特征。”练习课教学往往是对新知的延续和补充,对学生来说缺乏足够的吸引力。课堂上,教师如果能尝试不同教学方法,以此吸引学生的注意力,激活思维,相信一定会有不一样的收获。
【案例:苏教版数学五年级下册《分数的意义和性质》】
约分。

【片段一】

【片段二】
师:同学们已经会约分了,下面我们就来个三分钟约分比赛。

追问:观察一组分子和分母有什么特征,约分有什么技巧?
稍加思考后,学生们一下子了然了,积极表达的欲望高涨。
生1:分子和分母有倍数关系时,小的数就是他们的最大公因数,分子和分母同时除以最大公因数就可以约成最简分数。
生2:分子和分母都是11的倍数,直接用11来约分。
生3:分子和分母都是整十数,或是整百数,同时去掉相同个数的0,再约分。
生4:分子和分母没有这些特殊关系,在约分时我们可以逐一去找一找分子和分母有没有公因数2、3、5、7……应用以前学习的2、3、5的倍数的特征,可以提高我们约分的速度!
在片段一的教学时,只是简单地按照教材的呈现方式来展开教学,将所有的分数都混淆在一起,需要学生进行分类整理,再发现具有不同特征的分数在约分时的技巧,这对于绝大部分学生来说是相当困难的,所以课堂上教师提问后学生沉默了。在片段二的教学中,教师对分数进行了分类整理,列出了较为典型的具有同一特征的分数,学生从练习感悟—思索规律—恍然大悟,感受到了学习数学的乐趣。
只要教师善于寻找练习背后的精彩,有效展开教学,就能让学生既有的思维碰撞,又能品尝成功的喜悦,练习课同样鲜活、灵动、充满情趣。
三、适时改变——给思维“增色”
在练习课时,用足用好每一道练习题,明确每一道习题的作用和功能,显得尤为重要。教学中,教师还可对教材里的习题做适当调整、补充、拓展,让课堂走向开放,让学生的思维之花不断激发,知识不断深化。
【案例:苏教版数学五年级下册《简易方程》】
下表中的a、b、c表示3个连续的自然数。任意写出三组这样的数,并求出各组数的和。

a b c a+b+c
(1)观察上表,你有什么发现?在小组里交流。
(2)你会用含有b的式子表示a或c吗? 表示a、b、c的和呢?
(3)如果3个连续自然数的和是99,你能列方程求出这3个数各是多少吗?
这一练习有一定的难度,但这也是一个值得拓展的内容。如果运用得当,能激起学生的探究欲,寻找到规律所在,还能由此推导出其他相似的结论。在教学时,根据班级实际对练习进行拓展和重组。
师:观察上表,你有什么发现?在小组里交流。
在学生讨论的时候教师适当提示:这3个数与它们的和有什么关系?
有三个小组迅速得出了结论:3个连续的自然数,中间一个数乘3,就是它们的和。
其中有一位学生还精彩地举例论证了自己的结论:4、5、6,只要从6里拿出1给4,另两个数就变得和中间一个数一样大了,所以就可以用中间一个数乘3就行了。实际上她没有求和再除以3求平均数,而是通过移多补少来想的,更加简洁,易理解。经她这么一解释,再看看自己的例子,学生们一下子就明白了。有了移多补少的知识铺垫,学生只要想所举例子的几个数的大小关系就可以了。于是教师趁热打铁,马上问道:除了3个连续的自然数,还有哪些数也可能得出这样的结论?这一问,立即激发了学生的兴趣。他们猜测:
“4个连续的自然数,中间一个数乘4就是这4个数的和。”
“5个连续的自然数,中间一个数乘5就是这5个数的和。”
“3个连续的奇数,中间一个数乘3就是这3个数的和。”
“3个连续的偶数,中间一个数乘3就是这3个数的和。”
“3个连续的素数,中间一个数乘3就是这3个数的和。”
“3个连续的合数,中间一个数乘3就是这3个数的和。”
……
接下来,请四人小组任意选一个猜想举例论证。
小组成员有序、快速地活动起来。不久,教室安静下来,孩子们兴奋地举起了手,他们已经有满意的答案了:
生1:奇数个连续的自然数,中间的数乘个数等于它们的和。
生2:不一定非要连续的自然数,只要每相邻两个数的差相等就可以啦。
生3:奇数个连续的数,任意两个相邻数只要差相等,中间的一个数乘个数就等于它们的和。
多么令人惊喜的发现啊!他们由自然数联想到奇数、偶数,甚至联想到中学将要学习的等差数列,既有思维的广度,又有思维的深度。教育家皮亚杰说:“儿童是具有主动性的人,所教的东西,要能引起儿童的兴趣、符合他的需要,才能有效地促使他的发展。”数学教材是适合一般学生的学习内容,它不可能顾及每个学生的认知发展水平。事实上,由于受生活环境、学习条件等多种因素的影响,不同班级、同一班级不同学生的智力发展水平不尽相同。所以,教师可从学生的认知层面进行多方面的思考,对练习内容进行重组,让练习点燃每一个学生的智慧火花,满足每一个学生的求知欲。
数学课堂中的练习,如果只是对新知识的重复讲解、机械再做,学生会失去学习兴趣,思维能力无法得到提高。教师要从练习内容出发、从目标入手进行整体设计,积极调动学生的学习热情,引领学生的思维向更深处漫溯,让学生满载一船的收获,在数学世界里快乐放歌。♪

