椭圆中一类定点定向问题的充分必要条件①

王丙风

(江苏省南京市金陵中学 210005)

在文[1]中，通过平移坐标法的运用，给出了过圆锥曲线上一点作斜率乘积为定值的两条直线与圆锥曲线的另外两个交点连线过定点，文[2]发现了文[1]证明的疏忽，进而给出了更为严谨的结论，指出过圆锥曲线上一点作斜率乘积为定值的两条直线与圆锥曲线的另外两个交点连线过定点或定向．结论如下：

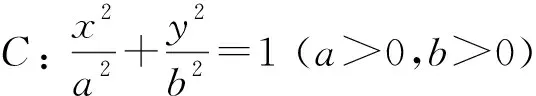
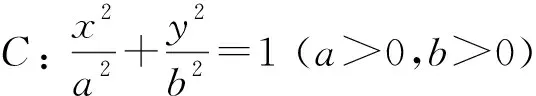
文[2]末指出，k1+k2为定值，可得出类似结论，经笔者计算，可得到如下结论：

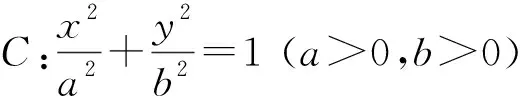
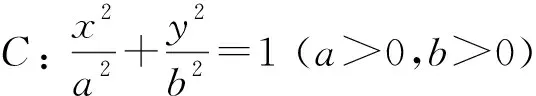
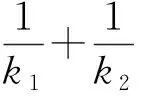
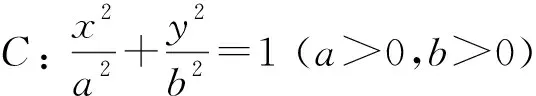
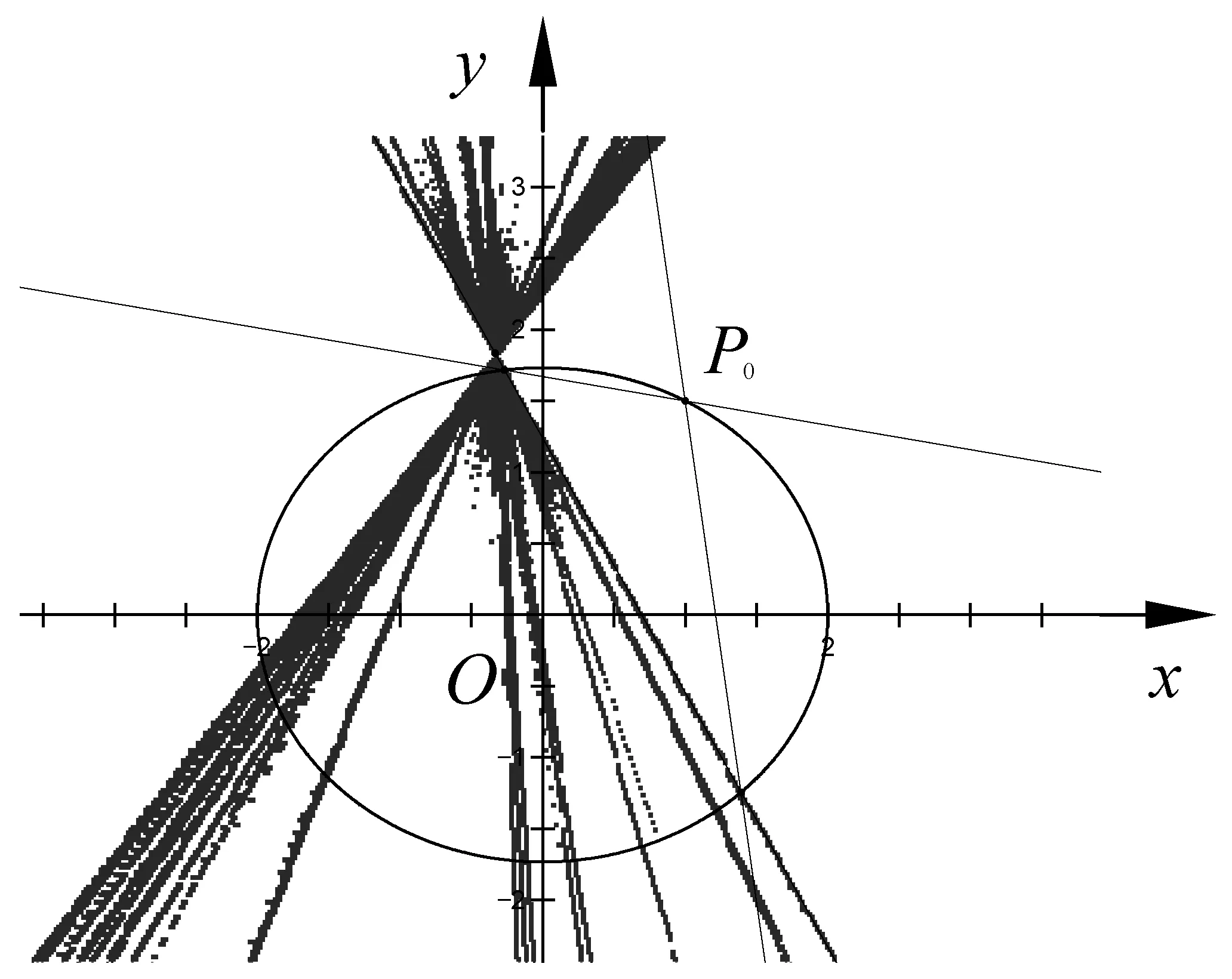
证明将坐标原点平移至P0点，

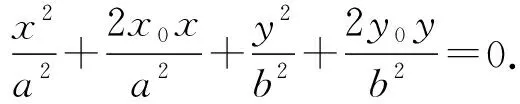
在新坐标系下若直线P1P2的斜率存在，

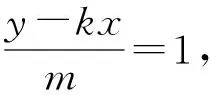
所以P1、P2满足

+b2(m-2x0k)=0，

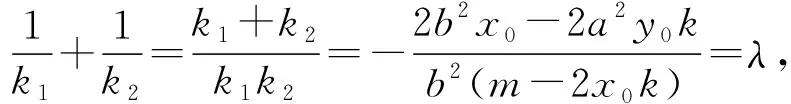
即2a2y0k-2b2x0=b2λ(m-2x0k)，

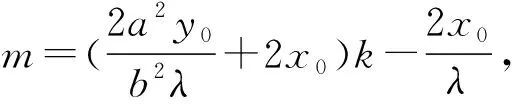
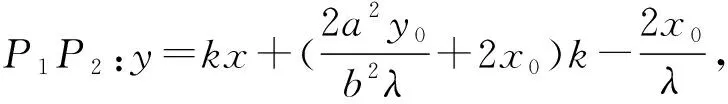
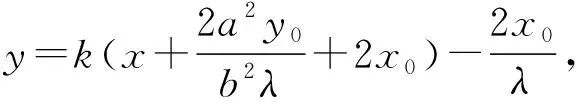
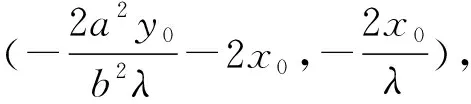
在新坐标系下若直线P1P2的斜率不存在，

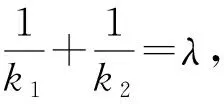
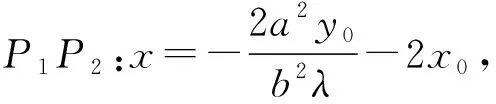
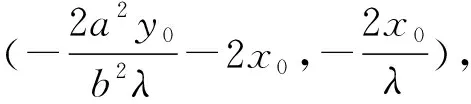
所以在原坐标系下直线P1P2过定点

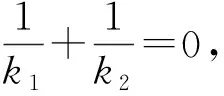
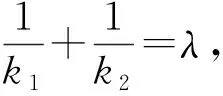
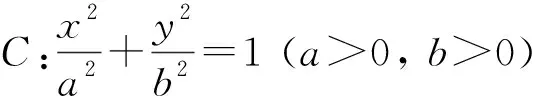
证明先证明充分性(存在不全为0的实数A，B，C使得Ak1k2+B(k1+k2)+C=0，则直线P1P2过定点或定向．)

若直线P1P2恒垂直于x轴，则P1P2定向；

若直线P1P2不恒垂直于x轴，

将坐标原点平移至P0点，

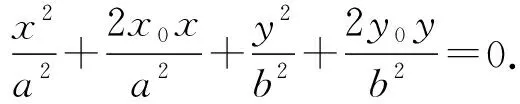
在新坐标系下若直线P1P2的斜率存在，

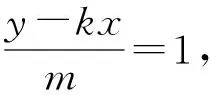
所以P1、P2满足

化简得

b2(m-2x0k)=0，

则Ak1k2+B(k1+k2)+C

=0，

(Ab2+Ca2)m=(2Ab2x0-2Ba2y0)k+

2Bb2x0-2Ca2y0，

若Ab2+Ca2≠0，则

则直线P1P2：

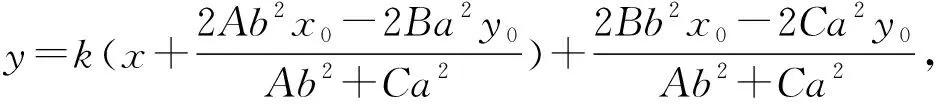
新坐标系下过定点

所以在原坐标系下过定点

若Ab2+Ca2=0，2Ab2x0-2Ba2y0≠0，则

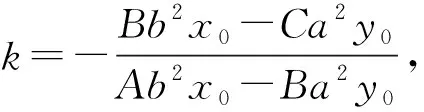
若Ab2+Ca2=0，2Ab2x0-2Ba2y0=0，

则2Bb2x0-2Ca2y0=0，

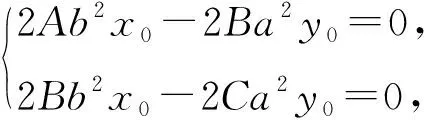
有非零解，则AC=B2，

若B≠0，则A、C同为正数或同为负数，

则Ab2+Ca2≠0，与Ab2+Ca2=0矛盾，不成立；

若B=0，则AC=0，Ab2+Ca2=0，

则A=0，C=0，与实数A，B，C不全为0矛盾，

不成立.

若直线P1P2的斜率不存在，在原坐标系下，

设P1(x，y)，P2(x，-y).

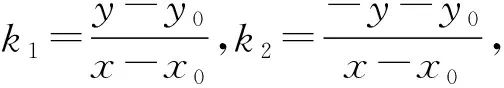
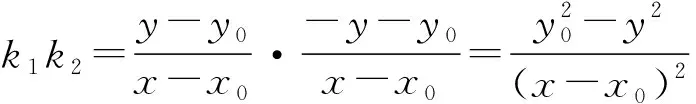
Ak1k2+B(k1+k2)+C

(Ab2+Ca2)x=(Ca2-Ab2)x0+2Ba2y0，

若Ab2+Ca2≠0，则

过定点

若Ab2+Ca2=0，则(Ca2-Ab2)x0+2Ba2y0=0，

即2Ab2x0-2Ba2y0=0，同上证明不成立.

充分性得证.

再证明必要性(直线P1P2过定点或定向，则存在不全为0的实数A，B，C使得Ak1k2+B(k1+k2)+C=0．)

若直线P1P2恒垂直于x轴，

设P1(x，y)，P2(x，-y)，

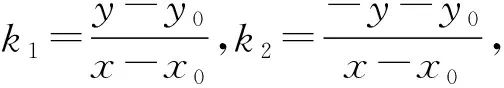
存在不全为0的实数A，B，C使得

Ak1k2+B(k1+k2)+C=0，

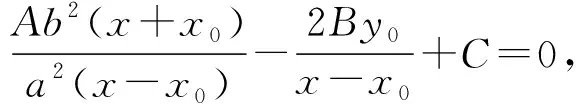
对x∈(-a，a)，x≠x0恒成立，

等价于

(Ab2+Ca2)x=(Ca2-Ab2)x0+2Ba2y0，

对x∈(-a，a)，x≠x0恒成立，

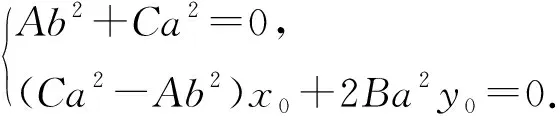
若y0=0，P为长轴端点，则k1+k2=0，

令A=0，B=1，C=0，

则Ak1k2+B(k1+k2)+C=0；

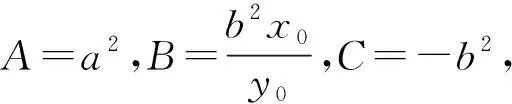
则Ak1k2+B(k1+k2)+C=0；

若直线P1P2不恒垂直于x轴，

将坐标原点平移至P0点，

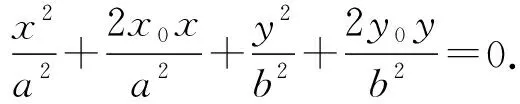
在新坐标系下若直线P1P2的斜率存在，

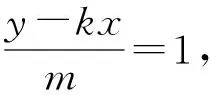
所以P1、P2满足

化简得

b2(m-2x0k)=0，

若P1P2定向，则k为常数，则

2b2x0-2a2y0k，b2(m-2x0k)为不全为0的常数，

则一定存在不全为0的实数A，B，C，使得

Ak1k2+B(k1+k2)+C=0.

若P1P2过定点，则m=uk+m0，

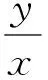
二次项系数为a2uk+a2(m0+2y0)，

一次项系数为-2a2y0k+2b2x0，

常数项系数为(u-2x0)b2k+b2m0.

若(a2u，a2(m0+2y0))与(-2a2y0，2b2x0)共线，又(a2u，a2(m0+2y0))≠0，(-2a2y0，2b2x0)≠0，

则根据共线向量定理，存在非零实数μ使得

μ(a2u，a2(m0+2y0))+(-2a2y0，2b2x0)

=0，

令A=0，B=1，C=-μ，

则Ak1k2+B(k1+k2)+C=0.

若(a2u，a2(m0+2y0))与(-2a2y0，2b2x0)不共线，

由平面向量基本定理，存在实数μ1，μ2使得

μ1(a2u，a2(m0+2y0))+μ2(-2a2y0，2b2x0)

+((u-2x0)b2，b2m0)=0，

令A=1，B=-μ2，C=μ1，

则Ak1k2+B(k1+k2)+C=0.

在新坐标系下若直线P1P2的斜率不存在，

则与y=kx+uk+m0过同一定点的直线P1P2：x=-u，

原坐标系下P1P2：x=-u+x0，

若(a2u，a2(m0+2y0))与(-2a2y0，2b2x0)共线，

同上令A=0，B=1，C=-μ，

Ak1k2+B(k1+k2)+C=0成立；

若(a2u，a2(m0+2y0))与(-2a2y0，2b2x0)不共线，

同上令A=1，B=-μ2，C=μ1，

则Ak1k2+B(k1+k2)+C=0.

必要性得证.

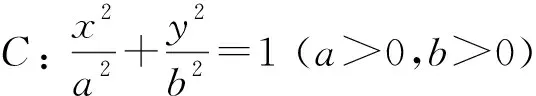
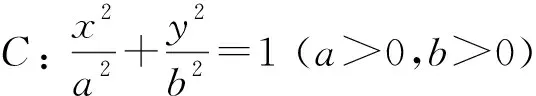
笔者研究发现，该定理推广到双曲线和抛物线中，也有相应的结论成立，这里不再赘述，感兴趣的读者不妨一试.

在数学解题的过程中，从条件到结论，只是我们数学解题的一部分，作为一名有着探究精神的研究人员，我们应该需要经常反问自己，要得到结论，需要哪些条件？条件与条件之间有关联吗？条件和结论之间有充分必要关系吗？只有这样，我们对知识的理解才会更为通透，更有利于知识体系的建立，我们对问题的探究才会更为深入，更有利于我们思维方式科学性和严谨性的建立.