递推：数列的灵魂①

李昌官

(浙江省台州市教育局教研室 318000)

递推是指按照一定的规律来计算序列中的每个项，其实质是把一个复杂的庞大的运算过程转化为简单过程的多次重复.

1 递推——代数学发展的根本大法

弗赖登塔尔认为：“数的概念的形成可以粗略地分成以下几种：计数的数、数量的数、度量的数和计算的数．”“无论从历史的、发生的还是从系统的角度来看，数的序列都是数学的基石．可以说，没有数的序列就没有数学．”[1]项武义认为，自然数系的本质就是一个顺序排列的体系，其起始者为1，往后顺序“后者”表示比“前者”多加1个，如此逐个加1以至于“无穷”；自然数系最原始根本的结构就是“+1”运算，加法是“+1”的复合，乘法是自相加的缩写，乘方是自相乘的缩写；自然数系的加、乘和乘方运算都是由最原始的“+1”运算逐步复合得到的．[2]这种逐步复合过程的实质是递推．加法结合律、乘法对加法的分配律、同底数幂乘法法则等都是通过归纳、递推得到的．有理数系运算、实数系运算、复数系运算是通过对自然数系运算的扩张、推广得到的．R·柯朗认为：“从n到n+1，这一步接一步的程序产生了数的无限序列，也构成了数学推理的一个最基本的类型(即数学归纳法)的基础”[3]．因此递推是代数学发展的根本大法．利用计算机运算速度快、适合做重复性操作的特点，可借助递推关系式编制计算机算法，让计算机对一组指令(或一定步骤)进行重复执行，因此递推是计算机算法的基础．

2 递推——数列的本质属性

大家都认可，数列是特殊的函数，是定义域为正整数集N*(或它的有限子集{1，2，…，n})的离散型函数．这个定义域有几个特点：一是它是离散的，是可列可数的；二是它是“均匀分布的”，相邻两个元素之间总是相差1；三是它有特定的起点1或n0．定义域“从特定的起点开始，连续均匀分布”是比离散更本质、更重要的特征．它决定了数列的项与项之间存在着某种内在的、确定的联系．而这种内在的、确定的联系决定了我们能用递推的方法解决数列问题．因此数列是用来刻画现实世界中一类具有递推规律事物的数学模型．递推是数列的本质属性，是数列与其他函数的最大区别．我们需要增强从递推视角思考和处理数列问题的意识．

3 递推——解决数列问题的根本大法

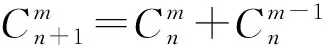
3.1 递推与等差、等比数列

部分教师认为等差、等比数列的通项公式是通过归纳得到的，可用不完全归纳的方法得到的结论怎能确保成立呢？如果是通过证明得到的，那又是怎样证明的？证明的方法又是什么？其实，合理而又紧扣问题本质的解决方法应该是归纳基础上的递推，应突出和强化递推在公式推导过程中的核心价值．应认识到用归纳猜想的方法得到结论与用递推论证的方法确认结论是两种不同水平的思维；前者是经验化、表面化的，而后者则准确地把握了问题与方法的本质，它蕴含着数学归纳法的基础与萌芽．以等差数列通项公式的推导为例，由a2-a1=d，有a2=a1+d．由a3-a2=d，有a3=a2+d=a1+2d，…由an-an-1=d，这个过程可以无限地递推下去．

3.2 递推与数学归纳法

“对于自然数系本质的朴素的描述就是数学归纳法原理”[2]．尽管数学归纳法有第一数学归纳法、第二数学归纳法、跳跃归纳法、递降归纳法、倒推归纳法、螺旋归纳法等各种形式，但其本质与核心都是递推．递推使数学归纳法跨越了“有穷”到“无穷”的障碍，得到一个对不小于n0的任何整数都成立的数学命题．利用数学归纳法证明的核心与关键是由“n=k”时命题成立推出“n=k+1”时命题也成立．因此数学归纳法既源于递推思想，又应用递推方法．

3.3 递推与叠加、叠乘

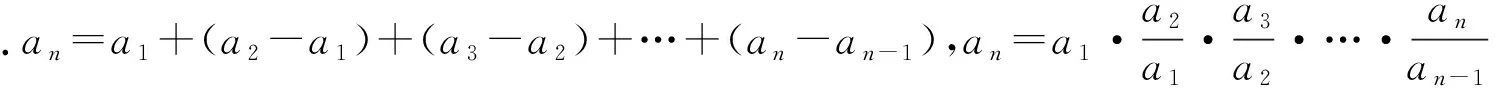
4 运用递推解决数列问题的步骤

运用递推解决数列问题通常有如下四个步骤：

第一步，明确递推的起点．递推总是在一定的基础上进行；离开递推的起点，递推就无从谈起．因此明确递推起点是解决数列问题的前提和基础．

第二步，建立递推关系式．事物发展总有前因后果，搞清楚事物发展的前因后果及其相互联系，搞清楚事物的形成过程与形成方法，是寻找解题思路、突破思维难点的有效方法．用递推的观点看待问题，搞清楚前后项之间的关系，建立递推关系式，这是解决数列问题的核心环节．

第三步，对递推关系式进行变形．递推的本质是拓展与推广，而拓展与推广就需要紧紧抓住事物的共同点与本质．由于事物的本质与规律往往隐藏在各种现象的背后，发现难度大，因此通过递推关系式的变形发现规律往往是解决数列问题的难点．

第四步，求出结果．在通过递推关系式变形把陌生问题转化为熟悉问题、把未解决的问题转化为已解决的问题后，求出所要求的结果．

下面通过两个案例说明递推思想与方法在解决数列问题中的运用．

分析由题设可知，数列{Pn}的后一项是由前两项按一定的规则得到的，因此可用递推的思想与方法解决．

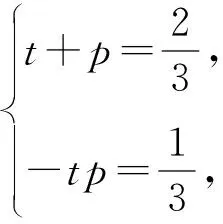
因此有

或

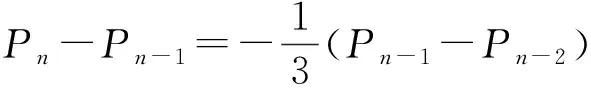
案例二n对夫妻跳舞, 要求每人都有舞伴且夫妻不许伴舞, 有多少种伴舞方案?

分析此问题条件简单，直接求符合条件的n对夫妻舞伴的方案总数an难度很大．尽管表面上看数列{an}项与项之间的递推关系不明显，但如果不搞清楚其递推关系，就无法清楚其变化与发展的规律，也就无法求出an．

第一步，明确递推的起点．将n对夫妻编为1,…，n号,设符合要求的n对夫妻伴舞的方案总数an,易知a1=0，a2=1．

第二步，寻找递推关系式．考虑在n对夫妻的基础上增加第(n+1)对夫妻带来的伴舞方案数的变化．第(n+1)号男士的舞伴有n种可能．不妨设他选中了k号女士．对k号男士，如果他选中了(n+1)号女士，则其他(n-1)对夫妻安排伴舞的方案数为an-1；若他选中了其他女士，可将(n+1)号女士的编号改为k号, 从而问题就转变为安排n对夫妻伴舞, 其方案数为an．因此有

an+1=n(an-1+an)(n≥2)．

①

第三步，对递推关系式进行变形．由①，瞄准构造新的等差数列或等比数列的目标，利用观察法或待定系数法，可得

an+1-(n+1)an=-(an-nan-1)，

an+1-(n+1)an=(-1)n-1，

②

第四步，求出结果．由②，有

……

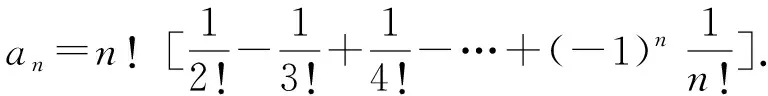
5 运用递推关系式的策略与方法

许多数列问题已经给出递推关系式，此时对递推关系式进行恰当的变形往往既是问题解决的核心与关键，也是问题解决的难点之所在．

5.1 明确变形的目标与方向

递推关系式变形的目的是为了更好地揭示关系式所蕴含的数学规律，是为了更好地实现由数列首项到末项的递推．就中学数列问题而言，为了有效地解决问题，通常要构造出一个新的数列．这个新的数列应是等差数列或等比数列，或可以利用叠加、叠乘法求解的数列，或其他能由首项逐步递推到末项的数列．

5.2 明确变形的常用思路与方法

5.2.1 “凑”

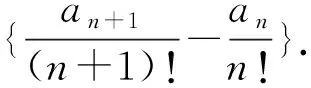
5.2.2 待定系数法

在把握待构造的新数列特点的基础上，先猜想含有待定系数的新数列，再根据相关条件求解这些系数．如案例一的第三步，先设Pn-tPn-1=p(Pn-1-tPn-2)，然后再求出t与p的值．

5.2.3 借助不动点

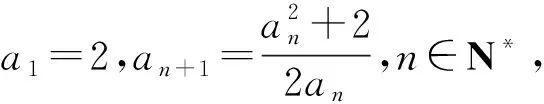
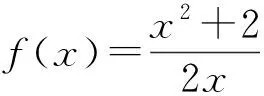
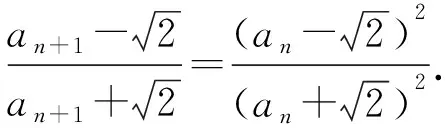
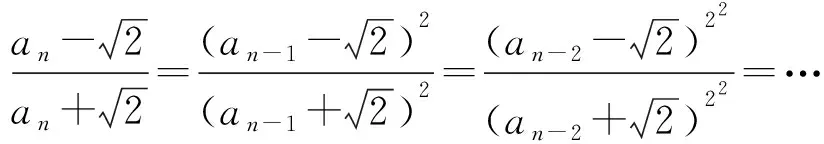
5.3 建构新的递推关系式

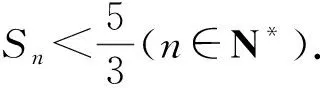
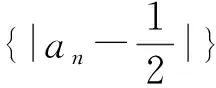
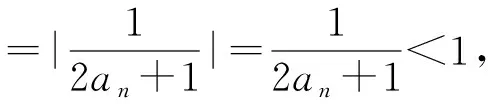
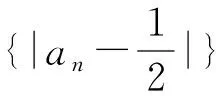
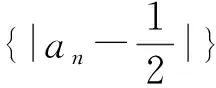
递推是数列的灵魂，是解决数列问题最重要、最根本的思路与方法．从更高层次看，递推属于递归，其实质是“运用已经收集到的信息作为行动的基础去收集更多的信息”[4]．