单叉剪式升降台结构相关参数计算公式的确定
宫敏利
(湖南财经工业职业技术学院机械工程系, 湖南 衡阳 421001)
引言
剪式升降台具有剪叉机械结构,作业平台宽大,承载能力高,载物台在起升过程中有较高的稳定性,广泛用于搬运、装卸等物流作业现场,在有高度落差设备之间实现物料上下线、仓储上下料[1]。
图1所示单叉剪式升降台的实物结构,是最常见的固定式底座的剪式升降台。该升降台主要由载物台(台面)、剪叉机构、驱动元件、底座以及铰连件等组成,其中驱动元件可选用液压油缸或螺杆机构等,铰连件可选用销套、关节轴承等。
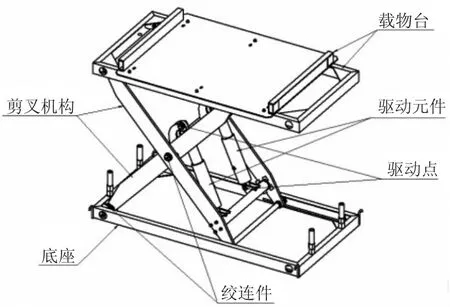
图1 单叉剪式升降台实物结构图
在升降台结构设计中,驱动元件与剪叉机构的铰连点常常称为驱动点,其位置选取是设计的关键环节,它影响着升降台在最低位置工作时的举升力大小,从而决定了升降台工作性能的优劣[2]。目前,大多设计者通过三维设计软件根据结构空间范围主观确定出大致尺寸和形状,但往往确定的结果并不是最佳状况,可能在制造或使用时需多次修正[3]。因此,本文从升降台的结构入手,根据尺寸的关联关系推导出对应的结构尺寸计算公式,同时根据力学理论得出驱动力的计算公式。
1 结构尺寸计算公式推导
1.1 结构模型及结构参数
为了便于分析和推导,构造出升降台的简易结构模型,如图2所示。

图2 单叉剪式升降台简易结构模型
根据单叉剪式升降台的使用情况和设计分析需求,提取下页图3所示的结构参数,其中J0—J4均为铰连点、Ja和Jb为驱动点。按照参数类型的不同,分为如下四种:
1)运行变量:主要有台面高 Hhi、铰垂距 Hi、驱动元件(油缸)长度Ui和剪叉夹角θi,具体数值取决于不同工作位置状态。
2)设计给定量:主要有台面长度T、驱动元件(油缸)长度Ui的最大值Umax与最小值Umin、台面高Hhi的最大值Hhmax与最小值Hhmin,其数值通常由使用者根据自身工况需求条件来确定。
3)设计设定量:主要有铰边距t和铰台距h1、h2,其数值由设计者根据使用经验来选取。
4)设计计算量:主要有剪叉长L、上驱动点距A及其点距角α和下驱动点距B及其点距角β,这些数值可通过分析推导计算得到。
在使用过程中,关注升降台的两种极限位置状态:一是载物台处于最低位置状态,此时台面高Hhi=Hhmin、油缸长度Ui=Umin;二是载物台处于最高位置状态,此时台面高Hhi=Hhmax、油缸长度Ui=Umax。
1.2 台面处于最低位置状态
下页图4给出了载物台处于最低位置时的状态,即升降台回位或收起的状态。此时,台面高Hhi=Hhmin、油缸长度Ui=Umin,台面长度T为给定数值。
设定铰边距t1=t、铰台距h1=h2,则:铰平距铰垂距 Hi=Hhmin-2h1=Hmin,剪叉长 L=,剪叉夹角

图3 单叉剪式升降台的结构参数

图4 载物台处于最低位置的状态
当载物台处于最低位置时,驱动点Ja、Jb的设置应为:上驱动点Ja放置在J1、J2连线上,得到J1Ja线段,即驱动点距A;下驱动点Jb放在J3、J4连线上,得到J4Jb线段,即驱动点距B。只有这种设置才能使油缸在最小空间高度内处于仰角最大,不仅与台面、底座不发生干涉,且油缸所需的举升力最小,故此为最佳方案。
当Umin≥Hmin时,驱动点距A、B的水平投影差为。而当 Umin<Hmin时,油缸需进行接长以满足结构尺寸的需求。
1.3 台面处于最高位置状态
同理,图5给出了载物台处于最高位置时的状态,即升降台满行程升起工作的状态。此时,台面高Hhi=Hhmax、油缸长度 Ui=Umax。
铰垂距 Hi=Hhmax-2h1=Hmax,剪叉夹角 θi=θmax=2sin-1。
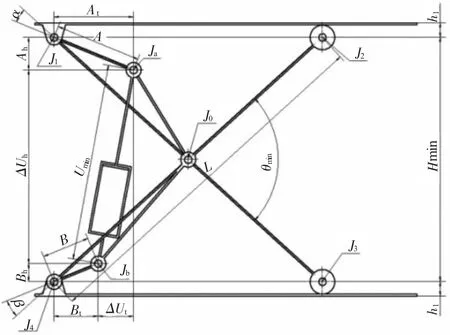
图5 载物台处于最高位置的状态
由三角形勾股定理可知,油缸最大长度Umax满足关系,由此可得,油缸垂直投影即 Hmax-。整理式子得到:A+B=
2 驱动力计算公式
2.1 驱动力臂计算
图6为载物台处于任意高度时的状态,此时铰垂距Hi、剪叉夹角θi和驱动元件(油缸)长度Ui为运行变量。
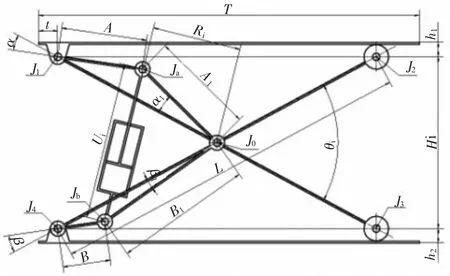
图6 载物台处于任意高度位置的状态
由三角形的余弦定理可得,上驱动距A1=, 下 驱 动 距 B1=
由三角形的正弦定理可得,上驱动角α1=sin-1,下驱动角
2.2 驱动力计算
当载物台承重时,重物压力载荷通过铰连件传给剪叉机构,再由剪叉机构传到底座。为了分析方便,先不予考虑升降台自重[4],又因剪叉机构左右两边对称,故取其中一个剪臂进行受力分析,剪臂受力如图7所示。
设载重物的重量为P。由力学知识可知,P1=P2=

图7 升降台剪臂受力图
当以J0为转动支点,则有剪臂合力矩ΣM=0,即而铰平距,由此可得:驱动力
根据以上结构尺寸计算公式的推导结果和驱动力的计算公式,利用VisualBasic软件可以快速求解出升降台的结构尺寸参数,本文不作详细说明。
3 结语
本文所述的单叉剪式升降台结构尺寸参数确定的计算公式,已被成功地应用到胶合板锯边、磨光生产线的多规格升降台快速设计中,相比原有设计方法大大缩短了产品的设计开发周期。同时,该方法实现了用一种规格油缸设计出多种升程的升降台,制造出的升降台实际升程与设计升程误差率小于0.5%,剪臂受力减少10%~20%。

