一种基于补偿的多水下升降台精确定位方法
胡丹丹,王力,牛国臣
(中国民航大学机器人研究所,天津 300300)
0 前言
升降舞台是现代演艺中常用的一种舞台表现形式,一般应用于剧院等场所,根据设计的舞台效果进行升降台的编组运行,通常要求升降台具有较高的位置控制精度[1-2]。近年来,为满足演出需求,将升降舞台应用于水中,如镇江大型水景秀《白蛇传》具有40块水中升降舞台,每块可以独立升降。
升降台通常采用电动、液压等驱动方式,由于升降台位于水下,采用液压方式存在液压油渗漏污染水质的问题,因此,采用电动方式。在升降台同步控制方面,基于模糊控制[3-4]、模糊神经网络[5]、耦合策略[6-9]等对异步电机同步运行的研究很多,但对升降台同步运行影响最大的因素是机械传动误差。系统中使用钢丝绳进行远程传动,但钢丝绳具有弹性,当受力变化时弹性伸长不同,存在升降台换向迟滞现象,控制精度下降。
当系统整体为线性,而局部呈现非线性时,通常采用补偿等方式以减小非线性因素对控制性能的影响。针对上述问题,拟设计一种基于补偿的位置控制方法,以提高升降台的位置控制精度。
1 水下升降台系统构成
图1为单台升降台的示意图。
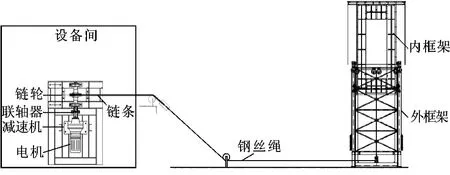
图1 水中升降台示意图
由于升降台位于水下,为减少驱动装置对水质影响,采用电机驱动方式,电机等驱动装置位于岸边的设备间中。传动装置主要为减速机、联轴器、链轮、链条和钢丝绳,通过钢丝绳远程牵引升降台运行。为节约空间,使用链轮链条传动方式代替卷筒对钢丝绳进行收放。升降台为框架式结构,主要由内框架和外框架组成,外框架固定在地基上,内框架嵌套在外框架中,设计动滑轮和定滑轮,内框架通过钢丝绳牵引沿着外框架的导轨进行升降运动,构成一级动滑轮。
2 升降台位置控制
常见的升降台控制方式有两种,一种是“上位机+服务器+轴控制器+驱动单元”的方式,另一种是“上位机+可编程控制器(PLC)+驱动单元”的方式[10-11]。第一种方式需要专门的轴控制器,成本很高且不易后期维护,第二种方式可根据系统需求灵活选型,且可靠性高,应用较为广泛。因此,该系统设计中选择以PLC为核心的控制方式。
升降台控制系统以工业上应用广泛且性能稳定的工控机、PLC作为核心控制器,矢量型变频器作为驱动装置,电机选择适用于频繁变频调速的变频电机,采用“PLC+矢量型变频器+变频电机+编码器”控制方式对电机进行伺服控制。
为实现升降台的位置伺服控制,一般是在升降台侧安装编码器反馈升降台的实际位置信息形成闭环。由于升降台位于水面下,若在其上安装编码器,需要在水中工作,且升降台距离控制端最远可达上百米,编码器信号衰减很大。因此,在升降台上安装编码器很难达到理想的效果。故采用在电机尾轴上安装编码器方式,构成电机位置闭环负反馈系统。对变频电机进行精确的位置控制,经过传动装置进而控制升降台的位置,升降台位置控制结构如图2所示。

图2 升降台控制结构图
PLC通过发送高速脉冲信号控制变频器,变频器驱动电机,进而控制升降台运行。脉冲信号频率决定运行速度,脉冲信号个数决定电机运行位置,且脉冲个数与位置为正比例关系。
3 升降台运行误差分析
3.1 零位误差
对升降台进行位置控制,需要明确定位的基准位置,称为位置零点。一般是设置机械限位开关,以升降台向下运行触碰限位开关的位置作为机械零点。但当升降台的数量较多时,为保证台面平整需逐一调整限位开关,工作量很大。由于限位开关位置差异造成的定位误差称为零位误差。
3.2 换向误差
对于上述工作方式的升降台位置控制时面临因传动误差影响造成难以准确定位的问题。下面对升降台运行中受力情况及传动误差产生的原因进行分析。
升降台运行时主要受钢丝绳拉力、运行阻力、自身重力,对其进行受力分析,上升和下降时受力情况不同,如图3所示。其中,图(a)为升降台上升时受力情况,图(b)为升降台下降时受力情况。由于阻力始终与运行方向相反,因此,上升时阻力方向向下,下降时阻力方向向上,匀速运行时钢丝绳拉力与运行阻力和升降台重力关系如式(1)。
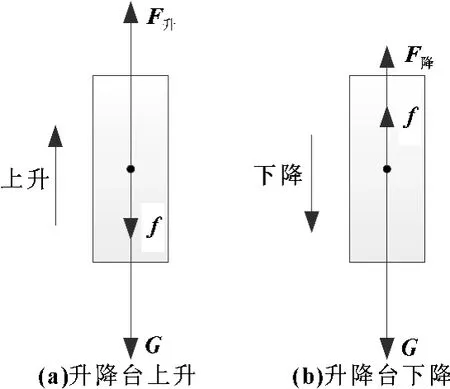
图3 升降台受力分析

式中:F升为上升时钢丝绳拉力,F降为下降时钢丝绳拉力,G为升降台内框架重力,f为运行阻力。
钢丝绳中拉力变化:
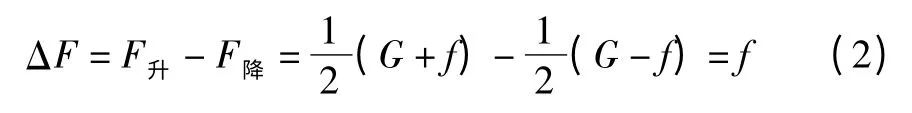
式中:ΔF为升降台上升和下降时钢丝绳中拉力变化。
由式(2)可知,由于升降台运行阻力的影响导致钢丝绳中拉力在上升和下降时发生变化。
钢丝绳在拉力作用下的伸长量可由式(3)计算,对于同一个升降台,钢丝绳伸长量与施加的载荷成正比,可以得到钢丝绳的伸长变化量ΔS与载荷变化量Δm成正比,即式(4)所示。升降台匀速运行时,施加载荷所产生的力与钢丝绳的拉力相等。因此,由式(1)可知升降台在上升和下降过程中钢丝绳受力不同,受力变化由运行阻力造成,变化量如式(2)所示。在升降台运行方向改变时,由于钢丝绳受力变化导致其伸长变化而产生误差,称为换向误差。

式中:S为钢丝绳伸长量,ΔS为钢丝绳伸长变化量,m为施加的载荷,Δm为施加的载荷变化量,L为钢丝绳长度,E为钢丝绳的弹性模量,a为钢丝绳截面积。
由式(2)和(4)可得升降台换向时钢丝绳伸长变化量:

升降台换向误差包括两种:
(1)上升换向误差
该误差产生于升降台“下降—停止—上升”过程,下降时钢丝绳受力小,而上升时钢丝绳受力大,在下降到上升转换过程中阻力大小先逐渐减小后增大,方向由图3(b)中方向向上变化为图3(a)中方向向下。升降台由静止到上升过程中,在钢丝绳伸长量增加ΔS范围内,升降台仍保持静止,导致上升时出现误差。
(2)下降换向误差
该误差产生于升降台“上升—停止—下降”过程,与(1)中情况相反,钢丝绳受力将减小,阻力大小先逐渐减小后增大,方向由图3(a)中方向向下变化为图3(b)中方向向上。升降台由静止到下降过程中,在钢丝绳伸长量减小ΔS范围内,升降台仍保持静止,导致下降时出现误差。
换向误差仅出现在升降台运行方向改变后第一次运行中,而继续运行时位置控制较为准确。
4 升降台误差补偿
4.1 零位补偿
为确定升降台统一的零点位置,在机械限位开关上方设置一平面,称为电气零点。升降台由机械零点位置上升到电气零点称为零位补偿,上升的距离称为零位补偿值,该值通过实际测量得到,具体方法如下:
(1)升降台以较低速度下降,直至触碰到停止限位开关,此处位置为零;
(2)使用水平仪测量当前升降台的标高,为减小误差,均测量升降台的中心位置;
(3)以中间的升降台作为基准,控制其上升直至达到设定的高度(如设定上升100 mm作为电气零点,通过水平仪观察标尺以确定位置),其余升降台达到标尺相同位置即可,分别记录每台升降台上升的高度,作为到达基准平面的零位补偿值。
当升降台运行到电气零点后,将其位置清零,作为进行位置控制的零点。
4.2 换向补偿
升降台进行零位补偿后已经完成对上升换向误差的补偿,继续上升时控制较为准确。
升降台进行下降换向时按照如下步骤测量补偿值:
(1)在升降台上固定标尺,使用水平仪观察标尺读数,记录为h1;
(2)控制升降台下降一段距离h(如200 mm),记录标尺读数h2;
(3)按照式(6)计算补偿值δ;

(4)验证补偿值δ是否准确
①控制升降台上升一段距离,记录停止时标尺读数h3;
②控制升降台下降距离h+δ,记录标尺读数h4;
③按照式(7)进行计算,其中ε为误差容许值,通常取ε=1 mm。若在容许范围内,则认为补偿准确,否则根据差值修正补偿值,然后再重复步骤(4),直至符合式(7)。

由第3节中分析可知,升降台上升换向为下降换向的逆过程,因此,补偿值相同。升降台在上升与下降过程中设定高度与实际高度的关系如图4所示。经零位补偿后,升降台位置为零,此时已换向,继续上升时钢丝绳拉力变化不大,实际高度与设定高度近似为正比例关系;下降时,需先下降换向补偿值δ升降台才开始下降,之后再次下降时实际高度与设定高度近似为线性关系。例如,升降台上升到高度h',设定高度应为h';下降到高度h',设定高度应为h″,且满足式(8)。

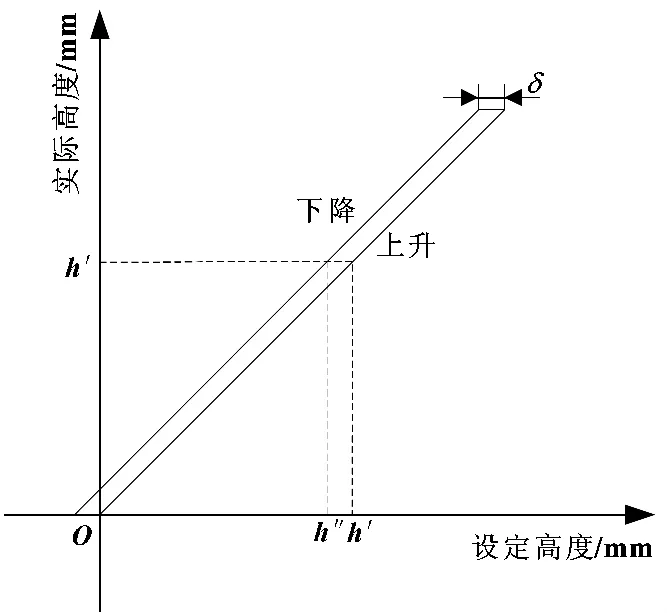
图4 升降台设定高度与实际高度关系
5 升降台位置控制实验
以镇江大型水景秀《白蛇传》的40个水中升降台控制为例,复位至机械零点后,取上升100 mm为电气零点,逐台测试到达电气零点的零位补偿值。然后,测量换向补偿值,其中前10台升降台的测试结果如表1所示。表中可以看出零位补偿值与设定的上升值100 mm相差较大,这是由于限位开关安装位置不同及上升换向误差综合因素造成的结果;换向补偿值的差异原因在于升降台的运行阻力及钢丝绳长度不同。表2为升降台进行位置控制的测试实验,10个升降台分别上升和下降3 700 mm,使用水平仪测量实际运行的高度,从表中数据可以看出,位置控制误差较小。

表1 升降台零位补偿值和换向补偿值

表2 升降台位置控制测试
任选一个升降台进行位置控制的实验,升降台从电气零点开始,先逐渐上升再下降,每次高度差为1 000 mm。在升降台上固定标尺,使用水平仪观察并记录每次的标尺读数,并计算相邻两次读数的高度差。表3为以B4#升降台为例测试的数据,可以看出定位误差在±2 mm范围内,符合设计要求。
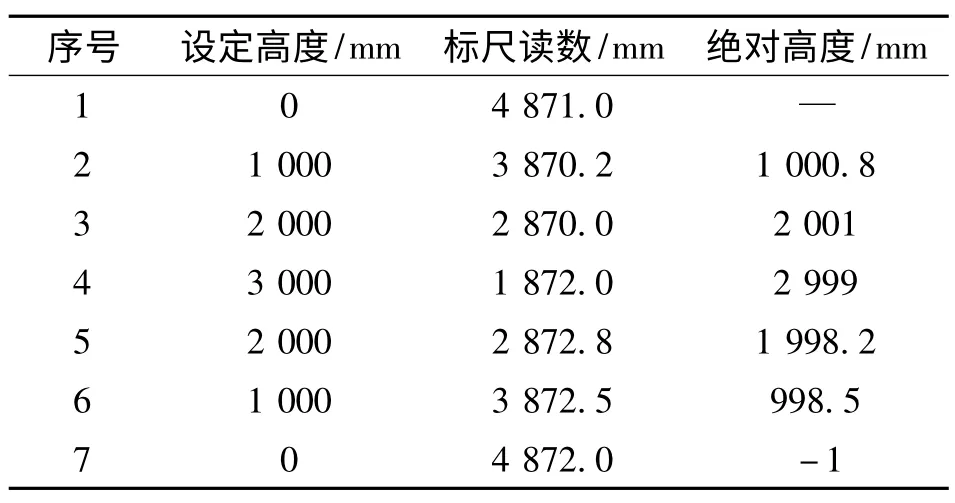
表3 B4#升降台位置控制测试
升降台运行场景图如图5所示,其中,图5(a)为40个升降台位于同一高度,呈现平面,图5(b)为凹形场景图。从图中可以看出,位置控制较为准确,能够满足演出需求。

图5 升降台运行场景图
6 结束语
针对水下升降台远程驱动的特点,设计了控制系统结构。分析影响升降台位置控制精度的因素,设计了一种基于补偿的位置控制方法,通过测量零位差值和换向误差,进行零位补偿和换向补偿以提高定位精度。该方法不用建立复杂的控制模型且易于操作实现,实践证明可有效地提高水中升降台的位置控制精度。
[1]刘基顺,吴涧彤,杨永魁.舞台机械控制系统功能及性能分析[J].演艺科技,2012(3):1-5.
[2]吕圣龙.武汉琴台大剧院的舞台机械[J].艺术科技,2010(2):3-13.
[3]袁溪泽,齐向东.基于PLC的升降舞台同步模糊控制系统研究[J].工业仪表与自动化装置,2012(3):98-101.
[4]崔皆凡,邢丰,赵楠.基于模糊控制器的改进耦合多电机同步控制[J].微电机,2011,44(3):75-77,120.
[5]张承慧,石庆升,程金.一种多电机同步传动模糊神经网络控制器的设计[J].控制与决策,2007,22(1):30-34.
[6]张承慧,石庆升,程金.一种基于相邻耦合误差的多电机同步控制策略[J].中国电机工程学报,2007,27(15):59-63.
[7]刘星桥,胡建群,周丽.自抗扰控制器在三电机同步系统中的应用[J].中国电机工程学报,2010,30(12):80-85.
[8]刘然,孙建忠,罗亚琴.基于环形耦合策略的多电机同步控制研究[J].控制与决策,2011,26(6):957-960.
[9]范岩.多电机同步控制策略的改进[J].机电工程,2007,24(6):65-66,82.
[10]李磊,刘日良,张承瑞.基于工业以太网冗余舞台控制系统研究[J].计算机测量与控制,2012,20(9):2396-2398.
[11]李旭宁,彭思远,吴涧彤.舞台自动控制系统设计与冗余技术研究[J].电气传动,2009,39(8):58-60.

