基于等熵原则的抽蓄电站过渡过程压力数据分析

张 飞，宫 奎，潘 虹，丁景焕

（1.国网新源控股有限公司技术中心，北京 100161； 2.河海大学 能源与电气工程学院，江苏 南京 210098）

1 研究背景

过渡过程试验是校核水轮机调节系统品质的关键性试验，尤其是甩负荷试验对机组旋转部件和引水通流系统将产生很大影响［1］。过渡过程试验过程中一方面将在流道系统中产生大的压力波动，另一方面将在水轮机过流部件中产生很大的压力脉动。压力波动通常具有典型的低频特征，其波动周期取决于流道系统的惯性时间常数、调压室设置及参数等，而压力脉动则与水轮机的工况点转换时流态急剧变化具有直接关系。过渡过程试验时主要的测量参数包括工况参数，如转速、开度、功率等，以及反映机组稳定性参数变化的诸如振动、摆度及压力脉动等。目前的技术手段可以实现对工况参数测量结果的准确分析与评价，而对于稳定性参数的测量与评价则存在诸多难点，其中尤以过流部件压力测量与评价最为突出。受限于材料强度，过渡过程中压力极值导致的结构瞬时应力应在一定的限值范围内并保有余量，同时其疲劳情况应保障材料在服役期内的安全。因此，在大波动过程、小波动过程以及水力干扰过程中均需要对压力极值进行测试以评估通流部件的安全性。

过渡过程压力评估中，高压断面主要考量压力的最大值，低压断面主要是压力的最小值。压力测点的设置情况受限于电站及机组设计，或测点埋于混凝土中通过长测量管路引出产生管路共振，或测点通过非刚性测压管路引接使压力衰减等，导致准确获得压力极值存在困难［2］。同时，数据采集过程中也不可避免受到各种噪声的污染［3］，这也为准确获得压力极值产生了很大限制。调节保证计算模型方面，普遍采用怀利和斯特里所提出的求解水力机械过渡过程的理论和计算机求解方法［4］，这一模型做了很多近似处理，如：一元非恒定管道流动方程中摩阻项的简化，电站各边界层的简化等。在水泵水轮机过渡过程计算时还需要采用水轮机静特性曲线代替动特性曲线，且不考虑各个断面内的水力学参数差异、水中含气量变化对水锤波速的影响、空化等因素［5］。这些假定条件下过渡过程计算获得的数据并不能够与现场测试结果吻合，因此水电水利规划设计总院发布了针对调节保证计算的暂行规定，考虑计算误差对计算结果进行了适当修正，然而这并未完全解决计算结果与试验结果的一致化比较问题［6］。上述分析表明：如何对测试数据进行分析，搭建试验测试结果与调节保证模型计算之间的桥梁，以实现对调节保证计算模型的有效性进行验证，是工程技术人员必须面对的问题。基于此，本文以仙居抽水蓄能电站甩额定负荷压力测试数据为例，引入排列熵和经验模态分解方法对数据进行分析，提出了等熵准则，从而实现调节保证计算模型的评价。

2 基本方法

2.1 排列熵信号分析中的熵是表征信号复杂程度的度量方式。对于给定时域信号，大熵值表明时序中所含信息丰富，复杂性强，而小熵值则相反。常用的熵有排列熵［7］、近似熵［8］、样本熵［9］（Permutation Entropy，PE）等。在众多熵中，排列熵来源于信号本身，对信号没有任何假定，相较于其他熵具有对噪声鲁棒性强的优点，且由于算法简单，适用于处理大样本数据。过渡过程试验过程中，根据相关标准，试验数据的采样率通常在几百至几千赫兹之间，采样持续时间在几十秒至几百秒之间，因此数据量较大，适用于排列熵对其进行分析。

以嵌入维数m和时间延迟τ对时间序列{xt}t=1…T进行相空间重构得到：

将X（i）的m个向量按照升序排列，得到一组新的序列S（g）={j1，j2，…，jm}，其中g=1，2，…，k，k≤m!。根据排列组合原理，这个序列共有m!种不同排列方式。然后计算每种符号序列出现的概率为Pg，则时间序列{xt}t=1…T的排列熵定义为：

上式在Pg=1/m!时达到最大值，因此将排列熵进行归一化处理得到：

归一化后的排列熵范围处于（0，1］范围内，值越大表明信号所含信息量越丰富，信号的复杂程度也高，随机性越强。

2.2 经验模态分解经验模态分解（Empirical Mode Decomposition，EMD）是N.E.Huang等［10］提出的一种将非线性、非平稳信号分解成一系列调频调幅信号的自适应分解方法。该方法特别适用于对非线性、非稳态信号进行分析，在微弱信号提取［11］、信号噪声抑制［12］、故障诊断［13］等领域获得了广泛应用。对一个给定的信号x（t），EMD通过将信号分解成N个本征模态函数（Intrinsic Mode Function，IMF）ci（t）与残差rN（t）的和，即：

为方便起见，称第i次分解结果为第i阶本征模态函数。根据文献［10］，低阶的本征模态函数代表了高频成分，高阶的本征模态函数代表低频成分，即：随着阶数的提高，本征模态函数所表征的信号频率成分逐渐降低。信号的残差作为信号的趋势项亦可以看作是一个高阶的本征模态函数。

3 方法应用

3.1 仙居电站参数仙居抽水蓄能电站采用立轴、单机、混流可逆式水泵水轮机，水轮机工况额定出力382.7 MW，额定水头428 m，额定流量96.34 m3/s，额定转速375 r/min；水泵工况最大净水头492.33 m，相应流量85.51 m3/s，最小净水头421.86 m，相应流量92.75 m3/s，吸出高度-71 m。调节保证要求蜗壳中心线处最大压力值不超过7.31 MPa，尾水管进口与出口处最低压力不小于0.0 MPa，尾水管进口处最高压力不大于1.6 MPa，尾水管出口处最高压力不大于1.7 MPa。

图1 仙居电站4台机组甩100%负荷时计算蜗壳末端压力变化曲线

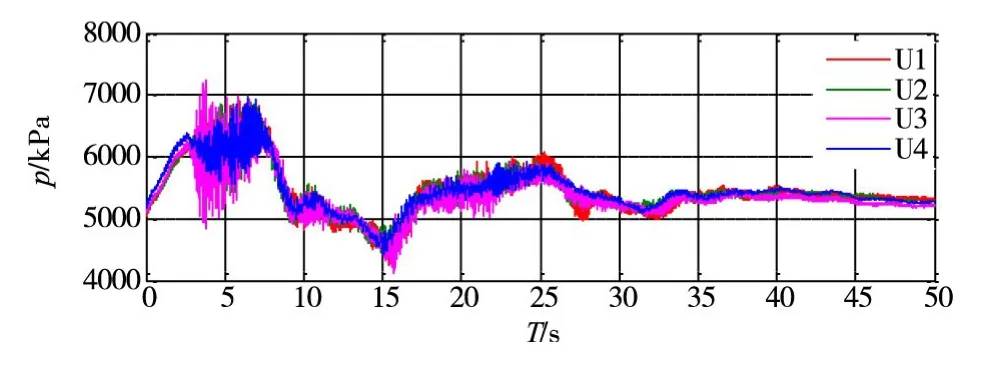
图2 仙居电站4台机组甩100%负荷时实测蜗壳末端压力变化曲线

3.2 甩负荷试验甩负荷工况是调节保证计算重要的工况之一。通常调节保证计算是在给定的特征水头下完成。理论上，甩负荷试验应在相对恶劣工况下实施，以验证调节保证是否满足机组运行要求。然而，单机甩负荷试验受限于上下库水位，通常在试验阶段的当前水位条件时实施。对于典型的一管双机相继甩负荷试验，由于具有很大的破坏性及其不确定性，且发生这种工况的几率极小，通常电站并不实施该项目。甩负荷试验实施时，先由制造厂家、设计院或第三方机构给出当前上下库水位条件结合实测导叶关闭规律下的调节保证计算结果，进而采用试验进行验证。根据标准［14］，甩负荷试验应在25%、50%、75%和100%4个负荷点进行试验，考虑到甩100%负荷是对机组相对较为严苛的负荷点，具有典型性，因此本文以此工况点进行分析。图1为仙居电站4台机组根据实际导叶关闭规律校核的甩100%负荷时蜗壳末端压力计算曲线，图2给出了相对应的实测压力变化曲线。图1和图2分别给出了50 s的计算数据和实测数据，均以导叶动作关闭时刻为零点。

图1中4台机组蜗壳末端压力曲线略有差异，主要原因在于：（1）每台机组的导叶关闭规律存在差异；（2）每台机组试验时的水文情况存在差异；（3）机组位置差异导致的水道参数差异等。实际机组甩负荷后导叶根据预设的关闭规律执行，同时进行球阀的关闭操作，而球阀的关闭时间大于导叶关闭的时间。因此蜗壳末端压力在球阀关闭后趋近于尾水压力，故图2中为方便比对，仅给出了球阀关闭前的50 s数据，这一时段内，球阀的过流能力没有显著变化，不影响甩负荷过渡过程计算。试验数据采样率1200 Hz，满足标准要求［15］。

3.3 压力的熵特性图1中的蜗壳末端压力计算基于特征线法，采用弹性水击数学模型［16］得到。模型中假定通流部件为刚性、忽略各个断面内的水力学参数差异、不考虑水中含气量等因素，因此计算结果中压力曲线较为光滑。分别计算4台机组甩负荷过程理论与实测蜗壳末端压力值的排列熵与极值，结果见表1所示。

表1可见，实测蜗壳末端的压力值与计算值之间存在很大差异，实测最大值显著大于理论计算值，实测最小值亦显著小于计算最小值。这在排列熵中反映尤为明显：模型仿真结果的排列熵显著小于实测数据结果，实测信号的熵值均大于0.6，而模型计算结果均小于0.3，进一步说明了试验数据的复杂性远高于调节保证计算仿真数据。由模型仿真所获得的数据是由确定的数学模型根据既定的水泵水轮机全特性曲线和边界条件而获得，相比较实测信号，限于数学模型的众多假定条件，模型仿真不能完全反应实际情况，因此获得的压力曲线所包含的信息量少；而试验数据则受到多种因素影响，包括测量条件（蜗壳末端压力测点受限于现场条件需采用长引水管路引出，然后进行压力测量）、数据采集中的噪声［17］、通流部件的物理条件等，是多因素下的综合，因此试验数据所包含的信息量远大于模型仿真数据。因此造成两者之间偏差的本质是实测信号与计算结果信息量不一致。

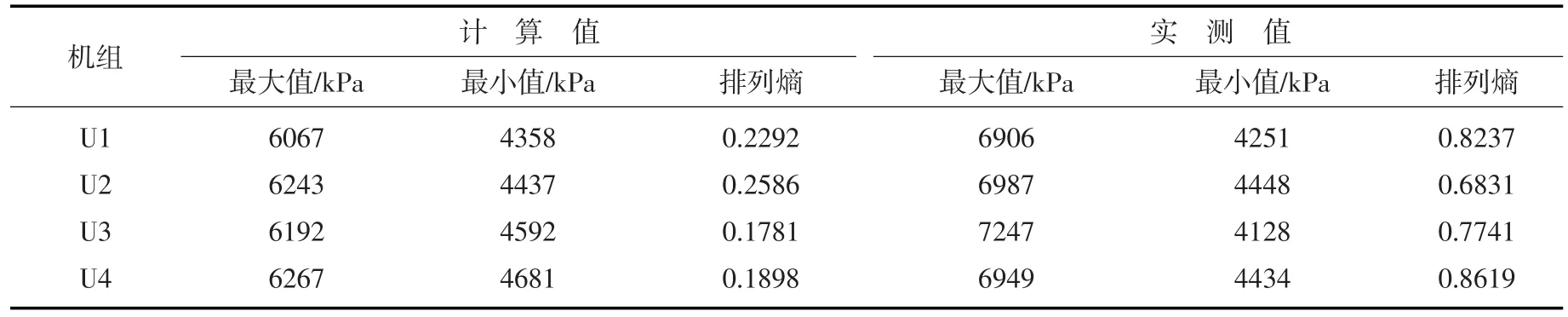
表1 蜗壳末端压力统计值与排列熵值

在机组设计阶段，调节保证计算的准确性直接影响材料的选择及结构设计；而在机组调试阶段，过渡过程试验的结果则直接影响机组是否能够安全投产运行，对电站的经济效应产生显著影响。因此，为解决测试与计算结果之间由于所含有信息量不一致产生的偏差问题，针对不同型式机组，相关组织机构给出了一系列计算结果的修正［18］。然而，对于抽水蓄能机组，由于转轮具有扁平的流道特性，与常规机组具有明显的差异性，实测数据结果与计算结果的对比仍缺乏统一有效的评价手段。考虑到计算结果与实测结果截然不同的熵特性，一种有效的对比方式是：在保持调节保证计算结果与实测试验数据结果的熵一致基础上，对实测值进行处理，获得试验数据的趋势项，对模型的有效性进行评价，进一步获得脉动项，并实现试验数据的评价。

3.4 实测数据的等熵提取以仙居4号机组蜗壳末端压力信号为例进行经验模态分解，分解终止条件根据文献［19］确定。为其分解结果见图3所示，表2给出了每阶本征模态函数对应的排列熵。图3可见：随着本征模态函数阶数的增大，每层所含的频率成分逐渐向低频靠拢，本征模态函数所含有的信息量逐渐减小，导致排列熵值逐渐减小。

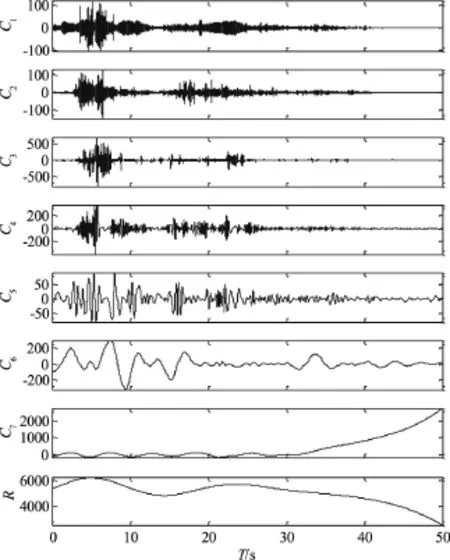
图3 仙居电站4号机组甩100%负荷时蜗壳末端压力EMD分解结果

表2 4号机组蜗壳末端压力各阶本征模态函数排列熵值

针对实测信号，考虑频率成分在本征模态函数之间的传播以及相应的排列熵特性，经验模态分解之后的各阶本征模态函数为Ci，以仿真数据的排列熵Hs为基准，采用如下方法获得与仿真数据排列熵一致的蜗壳末端压力信号：

（2）设定步长δ，排列熵收敛误差ΔH为，计算信号yn(t)=xK(t)+nδCN-K-1的排列熵 Hy，当＜ΔH时停止计算，此时获得n=N，相应的yN（t）即为最终结果。

步骤（1）为反向合成过程，从高阶本征模态函数向低阶本征模态函数反向合成，并计算合成信号的排列熵，直至合成信号的排列熵与模型仿真数据的排列熵接近且相差一阶本征模态函数。步骤（2）为精细求解过程，对合成信号按指定系数重复叠加低一阶的本征模态函数，并计算排列熵值，直至合成信号与模型仿真数据的排列熵一致。

在步骤（2）中为获得精确的等熵信号，可以将步长δ设定为较小的数值，典型如0.001。

以案例机组蜗壳末端压力实测信号为例进行等熵曲线提取，步骤（1）和（2）的收敛过程曲线分别见图4所示，收敛得到蜗壳末端压力曲线见图5所示。图5中同时给出了相同水文条件和导叶关闭规律下模型仿真结果以便于对比分析。

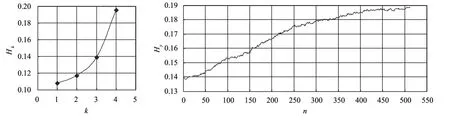
图4 蜗壳末端压力等熵数据收敛过程

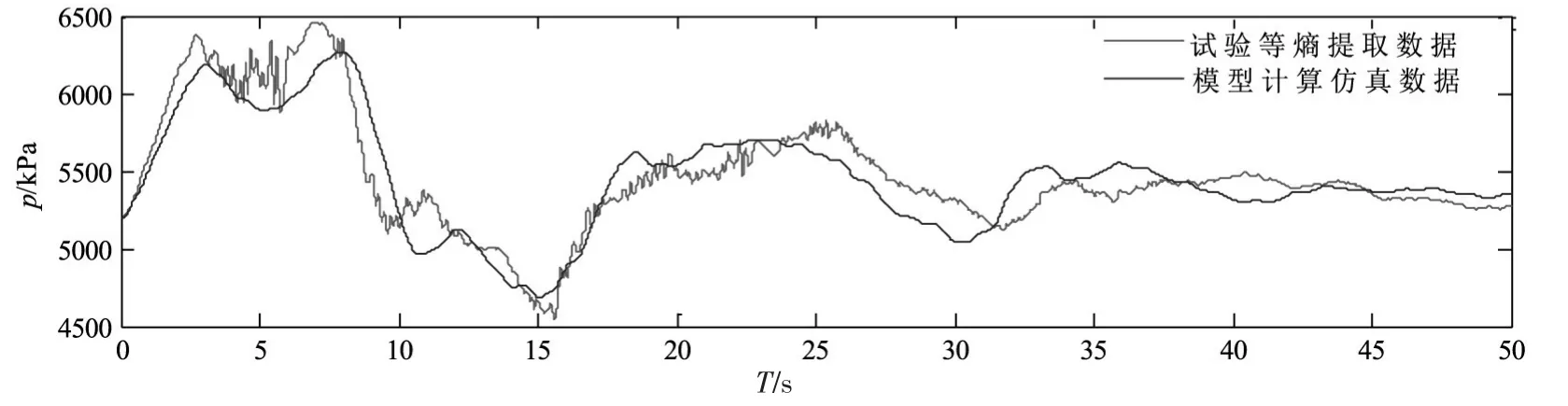
图5 试验等熵蜗壳末端压力曲线与模型仿真数据对比

图4中可以看到：在等熵数据的提取过程中，随着阶数的减小（构成试验提取数据的本征模态函数增多），合成信号的熵值逐渐增大，信号的复杂度逐渐提高，直致获得与模型计算仿真一致的等熵数据，这表明采用本文算法可以收敛到与仿真模型等熵的试验数据。图5中可以看到：试验等熵提取数据与模型计算仿真数据的趋势基本一致，通过相关系数进行验证表明实测数据与模型计算仿真数据之间的相关系数为0.8254，试验等熵提取数据与模型计算仿真数据之间的相关系数为0.9975，因此采用等熵算法提高了模型计算仿真数据与现场实测数据之间的一致性。蜗壳末端压力等熵试验提取数据的最大值为6460 kPa，最小值4546 kPa，对比表1中模型计算仿真结果，两者基本一致，相互之间的误差小于3%；各极值发生的时间亦基本一致，进一步表明了算法的有效性。采用试验等熵提取数据对模型计算结果进行校核的益处在于：受限于试验数据获取过程中一系列不可控因素，试验数据的熵值显著高于仿真数据，对两组不同方法获得的数据直接进行比较将导致结果偏差大，等熵原则意味着两个信号所包含的信息量一致，而采用经验模态分解方法进行反向合成时，随着数据的不断融合，信号中含有的频率成分逐渐增多，信号的复杂度提升，是一个熵增的过程，通过这个过程提升了测试数据的质量。等熵原则在试验和仿真之间构建了准则，确保两者具有相同的比较基础，从而使得对比结果更具有可操作性。

图5中试验等熵提取数据的波动情况大于模型仿真数据，导致这一因素的主要原因在于：模型计算数据的时间步长一般取值0.01 s，而试验数据的采样率为1200 Hz，等效时间步长为0.00083 s，因此试验数据的采样率远大于模型计算数据的采样率，这导致试验数据中含有更多的组合情况，从而使得信号的复杂性进一步提高。

图6给出了原始采样与等熵试验数据两者之间的差值曲线，称之为脉动项曲线。从该图中可以看到从原始试验数据中提取等熵试验数据后的脉动项在整个甩负荷过程中的变化情况。计算其排列熵为0.8345，这表明脉动项中所包含的信息成分非常丰富。由于甩负荷过程是典型的非稳态时变过程，因此采用短时傅里叶变换进行分析［20］。对原始采样数据与脉动项数据分别进行短时傅里叶变换，变换时窗口长度为2 s，步长为0.2 s，采用汉宁窗函数进行加窗，变换结果见图7所示为方便观测，图7中的幅值坐标采用对数进行显示。从图7可以看出：除低频部分外，原始数据与脉动项的频谱基本一致，均包含与转速密切相关的动静干涉与叶片通过频率成分，因测压管路特性并由特性转速所激励的管路共振频率等，且这些频率成分所对应的幅值基本一致。这表明采用等熵方法能够分离出频率成分丰富的脉动项数据，而脉动项所反映的数据正是调节保证模型所不能评估的部分。

图6 脉动项曲线

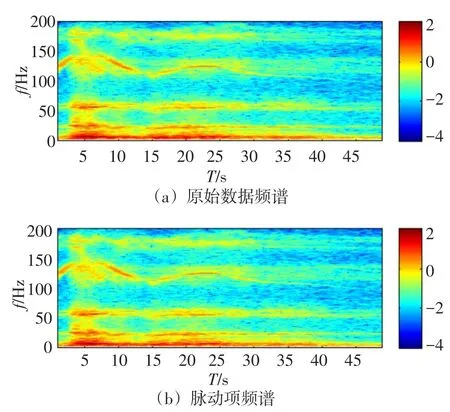
图7 原始测试数据与脉动项频谱

4 结论

为解决抽水蓄能机组过渡过程工况调节保证验证时真机试验实测压力数据与调节保证模型计算数据偏差大的问题，以仙居电站4号机组甩额定负荷时的蜗壳末端压力数据为例，引入排列熵计算压力信号的复杂性，对压力信号进行经验模态分解，获得了各阶本征模态函数。在此基础上，采用排列熵计算信号的复杂性，基于等熵原则对试验数据的各阶本征模态函数进行反向合成，从而得到试验等熵提取数据，并与调节保证模型仿真计算进行对比，研究结果表明：试验实测数据与调节保证计算结果之间的差异本质上是由于两者之间的信息量不一致所产生；采用等熵原则构建的试验等熵提取数据与模型仿真计算结果具有良好的一致性；等熵原则解决了调节保证验证时实测信号与计算结果信息量不一致导致的结果不确定性问题。