基于AquaCrop和NSGA-Ⅱ的灌溉制度多目标优化及其应用

宋 健，李 江，2，杨奇鹤，毛晓敏，杨 健，王 凯

（1.中国农业大学 中国农业水问题研究中心，北京 100083；2.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084）

1 研究背景

在水资源短缺的干旱、半干旱地区，用水矛盾突出，农业灌溉可用水量逐渐减少［1］，如何在非充分灌水条件下制定合理的灌溉制度，对于提高该地区农业水分利用效率和促进农业可持续发展具有重要意义。

灌溉制度优化是合理制定非充分灌水条件下灌溉制度的重要手段之一，其核心思想是确定有限水量在作物生育期内如何分配，以实现作物产量最大或效益最高的目标。灌溉制度优化方法主要包括线性规划、非线性规划及动态规划等，其中应用较多的是动态规划方法［2］。这些方法大多以生育阶段、月、旬为时间尺度，解决不同阶段间的水量分配问题，以达到产量最大或效益最大的目的［3］。但这些方法对不同灌溉制度下的农田蒸散发过程及其对作物产量的影响考虑比较简单，很难客观反映出不同灌水条件下的产量变化，同时很难确定具体的灌水日期。作物生长模拟模型可以模拟不同灌水条件下的作物产量变化，将模拟模型与优化模型相结合对作物灌溉制度进行优化为解决上述问题提供了有效途径。

灌溉制度模拟-优化模型多采用Jensen水分生产函数模拟作物产量［4］，通过经验公式将Jensen函数的敏感指数降至日尺度，结合水量平衡模型及一定的优化技术对灌溉制度进行优化求解，以得到产量最大或效益最高的单一优化目标［5-7］。该方法可以较准确地反映不同灌溉制度下的农田蒸散发过程及其对作物产量的影响，同时又可得到具体的灌水日期。然而，以水量平衡及水分生产函数为基础的作物模拟模型，多是基于大量试验数据的分析拟合，并以经验公式表达作物产量，难以从机理上描述不同田间措施（覆膜等）影响下的作物生长过程。基于作物生长过程的模拟模型（CERES模型［8］、SWAP模型［9］和AquaCrop模型［10］等），与传统水分生产函数方法相比，可以更全面地描述土壤水分动态和作物生长发育等过程。

作物生长模拟模型一般具有复杂的计算过程和高度非线性，其计算复杂度要远高于Jensen等水分生产函数，导致优化求解的计算成本较大。此外，该类模型一般是封装好的软件，难以拆分，且需要特定的输入输出文件格式，动态规划法等传统的灌溉制度优化方法将不再适用。以遗传算法为主的进化算法可以克服传统优化方法在此方面的不足，并广泛应用于灌溉制度优化问题中。

随着研究的深入，灌溉制度优化也由追求产量最大或是效益最高的单目标问题向复杂的多目标优化问题演变［11-13］。一般而言，多目标优化问题的多个目标之间存在冲突关系，不存在绝对最优解，只存在Pareto最优解，即该解的目标值向量优于其它可行解的目标值向量，求解多目标优化的一类方法是“事先宣布类”［14］，该类方法要求在求解问题前提供所有决策者的偏好信息。根据这些偏好信息可以将多个目标转换为一个综合目标，从而将多目标问题转换为单目标问题。经过该方法处理后的优化问题可以采用单目标的灌溉制度优化模型进行求解，但该方法的缺陷是不能面向自身偏好不同的决策者。在这种情况下可采用多目标遗传算法，首先求解出大量的非劣解，然后在非劣解中进行决策。在众多多目标遗传算法中，NSGA-Ⅱ应用较为广泛［15］。

作物的产量最大和灌水量最小是多目标灌溉制度优化问题中最主要的两个目标。求解由这两个目标组成的灌溉制度优化问题时会得到灌水总量与产量之间的关系，该关系被定义为“最优水分生产函数”［16］。然而，多数研究是直接将得到的水分生产函数展现给决策者供其决策，对于决策部分的研究较为粗糙［17-20］。这在决策者决策依据模糊时，容易增大决策者的负担，同时也不能预测生产者的灌溉行为，对水资源管理与经济管理造成了一定的阻碍。

因此，本文选用联合国粮农组织（FAO）推出的结构简单、所需参数少、计算复杂度低、精度合理且适用于水资源匮乏地区的作物生长模拟模型AquaCrop，与快速非支配排序遗传算法（NSGA-Ⅱ）相结合，构建出灌溉制度多目标模拟-优化模型，并利用功效系数法对优化结果进行决策。利用位于西北干旱区石羊河试验站不同覆膜条件下春小麦试验数据，对模型进行率定与验证，确定该地区不同典型年不同覆膜处理下春小麦的优化灌溉制度，并为不同规模的用户（农户和农场）提供相应灌溉决策。

2 基于AquaCrop和NSGA-Ⅱ的灌溉制度多目标优化决策模型

基于AquaCrop和NSGA-Ⅱ的灌溉制度多目标优化决策模型包括AquaCrop模拟、作物灌溉制度优化与灌溉制度决策三部分。首先，利用试验数据对AquaCrop模型参数进行率定与验证；然后，在Matlab平台下调用率定验证后的AquaCrop模型对不同灌溉和覆膜条件下作物生长进行模拟，运用NSGA-Ⅱ算法进行优化求解，得到一系列由灌溉制度组成的Pareto集；最后，运用功效系数法对优化结果进行决策，得到最优灌溉制度。

2.1 AquaCrop模型AquaCrop模型的核心思想是Doorernbos与Kassam在1979年提出的D-K模型［21］。AquaCrop模型在此基础上利用冠层覆盖度对土壤蒸发与作物蒸腾进行了区分，然后利用蒸腾量与归一化水分生产效率计算地上生物量，再通过收获指数控制最终产量。其核心公式为：

式中：B为地上生物量，t/hm2；WP*为归一化水分生产效率，根据不同水分生产效率对二氧化碳浓度进行归一化而得到；T为每日蒸腾量，mm；Y为产量，t/hm2；HI为收获指数。

模型的输入模块主要包括作物、气象、土壤、地下水、田间管理和初始条件等。其中，气象模块所需要的输入文件包括降雨、最高最低气温、参考作物腾发量以及二氧化碳浓度。土壤模块则包括土壤的饱和含水率、田间持水量、凋萎系数以及饱和导水率等。田间管理模块主要包括覆膜与施肥等。地下水模块反映地下水埋深变化。初始条件包括初始土壤含水量、冠层覆盖度与地上生物量。模型输出主要包括4部分：作物生育期内的冠层覆盖度发育过程、地上生物量累积过程、土壤含水率变化过程和最终产量。对于该模型的具体描述可参见相关文献［10，22-24］。本研究中，参考作物腾发量由气象数据经Penman-Montieth公式计算得到，土壤初始数据采用田间实测值。由于试验站地下水埋深较深，本文不考虑地下水的影响。田间管理模块对于覆膜的处理，考虑到膜的开孔和破损情况，将其覆盖度设为80%。本研究不着重考虑二氧化碳浓度变化对于结果的影响。根据AquaCrop Reference Manual［24］提供的公式计算，二氧化碳浓度每提高1 ppm，归一化水分生产效率仅会提高0.24%，因此在非气候变化背景下由二氧化碳导致的产量差异将远小于灌溉制度不同所导致的产量差异。同时由于缺少二氧化碳的实测数据，故本文采用AquaCrop中默认的二氧化碳数据。AquaCrop模型认为，在模拟10年之内的作物生长状况时，可以利用该二氧化碳数据［24］。该数据来自MaunaLoa天文台，曾多次在我国西北干旱区的研究中被采用［25-27］，具有一定的适用性。

本文主要采用归一化均方根误差（Normalized Root Mean Square Error）、纳什效率系数（Nash-Sutcliffe Efficiency Coefficient）与决定系数对模型模拟值与实测值之间的吻合程度进行评判。各指标的计算方式为：

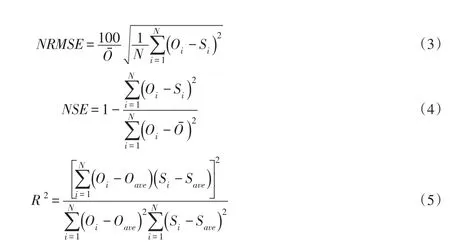
式中：NRMSE为归一化均方根误差；NSE为纳什效率系数；R2为决定系数；Oi为实测值（i=1，2，…，N），Si为模拟值（i=1，2，…，N），Oave为所有观测值的平均值；Save为所有模拟值的平均值；N为数据个数。

2.2 优化模型及求解算法

2.2.1 优化模型 本研究的优化目标为作物产量最大及灌水总量最小，决策变量为灌水日期及每次灌水量，约束条件为每次灌水的灌水日期和灌水量，其数学形式为：

式中：Y为作物产量，t/hm2，取决于灌溉制度（灌水日期和灌水定额），由AquaCrop模型模拟得到；D=［d1，d2，…，dn］表示灌水日期di（i=1，2，…，n）按先后顺序组成的向量，n为灌水次数；I=［I1，I2，…，In］表示每次灌水相应的灌水量，W为灌溉定额，mm；Imin、Imax分别表示每次灌水的最小、最大灌水量，mm。

2.2.2 NSGA-Ⅱ算法 本文采用改进型非支配排序遗传算法（NSGA-Ⅱ）［28］对优化模型进行求解。NS-GA-Ⅱ是在非支配排序遗传算法（NSGA）［29］中引进精英策略以扩大采样空间，并采用拥挤度和拥挤度比较算子，使结果能够快速均匀地收敛于Pareto最优解集。该算法具体包含6个步骤：种群初始化、非支配排序、拥挤距离的计算、选择、交叉与变异和重组与选择。本研究首先随机生成初始灌溉制度，然后对其中的灌水日期进行排序，生成具有正常灌水顺序的初始解，利用该初始解进行交叉及变异等遗传操作，并利用罚函数，减小由遗传操作产生的灌水日期混乱的解的适应度，从而获得理想的灌溉制度优化结果。罚函数P及适应度函数Fitness的最终形式为：

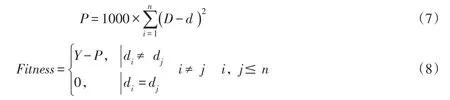
式中d表示经过排序后的日期向量，其它符号意义同上。

对于遗传算法而言，种群越大，遗传代数越多，优化结果越精确，但计算成本也越大。本文在权衡计算精度与计算效率之后，采用50个个体进行500代遗传后的优化结果。

2.3 决策方法本文采用指数型功效系数法［14］对优化结果进行决策。本研究中的灌水定额（I）越大时，认为其功效系数越小；产量（Y）越大时，认为其功效系数越大。计算公式如下：

式中：gY为产量的功效系数；Y为作物产量；Y0为产量的不满意值；Y1为产量的最低满意值；gI为总灌水量的功效系数；I为总灌水量；I0为灌水量的不满意值；I1为灌水量的最低满意值；g为总功效系数，取各功效系数的几何平均。其中，产量与灌水量的最低满意值与不满意值一般参考前人研究或通过调查问卷获取。本文将甘肃省平均粮食产量的最大值与最小值及试验田产量的最大值与最小值设置为农户作物产量及农场作物产量的最低满意值与不满意值，根据当地经验灌水量及优化结果选取灌水量的不满意值及最低满意值。

2.4 灌溉制度多目标优化决策方法本文在Matlab平台下实现灌溉制度多目标优化决策。首先，在Matlab（Ver.R2017a）下调用率定好的AquaCrop模型并输入相应的灌溉制度文件对作物生长状况进行模拟，将得到的产量及总灌水量读取到Matlab中，构建基于AquaCrop和NSGA-Ⅱ的灌溉制度多目标模拟-优化模型，并对模型进行求解；然后，运用功效系数法对优化结果进行决策，得到最优灌溉制度。具体操作流程见图1。

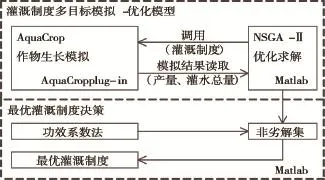
图1 灌溉制度多目标优化决策流程

3 模型应用

3.1 试验设计及数据搜集不同灌水和覆膜处理下的春小麦田间试验于中国农业大学石羊河流域生态节水试验站开展，试验站位于西北内陆干旱区的甘肃省武威市（37°52′N，102°50′E）。小麦品种为永良4号，2014年、2015年分别于3月26日、3月21日播种，不覆膜条件下分别于7月24日、7月19日收获（生育期120 d），覆膜条件下小麦分别于7月14日、7月9日收获（生育期110 d）。试验共设置10个处理：田间管理处理分为膜上穴播、覆膜率80%（M），不覆膜穴播（N）；每种田间处理包括5个水分处理。水分处理分别为：100%灌水量（W1）、100%灌水量减少1次灌浆期灌水（W2）、75%灌水量（W3）、75%减少量1次灌浆期灌水（W4）、50%灌水量（W5），灌溉方式为畦灌。灌水量参照当地灌溉制度制定（表1），其中灌水日期以播后日期表示（DAP）。播种前根据当地经验施底肥（尿素225 kg/hm2与过磷酸钙450 kg/hm2），第一次灌水前追肥一次（尿素150 kg/hm2）。试验观测数据包括气象要素、叶面积指数、地上生物量、土壤特性、土壤含水率以及产量，具体观测方法参见文献［30］。土壤特性的数据见表2。考虑到两年之间温度条件存在差异，本文采用生长度日（GDD）计算作物物候。由于AquaCrop模型输出冠层覆盖度CC，需将观测叶面积指数LAI转换为冠层覆盖度进行对比，转化公式为：

表1 当地经验灌溉制度

表2 土壤物理性质

3.2 优化灌溉情景设定本文在进行灌溉制度优化时，气象典型年通过分析武威站1963—2016年作物生育期内的累积降水量确定，气象数据来源于中国气象数据网（https：//data.cma.cn）。通过优化适线法拟合Pearson-Ⅲ型曲线，确定降水量保证率为25%、50%、75%的年份为丰水年、平水年与枯水年（表3），选择该年份的气温、参考作物腾发量等所有气象数据分别对丰水年、平水年与枯水年的灌溉制度进行优化决策。

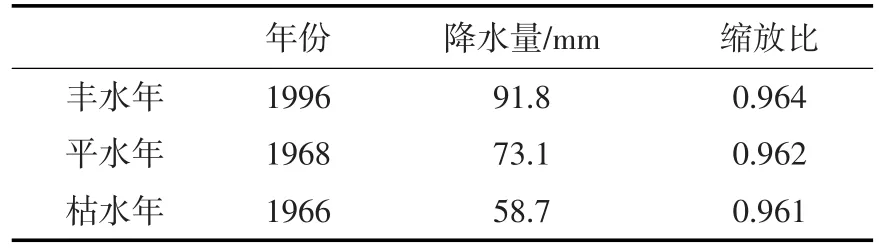
表3 典型年及缩放比

4 结果与分析

4.1 AquaCrop模型率定与验证本文采用2014年试验数据对AquaCrop模型进行参数率定，并利用2015年数据对模型进行验证，结果见表4及图2。结果显示，模型对于产量模拟结果的NRMSE均不超过10%，R2亦大于0.8，认为模型对于产量的模拟具有很高的精度。1 m土层储水量模拟结果的NRMSE均小于20%，认为模型对于土壤储水量变化模拟的精度较好。冠层覆盖度模拟结果的误差指标在两年间差异较大，模型率定结果较为精确，验证结果精度有所下降。2014年冠层覆盖度模拟结果精度减小主要体现在NSE减小，但NRMSE指标仍未超过20%，故认为虽然模拟的冠层覆盖度发育趋势发生变化，但变化不大。模型对于地上生物量的模拟结果均有较高的NSE，说明模型可以很好地模拟生物量的变化趋势；尽管NRMSE变幅较大，但均未超过30%，说明模型的模拟结果可以接受。总体而言，运用率定后的AquaCrop模型用来进行灌溉制度优化，可以满足精度要求，模型率定后的参数见表5。

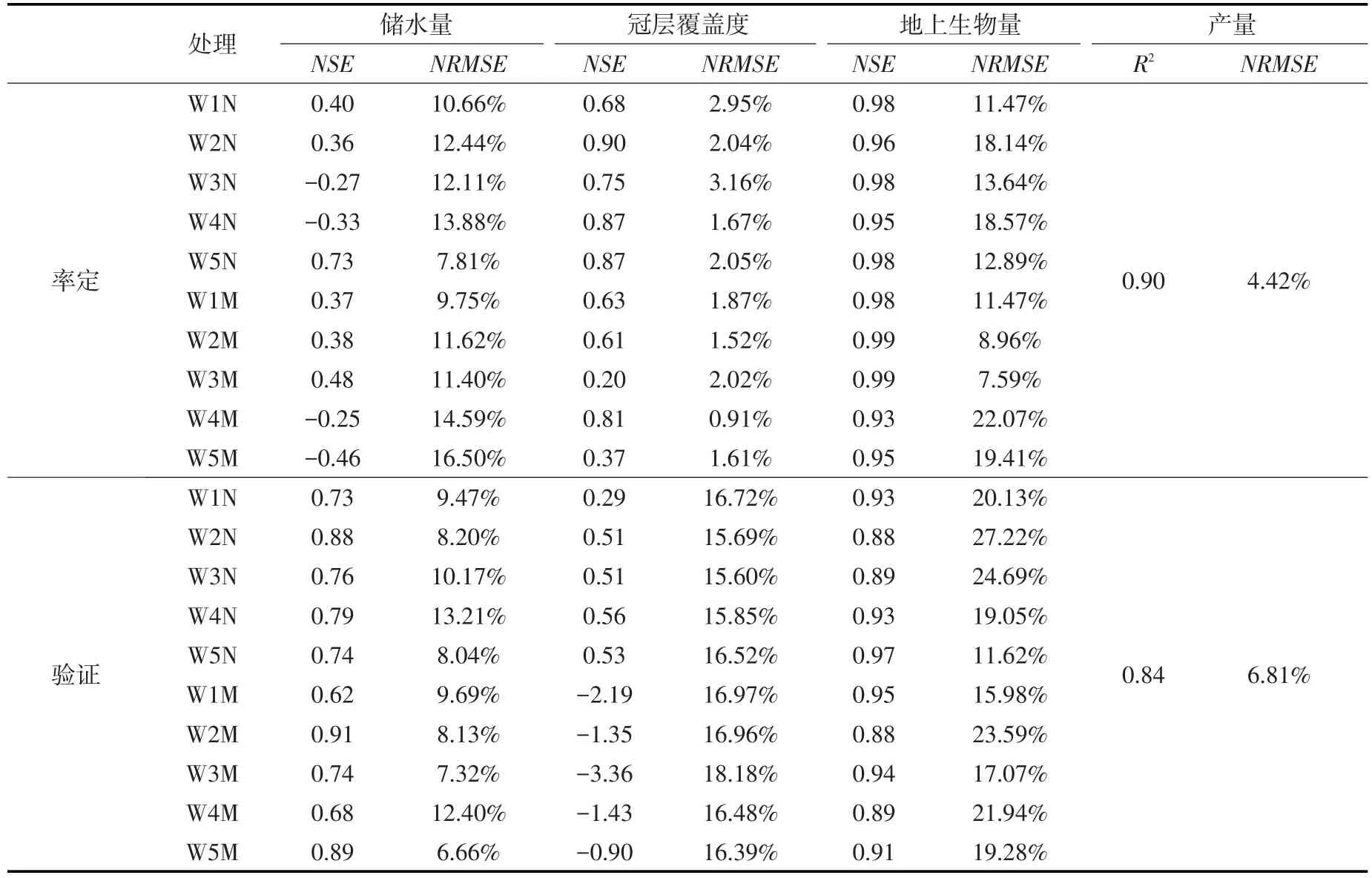
表4 模型率定验证评价指标

W5水分处理下春小麦1 m土层储水量、地上生物量及冠层覆盖度随时间变化趋势见图3。1 m土层储水量的模拟和实测值均显示在灌水后明显升高，随着蒸散发的发生而逐渐降低。2014年第一次实测储水量偏高于模拟值，原因在于第一次测量日期为4月8日，此时试验地区土壤下部尚未解冻，而AquaCrop模型未考虑土壤冻融，导致模型模拟土壤储水量时精度略低。其余土壤储水量实测值与模拟值变化趋势相同，说明该模型可以较好地模拟土壤储水量动态变化。地上生物量模拟结果显示：水分亏缺严重时，不覆膜条件下干物质累积曲线低于覆膜处理，说明不覆膜条件下作物生长易受水分胁迫影响，覆膜具有保墒、缓解作物水分胁迫的作用。冠层覆盖度模拟结果显示：覆膜可以加速作物生育进程，提前作物冠层覆盖度达到最大的时间，生育后期模拟精度明显高于模拟前期。

4.2 灌溉制度优化结果分析灌溉制度优化结果（图4）表现出了两个目标之间明显的冲突关系，即随着灌水量目标的改善（灌水量减小），产量目标在恶化（产量减小）。利用Matlab中的convhull函数可以求出该解集的凸包，对该凸包的右上部分进行曲线拟合即可得到“最优”的水分生产函数。本文中利用一次函数（形如y=ax+b）与二次函数（形如y=ax2+bx+c）分别对水分生产函数进行拟合，在所有情况下，二次函数的拟合结果均优于一次函数的拟合效果。以覆膜条件下的NRMSE为例，平水年分别为0.37%（二次函数）与1.00%（一次函数，后文皆为此顺序），丰水年为0.24%与1.02%，枯水年为0.37%与1.00%。尽管图中覆膜后的水分生产函数在灌水量较小时看上去更接近一次函数的形式，但经过曲线拟合后二次函数仍然表现出了较好的拟合优度。以灌水两次时为例，NRMSE在丰水年0.09%（二次函数）与0.19%（一次函数），平水年为0.20%与0.39%，枯水年为0.11%与0.25%。这说明本研究中水分生产函数更符合二次函数的形式。该类形式的生产函数表明，作物的边际产量随着灌水的增加而逐渐减小，原因在于灌水增加导致土壤棵间蒸发与深层渗漏等水分损耗增大，使水分生产函数表现为这种形式。

相同典型年下覆膜处理能够收获更多的产量，且所需的最优灌水量要小于不覆膜处理下的最优灌水量。原因在于：地膜可以有效的减少地面蒸发，使灌溉水更多消耗于作物蒸腾，最终收获更多的产量。例如在丰水年，覆膜处理小麦最大产量可达到7.56 t/hm2，相比不覆膜处理下增产0.69 t/hm2，且全生育期仅需灌水344 mm，同比不覆膜处理节约26 mm。相同覆膜处理下，平水年条件下小麦的最优产量要高于其它典型年的最优产量，此时覆膜、不覆膜所能达到的最大产量为7.58 t/hm2、7.14 t/hm2；所需灌水量分别为303 mm和343 mm。枯水年覆膜、不覆膜所能达到的最大产量为7.43 t/hm2、6.94 t/hm2，所需灌水量分别为375 mm和453 mm。

图2 模型率定验证结果

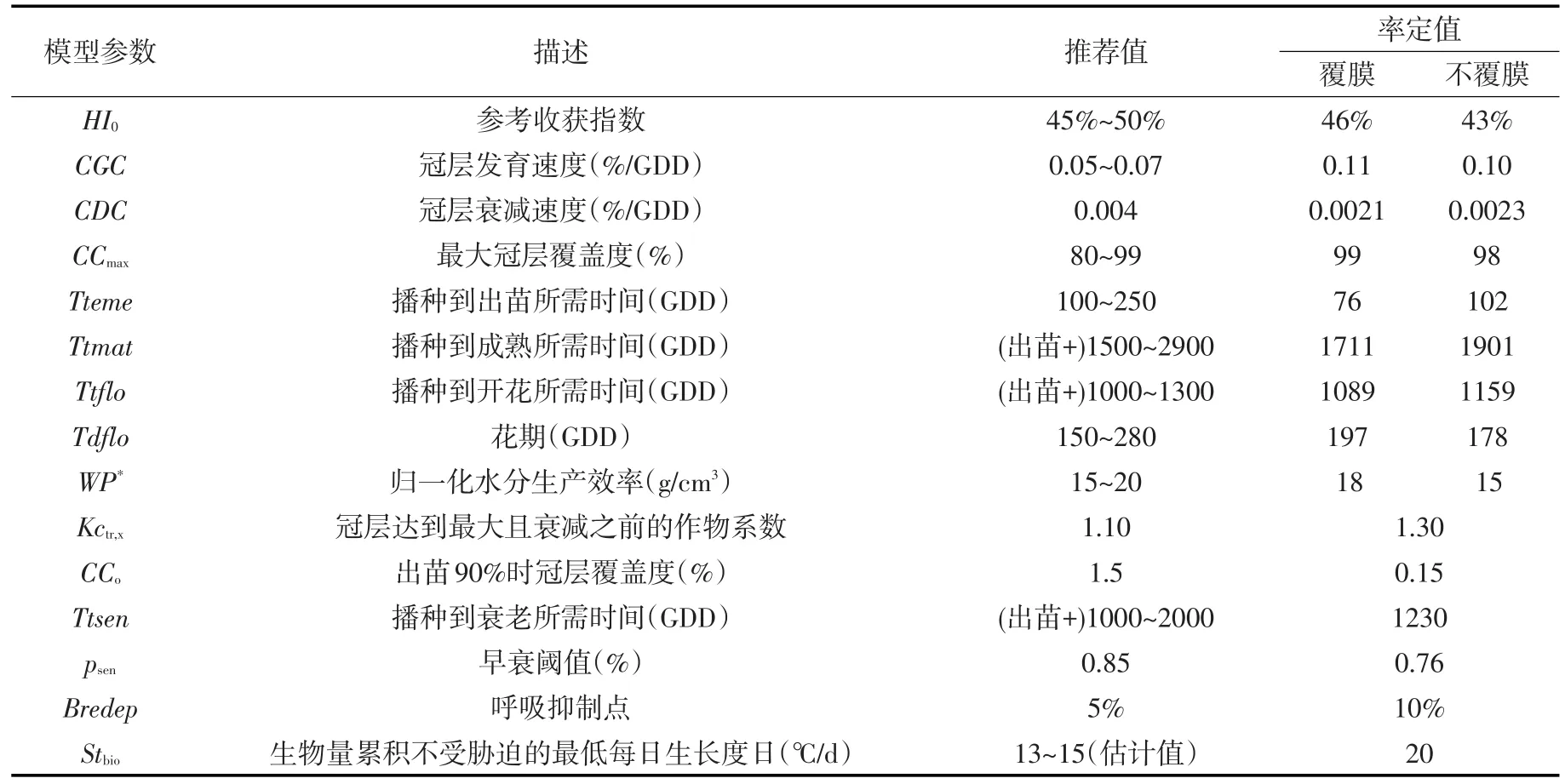
表5 模型参数率定结果

图3 1m土层贮水量、地上生物量及冠层覆盖度随时间变化结果

图5表示覆膜的增产效果随灌水量的变化情况（均采用二次函数表示），结果显示覆膜时的二次项系数要大于不覆膜时的系数，对两个水分生产函数做差可得到一条开口向上的二次函数（a＞0）且灌水量处于对称轴的左半侧，说明覆膜的增产效应随着灌水量的增加而逐渐减少。当灌水量较小时增产效应明显，例如当灌水量为80 mm时，覆膜较不覆膜可以增产约1.3 t/hm2（丰水年1.38 t/hm2，平水年1.31 t/hm2，枯水年1.34 t/hm2）。当灌水量较大时，例如当灌水量为300 mm时，覆膜较不覆膜仅增产0.8 t/hm2左右（丰水年0.87 t/hm2，平水年0.75 t/hm2，枯水年0.82 t/hm2）。

灌水次数会对产量造成影响，当灌水量较小时，灌水次数少的灌溉制度收获的产量更高；当灌水量较大时，多次灌溉会收获更高的产量，这种规律在不覆膜时表现得更为明显。以平水年为例，同样灌溉323 mm水量时，灌水3次所能达到的产量为6.30 t/hm2，灌水4次时，所能达到的产量为6.67 t/hm2；当灌水总量为160 mm时，灌水4次、3次、2次所能收获的最大产量分别为4.03 t/hm2、4.41 t/hm2、4.52 t/hm2，其中灌水2次所获得的产量最高，灌水3次与灌水2次产量相差不大，减产2.4%（相比二水），灌4次时产量差距较大，减产10.8%（相比二水）。当灌水总量为225 mm时，灌4次水、3次水、2次水所能收获的最大产量分别为5.78、5.72和5.52 t/hm2。此时灌水4次获得的产量最大，灌水3次的产量比灌水4次的小但差距不大，仅减产1%，灌水2次时产量最小，比灌4次水减产4.5%。随着灌水量的继续增大，2次灌水已经不能满足要求，在总灌水量为333 mm时，灌水4次的产量为7.10 t/hm2，灌水3次的产量为6.61 t/hm2，相比减产6.9%。这种现象在覆膜时表现得并不明显。这是由于当灌水总量较小时（如160 mm），土壤含水量长期处在较低水平，作物受干旱胁迫较重。若灌溉次数多，会导致单次灌水量较小，难以缓解作物受到的胁迫，进而导致干物质累积与产量形成受阻；当灌水量较大时（如333 mm），灌水次数偏少则会导致单次灌水量较大。一方面，土壤蒸发与土壤含水量呈正相关，单次灌水量越大，灌水后的土壤蒸发也越大；另一方面，单次灌水量越大则越容易产生深层渗漏。因此当灌水量较大时，灌水次数越少产量越高。

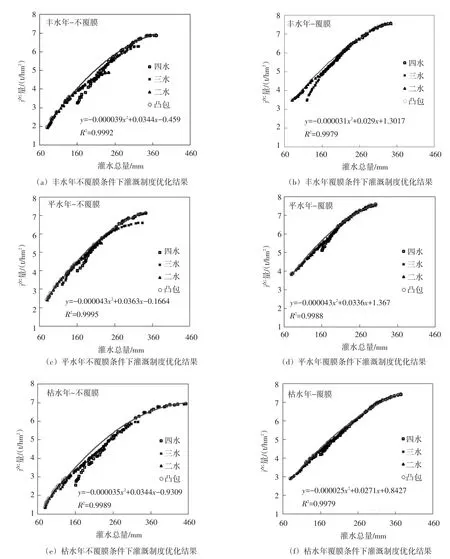
图4 灌溉制度优化结果

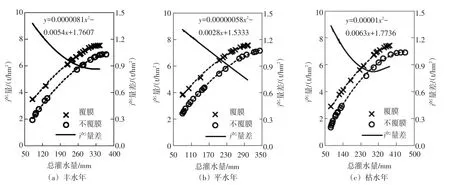
图5 覆膜与不覆膜条件下水分生产函数差值

4.3 灌溉制度决策不同的决策者决策依据与目标各不相同。就种植业生产而言，可以将从业者划分为农户与农场两种类型，两者之间的最大区别在于经营规模与资金投入。农场经营规模大并且全部生产资料都投入到农业生产中。农户则不同，尤其是在农户有了进城务工的选择之后，农户的决策与农场之间产生了本质的区别。农场仍然追求更大的净效益，而农户则要求耕地产出的粮食满足温饱的基础上可以尽量省时省工，以提供更充裕的时间进城务工。

为了反映出这种区别，本文对两者的功效系数进行了区分。农户产量的功效系数设置Y0=3.18 t/hm2，Y1=3.53 t/hm2，该值取自于“十二五”期间甘肃省粮食平均产量［31］的最大值与最小值。假定农场Y0=4.5 t/hm2。Y1=6 t/hm2，该值取自相关文献［32］中的较大值与较小值。同时，由于覆膜在增加产量的同时也增加了生产成本，这将会导致在覆膜时生产者对于粮食的期望产量有所增高，假定其增加值为由地膜成本根据粮价折算出的产量值。小麦价格采用最低收购价2360元/t，地膜投入采用经验值900元/hm2。本文认为农户与农场之间灌水量的功效系数相同，其满意度值大于当地经验灌水量（320 mm），不满意值小于优化结果中的最大灌水量（453 mm），取I1与I0分别为360 mm与450 mm。决策结果如表6、表7所示。

决策结果显示：对于农户而言，最大灌水量为228 mm，得到的最大产量为5.378 t/hm2，大多数情况下灌水3次；对于农场而言，最大灌水量为320 mm，得到的最大产量为7.245 t/hm2，在不覆膜的情况下灌水4次，覆膜的情况下灌水3次。由于农户与农场对于粮食产量的期望不同，农户的灌水量，灌水次数与产量均小于农场，二者对生产行为的决策出现了明显区别，说明通过设定合适的功效系数，可以为不同的决策者提供相应的决策参考。

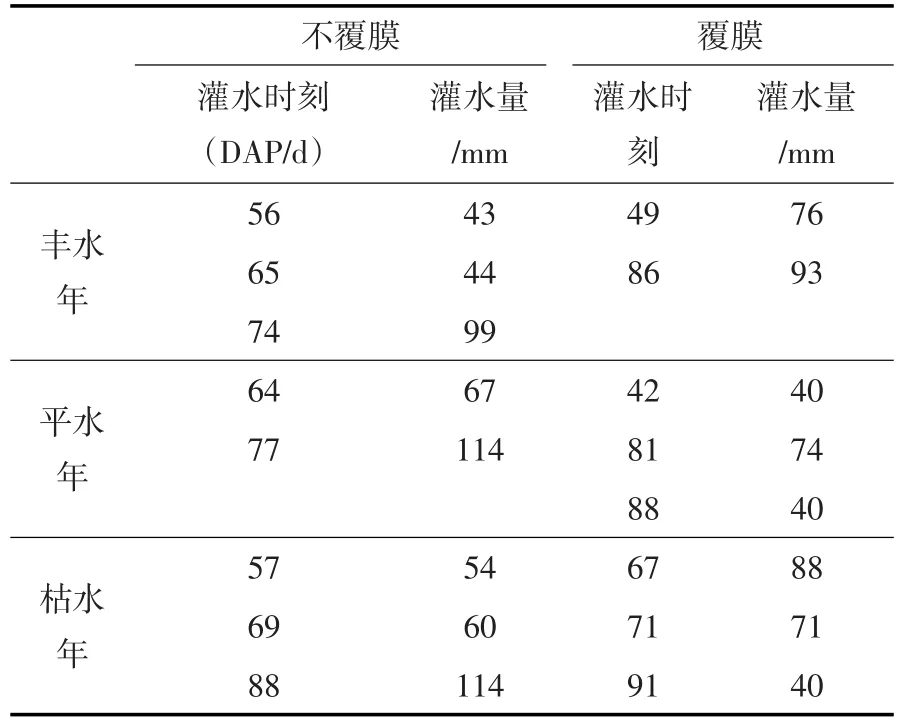
表6 农户决策结果

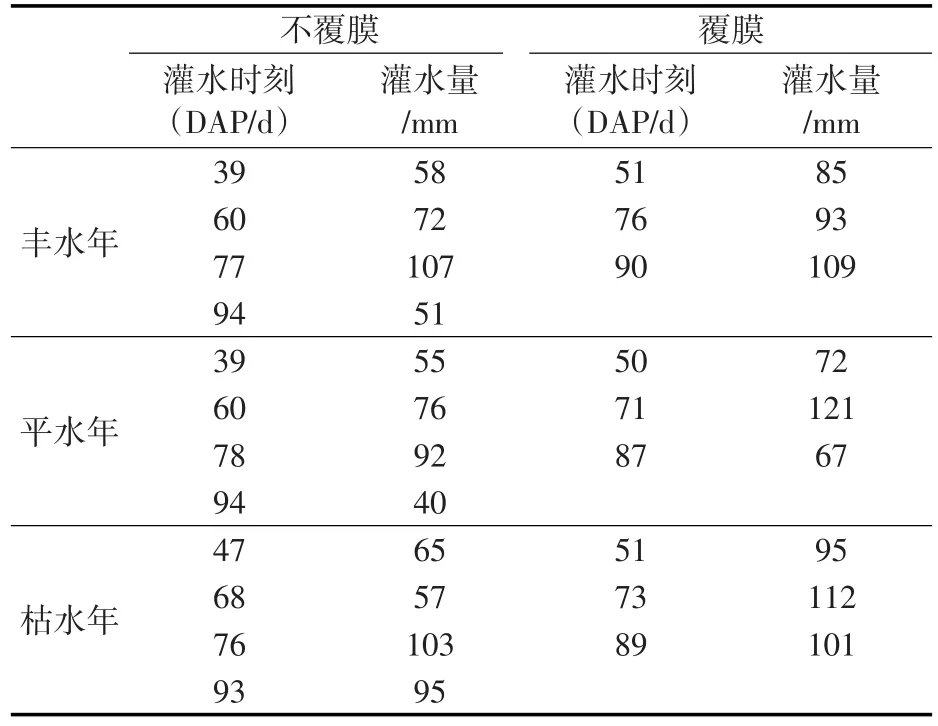
表7 农场决策结果

5 结论

本文基于AquaCrop模型、NSGA-Ⅱ算法以及功效系数法，构建了适用于多种决策依据情况下的灌溉制度多目标优化模型，并以石羊河流域的作物与气象数据为例，求解了不同典型年不同覆膜处理条件下的灌溉制度优化问题。研究结果显示：（1）灌溉制度优化后的水分生产函数呈现出二次函数的形式；（2）覆膜具有增产效应，但增产效应随着灌水量的增加而逐渐减小；（3）不覆膜时灌水次数对产量影响较大，灌水量较小时灌水次数越少产量越高，灌水量大时则相反；（4）本模型较好地满足了不同决策者的决策需求，既可以为以更多经济效益为目标的农场提供决策依据，也适用于以满足口粮为目标的农户，一定程度上可以预测生产者的行为。