基于Monte Carlo方法的地表水地下水耦合模拟模型不确定分析

张将伟，卢文喜，曲延光 ，安永凯

（1.吉林大学 地下水资源与环境教育部重点实验室，吉林 长春 130021；2.吉林大学 环境与资源学院，吉林 长春 130021；3.吉林省水文水资源局，吉林 长春 130021）

1 研究背景

地表水与地下水之间的相互转换是水循环过程中的重要特征［1］，运用数学模型对地表水地下水进行耦合模拟是研究地表水地下水相互作用的常用手段。由于模型输入、模型结构以及观测数据等多个方面存在不确定性，耦合模型的计算结果与真实值之间往往存在一定偏差，这是耦合模型中不确定性的实际体现［2-5］。单纯运用确定性模型研究地表水与地下水的运动与转化规律，只能得到唯一结果，难以确定其可靠程度。对地表水地下水耦合模拟模型进行不确定性分析，可以分析模型的可靠程度，满足管理者对于模型极端情况预测的需求［6］，对地表水地下水联合调度有重要意义。

模型参数的不确定性是模型不确定性研究的重要内容之一［7］。目前，国内外学者在数学模拟模型的参数不确定性分析方面开展了大量工作。在水文模型方面，Beven等人提出水文模型的异参同效性，并发展了GLUE方法（generalized likelihood uncertainty estimation），对水文模型的参数不确定性进行估计［8-10］。在地下水模型方面，按照求解原理可以将不确定性分析方法分为：蒙特卡罗法、矩方程法和贝叶斯法三大类以及其它方法（如条件模拟、敏感度分析、一次二阶矩法等）［11］。Hassan等［12］应用马尔科夫链-蒙特卡洛方法（Markov Chain Monte Carlo，MCMC）对Alaska，Amchitka Island的Milrow试验场的地下水模型参数进行了不确定性评价，证明了MCMC方法能够有效的探索参数分布空间的高概率密度区域，并将其反馈到参数后验概率分布的构造过程；姚磊华等［13］在矩方程法基础上，将Taylor展开、摄动技术、待定系数法和有限元法相结合，提出了待定系数摄动随机有限元法，推导出地下水水头均值和方差的表达式，并选取二维承压地下水水流进行随机模拟；梁婕等［14］应用贝叶斯推断方法和随机模拟技术，定量研究了渗透系数的非均质性对地下水溶质运移的影响，并进行了二维理想算例的分析计算。但以往的研究只局限于地表水或地下水，针对流域尺度的地表水地下水耦合模型进行不确定分析还是有待解决的问题。

本文以石头口门水库上游饮马河汇水流域为例，运用Monte Carlo方法对地表水地下水耦合模拟模型进行不确定性分析。首先，根据研究区地表水地下水的实际条件建立地表水地下水耦合模拟模型，用以描述地表水地下水各自的运动特征及二者之间的水力联系和相互转换作用。运用HGS软件对耦合模型进行求解，并根据实测数据对耦合模型进行校正和检验。应用局部灵敏度分析方法对地表水地下水耦合模拟模型参数进行灵敏度分析，筛选出对模型输出结果影响显著的参数。将灵敏度较高的参数作为随机变量，进行随机试验，对地表水地下水耦合模拟模型进行不确定性分析，考察参数的不确定性对模型输出结果的影响。为减小不确定性分析过程中的计算负荷，应用Kriging方法，建立了地表水地下水耦合模拟模型的替代模型。最后，根据不确定性分析结果，对研究区地表水和地下水生态恶化风险进行风险评估。

2 研究区概况

研究区位于吉林省中部长春市西侧，为石头口门上游饮马河汇水流域，总面积约为1197 km2，如图1所示。研究区地势总体上呈南高北低，全区的平均海拔为418 m。石头口门上游饮马河汇水流域属于温带大陆性季风性气候类型，四季气候变化明显，多年平均降水量642.9 mm，多年平均蒸发量1339 mm。研究区内主要河流为饮马河，由南至北流动，最终汇入石头口门水库。该河段河道较弯曲，河槽宽浅，两岸为平缓的低丘和台地，中下游多为洼地和沼泽，河岸两侧多为砂土和砂壤土，河床内沉积物为砂或者细砂，多年平均径流量约为3 m3/s。

研究区北部为山前平原区，地层岩性以第四系冲积洪积层粗砂和砂砾石为主。南部和西北部为低山丘陵区，地层岩性主要为二叠系拉溪组的浅变质岩和侏罗系上统沙河子组和营城组碎屑岩。中部为波状台地与丘陵状台地区，地层岩性主要为为下更新统白土山组砂砾石、中更新统黄土状亚黏土。区内人工开采地下水主要用于生活用水和农田灌溉，开采量约为1.3亿m3/a。

图1 研究区概况图

3 研究方法

3.1 HydrogeosphereHydroGeoSphere（HGS）是一款由Aquanty公司开发的地表水地下水耦合模拟软件。它从水文循环物理过程出发，充分考虑地表水地下水之间水力联系和相互转化过程，是一款能够在流域尺度下进行地表水地下水耦合模拟的软件。

根据研究区实际情况对研究区地表水系统和地下水系统进行概化。将研究区地表水系统的上游入流断面概化为已知流量边界，研究区下游为石头口门水库，故将下游断面概化为临界深度边界，将汇水流域分水岭概化为零深坡度边界。区内源项主要包括大气降水，汇项主要包括蒸发蒸腾。不同的土地利用类型导致不同的下垫面条件，因此，根据不同土地利用类型将研究区分为耕地、林地、草地、滩地、居民点和城镇六个类别，赋予不同的地表水水力参数，如图2所示。

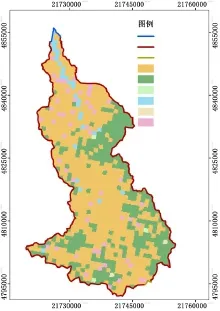
图2 研究区地表水边界与土地利用类型

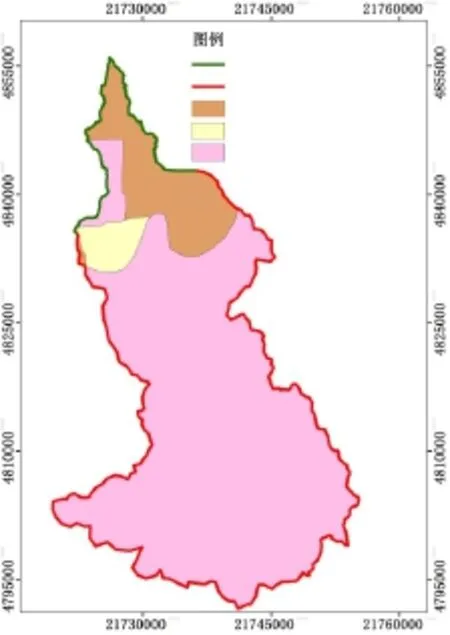
图3 研究区地下水边界与参数分区

研究区地下水系统顶部边界为地表面，与农业灌溉回归水和城镇、农村生活用水回渗等存在水力联系（大气降水补给仅在地表水模型中给予考虑，在地下水模型中不再重复计算。）。研究区底部为透水性较差的淤泥质亚黏土，作为隔水边界。研究区侧向边界如图3所示。研究区北部为山前平原区，地层岩性主要粗砂和砂砾石，大部分区域介质透水性较好，富水性较强；南部低山丘陵区，地层岩性主要为碎屑岩、变质岩和花岗岩，发育在其中的网状裂隙部分被填充，连通性差，地下水富水性较弱；中部为波状台地与丘陵状台地区，地层岩性主要为砂砾石和黄土状亚黏土，地下水富水性较弱。

根据概化结果建立数学模拟模型，见式（1），使用二维Saint Venant方程来描述地表水运动，使用三维Richard方程描述地下水水流运动，使用达西定律描述地表水与地下水交换过程，并在达西定律的基础上引入相对渗透率，反映包气带对地表水地下水水量交换的影响。

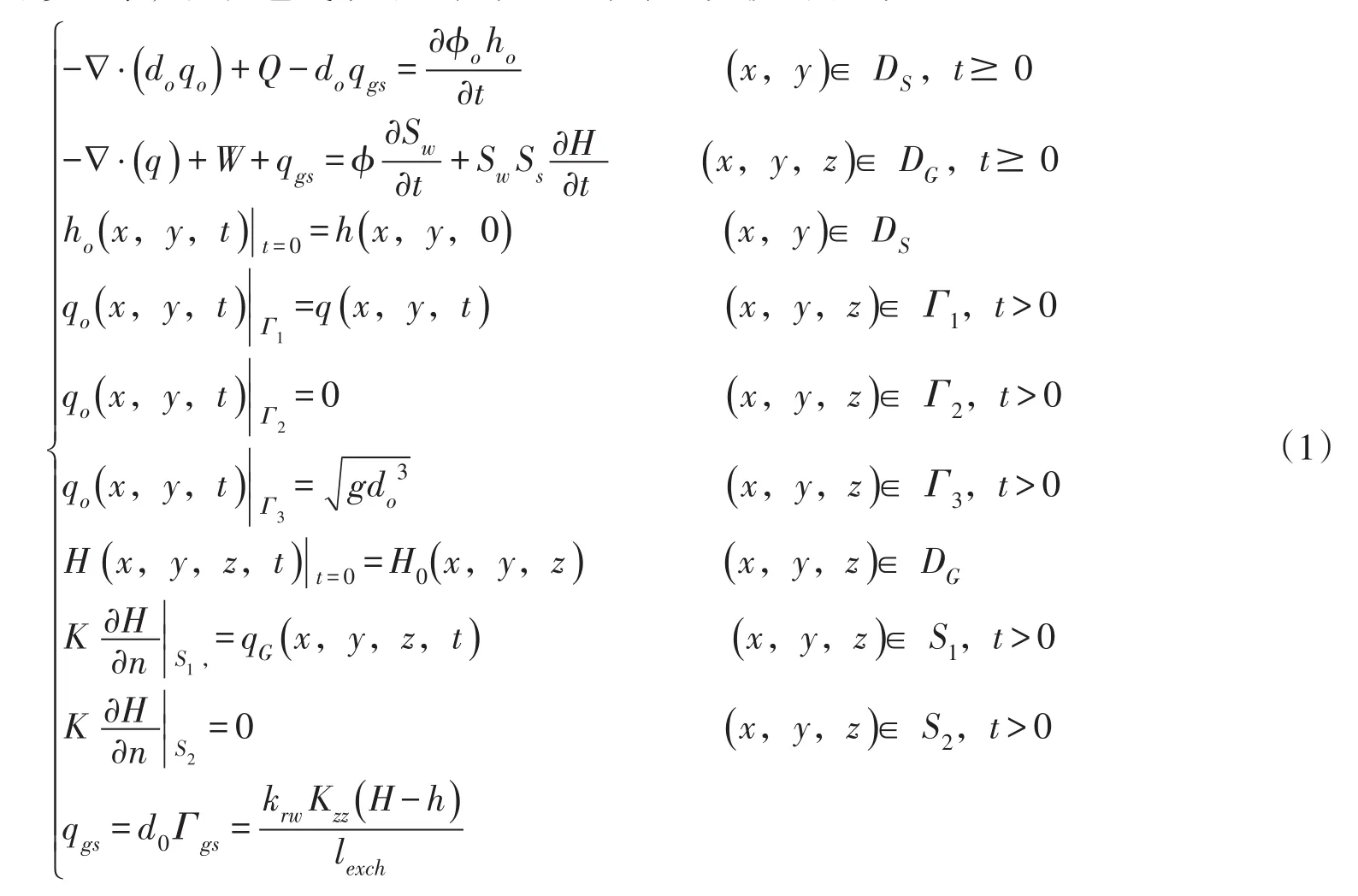
式中：do为地表径流深度，m；qo为地表水流速，m/s；qgs为地下水和地表水之间单位体积流量，s-1；ho为地表水水位，m；Q为地表水的源汇项，为单位面积体积流量，m/s；φo为等效地表孔隙度；h（x，y，0）为（x，y）点初始水位，m；Γ1为上游段面，Γ2为分水岭，Γ3为下游断面；H为地下水水头，m；W为地下水的源汇项，为单位体积流量，s-1；φ为孔隙度，无量纲；Sw为饱和度，无量纲；Ss为储水系数，m-1；qG为边界上的水流通量，m/s；H0为地下水初始水头，m；S1已知流量边界，S2为隔水边界；Γgs为地表水与地下水之间交换通量，s-1；Kzz为含水介质渗透系数，m/s；krw为相对渗透率，无量纲；lexch为地表水与地下水之间的耦合长度，m。

通过Van Genuchten关系来描述相对渗透率（krw）与饱和度（Sw）和压力水头（ψ）之间的关系，其关系式如下：

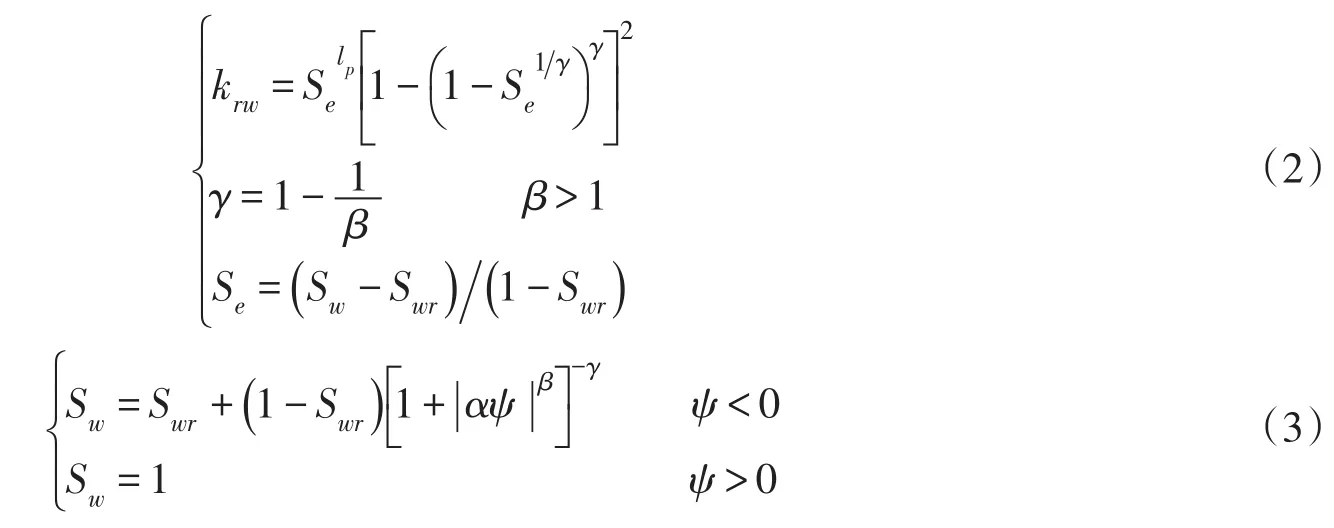
式中：lp为孔隙连接指数；γ为经验参数；Se为有效含水量；Swr为残余含水率；α、β为VG方程参数。

在平面上，采用三角网格剖分法对模型进行剖分，共得到节点5539个，三角形单元10448个。在垂向上，根据地层岩性，将含水层剖分为10层，弱透水层剖分为1层。同时，为研究地表水与地下水的相互作用，在地下水地表水交界面附近进行加密剖分，模型空间离散图如图4所示。

图4 模型空间离散示意图

基于研究区已有的水文及水文地质资料，选取2016年7月25日作为初始时刻，使用观测资料插值获得研究区地下水初始水位和地表水初始水深，非饱和带水分分布可由式（2）、式（3）计算得出。将2016年7月25日—8月25日作为模型的校正时段，校正期内逐月观测数据作为校正依据，采用试估校正法来校正模型各参数和源汇项。在此基础上将2016年8月26日—9月26日作为模型的检验时段，检验期内逐月观测数据作为检验依据。

3.2 灵敏度分析灵敏度分析可以定量地评价输入参数变化对输出结果的影响，通过确定模型中灵敏度较高参数可以减少Monte Carlo模拟所考察的参数个数，从而简单、高效地对模型进行不确定性分析。按分析方法分类，灵敏度可以分为局部灵敏度分析和全局灵敏度分析［15-17］。由于全局灵敏度分析时需要多次调用模拟模型，耗费时间较长，尤其是本次研究过程中所建立的地表水地下水耦合模拟模型采用牛顿迭代方法求解，在保证研究结果精度的前提下，运行时间较长。因此本文采用局部灵敏度分析方法对模拟模型参数进行灵敏度分析。

从数学意义上来讲，参数灵敏度可理解为变量x的微小变化所引起的函数F（x）的变化程度。局部灵敏度计算公式如式（4）所示：

式中：S为参数灵敏度；xi代表不同的模型参数；Δxi代表对参数xi的微小扰动。

3.3 Monte Carlo方法Monte Carlo方法是一种随机分析方法，它是一种通过随机实验来求解随机问题的技术，即采用统计抽样理论近似求解数学问题或物理问题的一种方法，是进行不确定性分析的一种有效方法［18-21］。

蒙特卡罗模拟方法假定随机变量的概率分布函数已知，通过随机抽样方法获得多组输入变量，每组变量都相当于一次统计试验，然后将随机变量带入模型中从而得到大量的输出，根据对输出结果的统计可以得到均值、方差等统计估计量，并拟合其输出结果的概率分布情况。

它的主要思路如下：（1）在各随机变量的可行域内根据其服从的概率分布进行随机抽样。在抽样过程中，可以采用拉丁超立方抽样法，使得样本的覆盖率更高，减少抽样次数。（2）将随机变量的抽样结果进行随机组合后，通过运转模型获得相应的输出结果。（3）统计分析模型输出结果，根据统计结果的均值、方差等估计量，拟合输出结果的概率分布情况，定量描述模型的不确定性。

为了减小Monte Carlo方法应用过程中反复调用耦合模拟模型所导致的大量计算负荷，本文应用Kriging方法建立耦合模拟模型的替代模型。

3.4 Kriging方法Kriging方法是建立在变异函数理论分析基础上，对有限区域内的区域化变量取值进行无偏最优估计的一种空间局部内插法。近年来，被广泛应用于建立替代模型［22-25］。Kriging模型表达式如下：

式中：f（x）=［f1（x），f2（x），…，fk（x）］为已知回归模型的基函数；β=［β1，β2，…，βk］为待定参数；z（x）为随机部分，均值为0，方差为σ2，协方差为：

式中R（xi，xj）为点和点的关联系数，可用高斯模型进行计算：

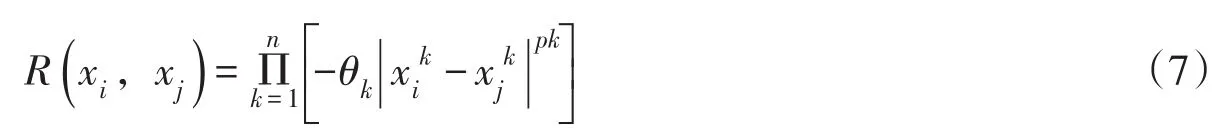
式中：n为设计变量个数；θk和pk为待定系数。则有已知在点x处的y（x）估计值为：

式中：rT（x）为点x与m个采样点之间的相关向量；y为m×1向量，包含m个采样点对应的响应值；β可由最优线性无偏估计得到：

式中R为n个采样点相关系数组成的相关矩阵：

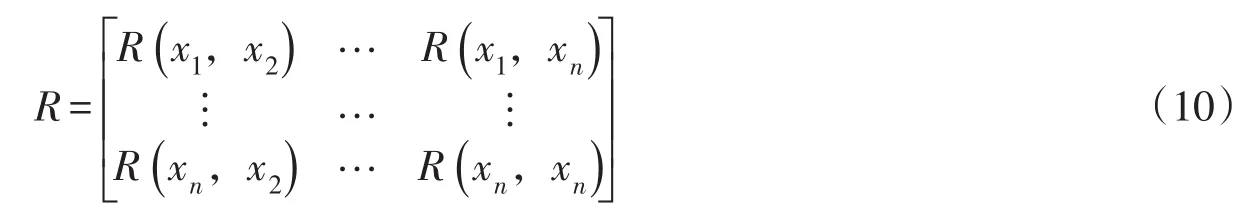
方差σ2的估计值可用σ2=（y-fβ）TR-1（y-fβ），参数θk则根据极大似然估计给出［26］。

4 结果与讨论

4.1 模型的校正与检验结果地表水地下水耦合模拟模型校正和检验末刻，各观测井地下水水头的实测值与计算值如图5所示，各测站地表径流量的实测值与计算值如表1所示。

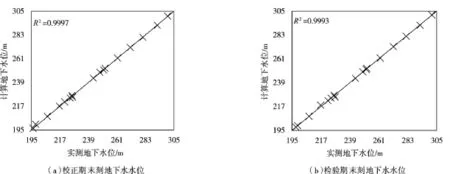
图5 地下水观测井实测水位与计算水位

表1 地表水测站实测流量与计算流量

由图5可知，校正和检验阶段地表水地下水耦合模拟模型中地下水水位的计算值、实测值与y=x间的拟合度分别为0.9997和0.9993。

使用相对误差和NSE（纳什效率系数）误差评价地表水流量的校正检验的精度。NSE误差计算方法如下：

式中：T为地表水测站数量；Qo为地表水流量的实测值；Qm为计算值。

由表1可知，各测站地表径流量的计算值与实测值的相对误差均小于20%，且NSE误差均大于0。

综上所述，所建立的地表水地下水耦合模拟模型能够反映研究区的地下水水位变化和地表水流量变化的实际情况。研究区水文地质参数和地表水力参数的取值如表2、表3所示。

4.2 灵敏度分析结果根据研究区水文地质参数分区，选取井5、井13、井14（图1）作为不同水文地质区域的典型研究对象，地表水测站选取小金屯测站为研究对象。

对地表水地下水耦合模拟模型中的渗透系数、孔隙度、弹性释水系数、曼宁系数洼地储存量和耦合长度进行局部灵敏度分析，分析结果如图6所示。由图6可知对耦合模拟模型中地下水水位影响较大的2个随机参数分别是渗透系数和孔隙度，对耦合模拟模型中地表径流量影响较大的2个随机参数分别是渗透系数和曼宁粗糙系数，渗透系数的变化不仅对会耦合模型中地下水水位影响较大，也对地表径流量影响较大。

表2 研究区含水层水文地质参数校正结果

表3 研究区地表水水力参数校正结果

图6 典型观测井与测站灵敏度分析结果

故将渗透系数、孔隙度和曼宁粗糙系数作为随机变量，其他参数取校正值作为确定值输入模型。4.3 Kriging模型将预报期设为2016年10月31日，利用地表水地下水耦合模拟模型进行预报。根据灵敏度分析结果，将曼宁粗糙系数、孔隙度和渗透系数作为随机变量，其取值范围为校正值±20%，其他参数及源汇项设定为校正值。根据前人经验，曼宁粗糙系数、孔隙度和渗透系数服从的参数分布如表4所示。

运用拉丁超立方方法抽样100组随机变量，作为100组预报方案。统计100组预报方案下地表水地下水耦合模拟模型中井5、井13、井14与小金屯测站的预报结果，以此为基础建立Kriging替代模型代替耦合模拟模型。

运用MATLAB软件建立替代模型。将耦合模拟模型的100组预报结果中前90组作为替代模型的训练样本来训练替代模型。后10组作为替代模型的检验样本，来检验替代模型的拟合精度，检验结果见图7。

由图7可知，替代模型的地下水水头输出结果与耦合模拟模型地下水水头的变化趋势基本一致，且相对误差均小于0.2%；替代模型的地表径流量输出结果与耦合模拟模型地表径流量的变化趋势基本一致，相对误差小于4%。拟合相对误差较小，说明替代模型精度较高，可以代替耦合模拟模型求解。

4.4 不确定性分析再次利用拉丁超立方方法抽取1000组随机变量样本，作为输入数据集。将输入数据集输入Kriging替代模型，求解得到1000组井5、井13、井14和小金屯测站的输出值。

对所获取的1000组输出值进行统计分析，统计结果如表5所示。由表5可知井14、井5、井13标准差依次变大，说明输出结果越来越分散，不确定性越来越大。这可能与含水介质不同有关，井5、井13、井14分别为碎屑岩-花岗岩含水层、黄土状亚黏土含水层和第四系冲积洪积物含水层地区典型观测井，故认为耦合模拟模型中亚黏土含水层地区输出结果的不确定性大于碎屑岩-花岗岩含水层和第四系冲积洪积物含水层。

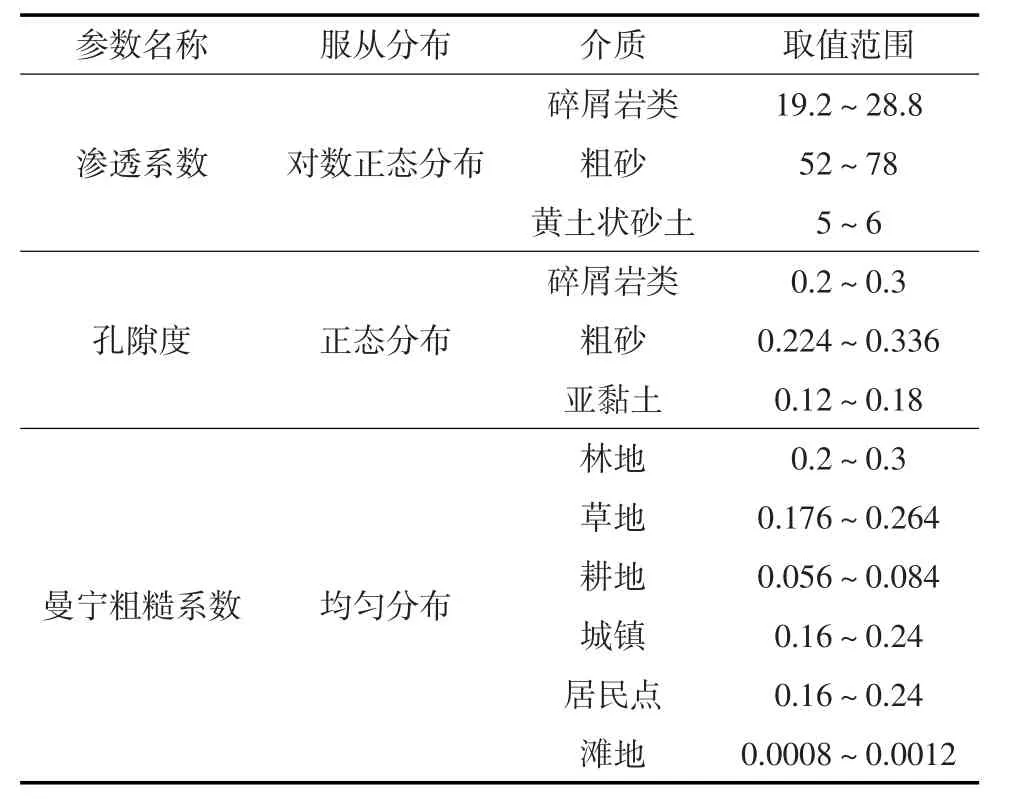
表4 参数的概率分布与取值

图7 替代模型精度检验

假设井5、井13、井14和小金屯测站的输出数值均符合正态分布，利用SPSS软件中的S-K检验分别对各组输出数值进行假设检验。根据前人经验认为当双侧渐进显著性大于等于0.05时假设成立，故小金屯测站输出数值符合均值为11.21、标准差为0.68的正态分布，井5输出数值符合均值为230.77、标准差为0.09的正态分布。井13、井14输出数值分布未知。

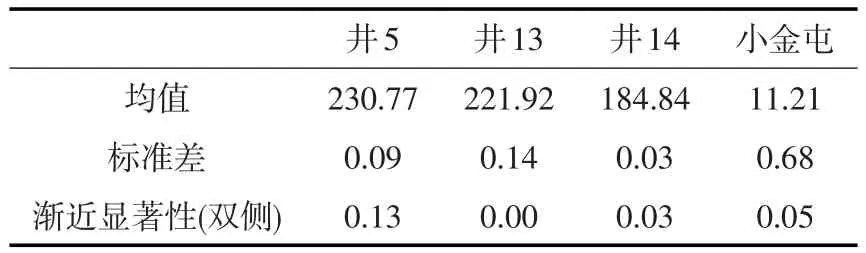
表5 输出数据单样本K-S分析结果

4.5 区间估计区间估计指在概率学中一定置信度下对未知参数真值存在范围的估计。本文将井5、井13、井14和小金屯测站的输出值作为未知参数，计算其在不同置信水平下的区间范围。

切比雪夫不等式适用于分布未知，而已知平均值和方差的情况，故对井13、井14运用切比雪夫不等式进行区间估计。井5、小金屯测站的输出数值均符合正态分布，运用概率密度函数计算。井5、井13、井14和小金屯测站区间估计结果如表6所示，由表可以看出，置信水平越高，区间范围越大；置信水平越低，区间范围越小，也越集中在均值附近。

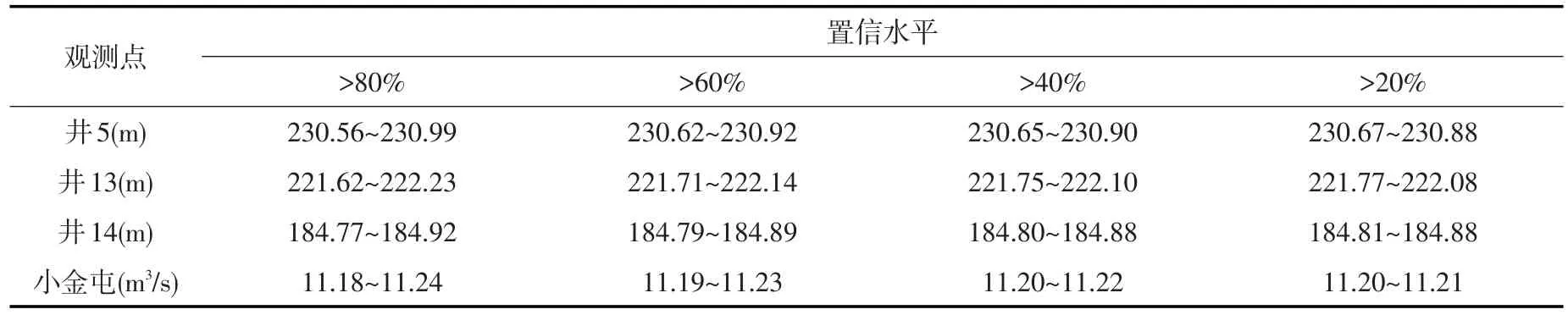
表6 不同置信水平下典型观测井与测站的区间估计

4.6 生态风险评估生态风险评估是描述和评估人为活动、环境污染和自然灾害对生态系统结构与功能产生负面作用的可能性及其大小的过程［27］。通常使用指数法，模拟法和统计法进行生态风险评估。本文采用模拟法，根据统计不确定分析过程中获取的1000组输出结果和地表水流量与地下水水位的生态阈值，对地表水流量与地下水水位变化超出生态阈限的状况进行了风险评估。

根据经验，假设预报期末刻，井5、井13、井14水位同时低于230.65、221.80、184.8 m时存在地下水生态环境恶化风险；小金屯水文站流量小于10.5 m3/s会引起地表水水生态环境恶化。根据各个观测井、水文测站输出值累积分布函数画出风险评估图（图8）可以看出，在当前开采状态下，井5、井13、井14水位低于230.65、221.80、184.8 m分别为11%、6%和12%，故存在地下水生态环境恶化风险概率为6%。同理，在当前开采状态下，地表水生态环境恶化风险为15%。

图8 各观测井和测站风险评估图

4.7 计算负荷分析在CPU为Intel Xeon E5 2.4G Hz，内存为64 GB，操作系统为Windows 7的计算机上，运行一次石头口门水库上游饮马河汇水流域地表水地下水耦合模拟模型需要的时间约为加粗4.7 s（5.5 h），而运行一次替代模型需要的时间约为10 s。说明建立替代模型可以有效减小Monte Carlo过程中反复调用耦合模拟模型所产生的计算负荷。

5 结论

本文以石头口门水库上游饮马河汇水流域为研究区，建立研究区地表水地下水水流耦合数学模拟模型。通过局部灵敏度分析法获取了3个敏感性较大参数作为随机变量。运用Monte Carlo方法对耦合模拟模型进行不确定性分析。

灵敏度分析结果表明，渗透系数，孔隙度和曼宁粗糙系数对地表水地下水耦合模拟模型的输出结果影响较大。其中，渗透系数的变化不仅会对耦合模型中地下水输出结果产生影响，也会通过改变地表水地下水之间的交换量，对地表水的输出结果产生影响。

利用Kriging方法建立的替代模型能够充分逼近地表水地下水耦合模拟模型的输入响应关系。在不确定性分析过程中运用替代模型能够大幅度反复调用耦合模拟模型所产生的计算负荷。

风险评估结果表明，在当前开采状态下，研究区地下水生态环境恶化风险概率为6%，地表水生态环境恶化风险为15%。

运用区间估计方法可以计算不同置信水平下地表水流量和地下水水位的取值区间，相较于确定性模型所得到的唯一结果更有实际指导意义。