中考概率题型梳理
王 磊

同学们,“等可能条件下的概率”是中考中常见的考查内容,其考试题型包含选择、填空和解答题.课标对此部分的要求较为基础,所以题目难度不大,但要能获得全部分数,还是需要十分的仔细和认真.下面让我们通过几个例子,了解一下概率问题在中考中的常见类型.
一、面积问题
例1 (2018·江苏常州)中华文化源远流长.下图是中国古代文化符号的太极图,圆中的黑色部分和白色部分关于圆心中心对称.在圆内随机取一点,则此点取黑色部分的概率是 .

【分析】根据中心对称图形的性质,得到圆中的黑色部分和白色部分面积相等,所以此点取黑色部分和白色部分的概率相等.
【解答】∵圆中的黑色部分和白色部分关于圆心中心对称,
∴圆中的黑色部分和白色部分面积相等,
【点评】本题利用面积估计概率,结合生活中常见的图形,渗透了一定的人文教育价值.掌握中心对称图形的知识,理解概率估测方法是解题的关键.
二、角度问题
例2 (2018·江苏连云港)如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( ).


【分析】指针指向结果有1,2,3,4,5,6共6种情况,其中大于3的情况有4,5,6三种情况,∴P(指针指向大于3的数)=.
【解答】D.
【点评】本题从形式上看,是通过数数字来解决问题,但其背后的原理是:正六边形的每条边对应的中心角都相等,故指针转到每个区域的概率都相等.中考中,这样类型的题目还有很多,例如转盘问题也是利用类似的几何原理设计的.
三、摸球问题
例3 (2018·江苏南京)甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.
(1)求摸出的2个球都是白球的概率.
(2)下列事件中,概率最大的是 .
A.摸出的2个球颜色相同
B.摸出的2个球颜色不相同
C.摸出的2个球中至少有1个红球
D.摸出的2个球中至少有1个白球
【分析】(1)先画出树状图展示所有6种等可能的结果数,再找出2个球都是白球所占的结果数,然后根据概率公式求解.
(2)根据概率公式分别计算出每种情况的概率,然后即可得出答案.
【解答】(1)画树状图如下:

由树状图知,共有6种等可能结果,其中摸出的2个球都是白球的有2种结果,所以摸出的2个球都是白球的概率为.
∴概率最大的是摸出的2个球中至少有1个白球.
故选:D.
【点评】此题主要考查了用列表法与树状图法求概率.列表法可以不重复不遗漏地列出所有可能的结果,适合两步完成的事件;树状图法适用于两步或两步以上完成的事件.解题时还要注意,是放回试验,还是不放回试验.要熟练掌握某一事件发生的概率等于所求情况数与总情况数之比,结果要化为最简分数.
四、综合问题
例4 (2018·内蒙古通辽)为提升学生的艺术素养,学校计划开设4门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对4门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整.

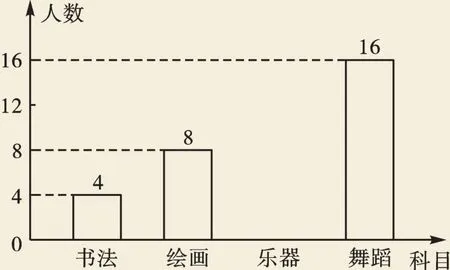
学生选修课程条形统计图
(3)学校为举办2018年度校园文化艺术节,决定从书法(A)、绘画(B)、乐器(C)、舞蹈(D)4项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
【分析】(1)用选A科目人数除以其对应的百分比可得总人数,用360°乘C对应的百分比可得∠α的度数.
(2)用总人数乘C科目对应的百分比即可得出选C科目的人数,从而补全图形.
(3)画树状图展示所有12种等可能的结果数,再找出恰好是“书法”“乐器”的结果数,然后根据概率公式求解.
【解答】(1)本次调查的学生总人数为:4÷10%=40(人),∠α=360°×(1-10%-20%-40%)=108°.
(2)选C科目人数为:40×(1-10%-20%-40%)=12(人),补全图形如下:

学生选修课程条形统计图
(3)画树状图为:

共有12种等可能的结果数,其中恰好是书法与乐器组合在一起的结果数为2,所以书法与乐器组合在一起的概率为
【点评】本题是一道综合类问题,考查内容包括:概率与统计、几何计算、图形绘制等,当然阅读量也比较大,综合性较强,难度较大,也是近些年中考中常见的考查形式.同学们在解决这类问题的时候,一定要耐心和细致.

