带端封挤压油膜阻尼器减振特性分析及试验

，，，

(中国航发商用航空发动机有限责任公司，上海 200241)

近几十年来，随着对航空发动机高性能、高可靠性的要求，发动机转子越来越倾向于设计为重量轻、转速高，因此带弹性-挤压油膜阻尼器被广泛应用于转子的支承设计，使得转子平稳顺利地通过一阶或二阶临界转速，极大地提高了转子系统的安全性[2]。

航空发动机作为飞机的“心脏”，在航空技术的发展过程中起着关键性作用[2]。航空发动机的整机振动将对发动机的研制和寿命等产生直接的影响[3]，而转子—支承系统的振动和稳定性常常是问题的症结。因此，对转子-支承结构动力特性进行研究和优化以减小发动机整机振动不失为行之有效的方法[4]。挤压油膜阻尼器通常置于滚动轴承与支承结构之间，以减少外传振动负荷与振幅，降低发动机的整机振动的水平。因此，研究并掌握挤压油膜阻尼器动力特性，成为改善航空发动机整机振动问题重要而有效的途径。

40多年来， SFD减振技术(如图1)已广泛应用于高转速的涡轮机械，并经过持续研究已经发展出一套方法，通过优化SFD设计参数以满足整机动力学设计，如Zeidan等人的文献[5]。文献[6-7]通过试验及理论研究阻尼器特性，且主要以流体惯性效应、滑油的气穴现象以及边界条件(例如供油系统和端部密封)等，对阻尼特性的影响进行了系统研究。

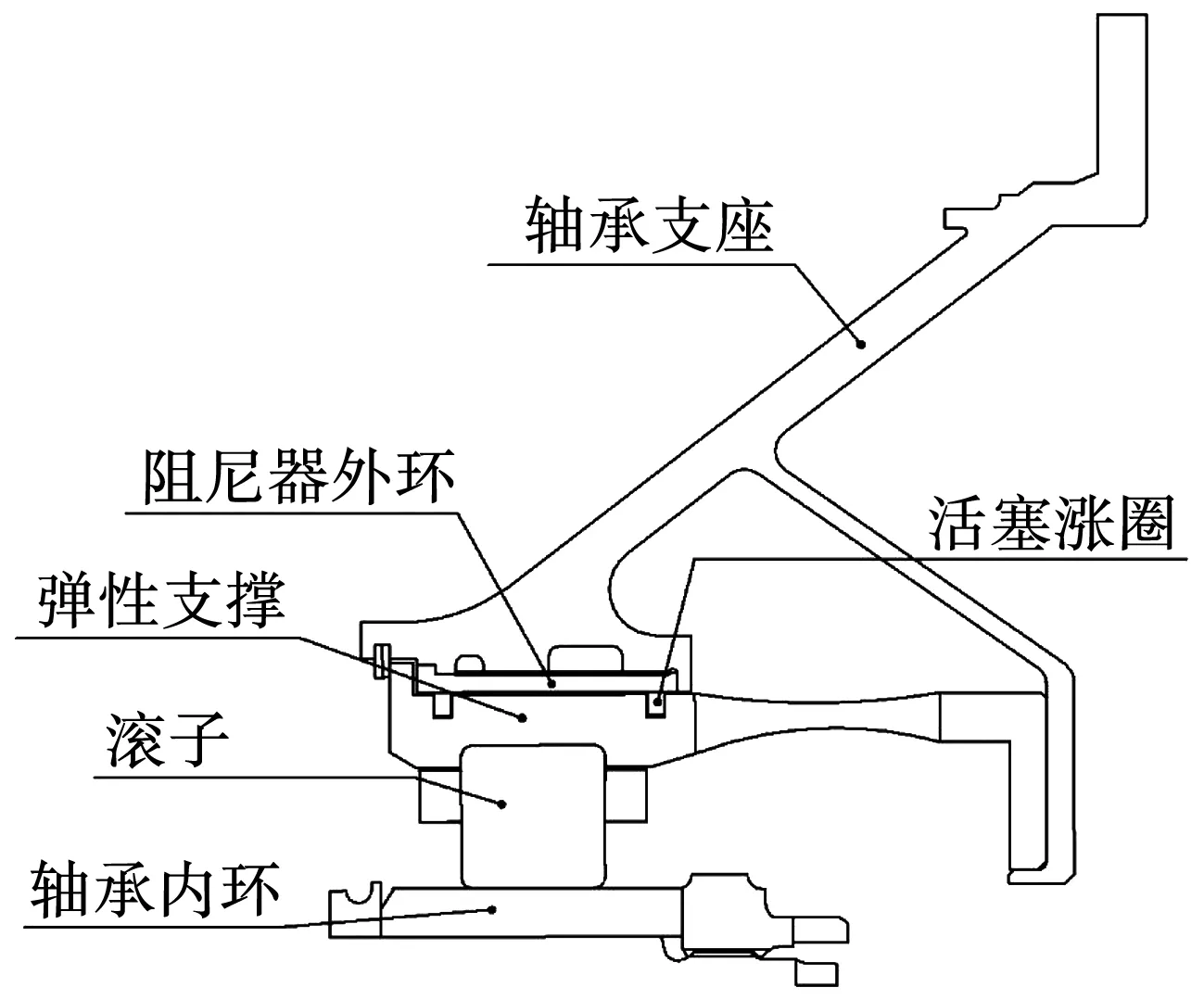
图1 带弹支定心的挤压油膜阻尼器示意图

基于SFD的工作机理及润滑原理，Zeidan和Vance[8]认为存在四种状态的气穴：润滑油中自然存在的空气空穴、气液两相现象、汽化空穴、气相结合汽化空穴。目前，Gumbel和Swift[9]假设是SFD气穴模型中最常用的，但是，这种计算模型不符合质量守恒原则。Diaz和 San Andrés[10]基于质量守恒，假定油膜中存在一定量的气体与滑油均匀地混合，并采用可压缩介质的Reynolds方程，且在体积微元中密度和粘度皆为气体和滑油混合比的函数，以求解油膜压力分布。SFD动特性的计算分析表明：当雷诺数Re=ρωC2/μ大于1时[11]，流体的惯性效应将非常显著，且可采用动量法或能量法等计算SFD的惯性效应。Duarte[12]等采用动量法，在雷诺方程中增加了加速度项，并明确了油膜反力由粘性力和惯性力产生，计算了短轴承SFD的动特性。El-Shafei[13-14]采用能量法分析了SFD的动特性，并将粘性项独立于惯性项，且惯性项由拉格朗日方程和雷诺运输定律确定。

SFD的供油方式一般可采用油孔供油或周向油槽供油，试验表明供油方式对SFD工作有重要影响[15-17]，而从计算的角度，不同的供油方式需采用不同的油膜边界条件。通常对于周向油槽的供油方式，一般假定油槽部分的油压为常数，但是，San Andrés证实油槽的油压并非如传统假设，油槽油压呈一定的分布并会影响油膜阻尼器的性能，且其假设及计算模型通过试验得到了验证[18-20]。相比于油槽供油，油孔供油增加了油膜有效承载面积能增加阻尼器的阻尼能力[21-22]。目前，只有少量文献研究油孔供油的挤压油膜阻尼器。Marmol和Vance[23]基于雷诺方程，并在油孔处增加了质量平衡方程，采用数值方法进行了计算分析。Assis Rodrigues[24]的分析模型中不仅仅考虑了SFD，还将整个供油系统的影响都包括在内，进行了详尽的计算分析。

SFD通常采用端部密封设计，减少两端泄漏量以增加阻尼能力[25]。最常用的端封结构包括：O型胶圈、活塞涨圈、端部平板密封。油膜端部完全密封能增加阻尼能力，但也会导致油膜温度上升，因此，必须设计合理的泄漏量，例如通过设计开口的活塞涨圈以满足泄漏要求。Marmol和Vance[23]建议在计算模型中，端部密封处引入压降或引入泄漏系数来控制端部泄漏量。

本文采用有限差分法建立了SFD的求解模型，采用求解模型对San Andrés文献中提供的带试验结果的两种结构的SFD进行了阻尼特性分析，仿真分析结果与试验结果基本一致；并新设计了SFD结构及转子试验器，求解了SFD的阻尼值并进行了转子稳态不平衡响应分析，通过试验和仿真分析研究并验证了SFD减振效果和计算模型。

1 挤压油膜阻尼器计算模型

本文基于Reynolds方程，求解挤压油膜阻尼器的压力分布特性，由于油膜在工作过程中只受到挤压效应，因此，纯挤压效应下的Reynolds方程

(1)

式中R——SFD轴颈半径;

θ——周向角坐标;

h——油膜厚度;

μ——滑油动力学粘度;

P——油膜压力;

z——轴向坐标;

t——时间。

上式是基于层流假设，且未考虑流体惯性效应，当Re=ρωC2/μ<1时，采用上述方程式满足计算要求的。

如图2所示，沿周向的油膜厚度h可表示为

h(θ,t)=C-x(t)cosθ-y(t)sinθ

(2)

当油膜阻尼器轴颈为圆进动时，可得如下方程

x(t)=e*cos(ωt),y=e*sin(ωt)

(3)

式中e——油膜动态偏心量;

ω——转子进度角速度。

图2 挤压油膜阻尼器坐标示意图

SFD阻尼采用传统定义方法

C0=Ft/(e×ω)

(4)

式中C0——等效阻尼;

Ft——切向力。

本文采用有限差分法和超松弛迭代法求解Reynolds方程，且油膜破裂边界采用Reynolds边界条件。

本文挤压油膜阻尼器的端部密封采用活塞涨圈的密封形式，依据文献[23]对这类端封模型的处理可采用式(5)的表达式。泄漏系数Cl为常数，用来模拟端部泄漏量，式中zend为SFD两端部坐标，P0为挤压油膜阻尼器两端的环境压力

qz(θ,zend)=Cl×[P(θ,zend)-P0]

(5)

依据San Andrés的研究文献[18-20]，计算模型不能简单地将油槽处的油膜压力设定为供油压力；试验表明油槽处的滑油压力与油膜处的滑油压力量级相当，且略小于油膜处的滑油压力；因此，本文的计算模型中，考虑了油槽压力分布对SFD阻尼特性的影响。

2 计算模型验证

本文以文献[1]中提供的相似结构SFD的试验结果为参考，对SFD计算模型进行验证，对比分析结果见表1；由表1可知，仿真分析结果与试验测试结果基本一致，因此，计算模型的仿真结果具有较高的可信度。

表1计算模型验证分析

结构类型结构A结构B阻尼器直径/mm127127油膜间隙/mm0.1410.138阻尼器总长度/mm63.538.1油槽宽度/mm12.712.7油槽深度/mm9.59.5阻尼器有效长度/mm50.825.4滑油粘度/Pa·s0.002 960.002 96泄漏系数Cl/ m2·(Pa·s)-16.25×10-115.83×10-10偏心率0.060.06试验结果/N·s·mm-153.8～60.412.7～13.8仿真结果/N·s·mm-157.713.5

3 挤压油膜阻尼器-转子试验装置

图3展示了试验件转轴结构、支承结构和主要测量参数。转轴由前后两个轴承进行支承，且前轴承通过弹支连接到刚性支承座，后轴承直接与刚性支承座相连。转轴最右端采用柔性联轴器与驱动电机相连，作为试验件的动力输入端。前、后设计了两个平衡面，作为转轴动平衡的配平面。试验过程中，分别采用弹支应变计和加速度计对弹性支承的应变和前支承座的振动加速度进行测量，以记录试验过程中的弹支应变和前支承座的振动响应。

图3 试验件及测量参数示意图

图4为试验件前支点的SFD结构示意图，SFD通过弹支定心安装到前支承座。SFD两端采用活塞涨圈进行密封；供油方式采用周向油槽供油，且油槽位于SFD左端靠近活塞涨圈位置，试验过程中通过流量计和压力计，以记录供油流量和供油压力。SFD供油温度可由油温控制单元，将供油温度控制在65℃，以便将滑油粘度控制在要求范围内。

图4 阻尼器局部示意图

SFD及试验件的详细参数详见表2。通过有限元分析，转轴在不带阻尼情况下的一阶临界转速(刚体型)为5 500 rpm，二阶临界转速(弯曲型)为21 000 rpm。整个试验最高转速可推转至12 000 rpm，通过监测试验件过一阶临界的弹支应变及振动响应，来验证SFD的阻尼减振效果。

表2挤压油膜阻尼器参数表

阻尼器直径/mm160 油膜半径间隙/mm0.15阻尼器总长度(两涨圈之间)/mm29.1油槽宽度/mm2.5油槽深度/mm4阻尼器有效长度(去除油槽宽度)/mm25.3供油孔尺寸/mm4滑油粘度(65℃)/Pa·s0.012弹支刚度/N·m-12.8×107转轴总质量/kg178 转轴跨距(两轴承之间)/mm1 188

4 试验结果及分析

4.1 SFD阻尼特性分析

依据表2的SFD设计参数，通过试验过程中，记录SFD的滑油泄漏量为0.7 L/min，由公式(5)计算可得泄漏系数Cl为4.67×10-11m2/Pa·s，考虑到泄漏量测量本身存在误差，计算SFD的阻尼特性时，考虑±20%的泄漏量误差，具体计算结果详见表3。由计算结果可知，由于SFD端部采用活塞涨圈起到了较好地密封效果，泄漏量在小范围内变化对SFD阻尼特性影响较小。

表3 SFD的阻尼特性计算表

泄漏系数Cl/ Pa·s3.74×10-114.67×10-115.6×10-11阻尼计算值/mm187 N·s/mm183 N·s/mm181 N·s/mm

4.2 SFD减振特性分析

本文采用通用有限元软件Samcef for rotor进行转子动力学稳态不平衡响应分析，前后平衡面分别加载同相位的1 300 g·mm(10倍G2.5)的不平衡量，前支点的阻尼值分别取表3和无SFD阻尼的四种情况进行对比分析，分析结果见图5和图6。由图可知，表3的三种阻尼情况下，振动响应变化很小，其影响基本可忽略不计；由于SFD阻尼的存在，会改变振动响应的峰值转速，无阻尼情况下的一阶振动峰值为5 500 rpm，而存在较大SFD阻尼时的一阶振动峰值则为7 200 rpm；对比存在SFD阻尼和无SFD阻尼的振动响应，前支点反力和前支点位移减振效果皆大于60%，尤其是前支点位移的减振效果大于90%；采用半功率带宽法求得带SFD阻尼时，一阶临界响应的阻尼比ζ为8%。

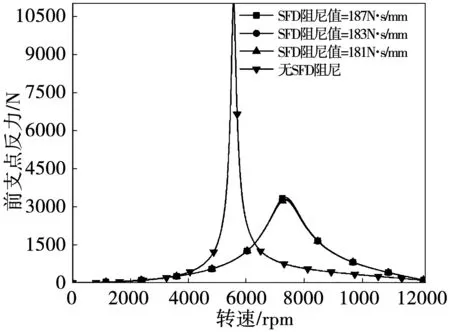
图5 不同阻尼下的前支点反力

图6 不同阻尼下的前支点位移

4.3 试验结果对比分析

试验过程中，分别对前支点弹支应变和前支座的振动加速度进行了测量。由于支反力传递到支承座引起支座振动，因此，在线性范围内，前支座振动加速度和前支点反力为线性关系；弹性支承为柔性支承结构，在弹性范围内，弹支应变与与前支点位移也为线性关系。

本文将试验中测得前支点振动与前支点反力、弹支应变与前支点位移的基频量进行了对比分析，结果如图7和图8；由于试验过程中转轴实际的不平衡载荷难以有效监测，因此，试验结果与仿真结果的对比仅限于峰值转速及阻尼效果(阻尼比)。从试验结果可知，支座振动加速度一阶响应峰值小于0.5 g，弹支应变一阶响应峰值小于40 με；支点振动加速度与支点反力的峰值转速基本一致，误差小于3%，弹支应变与支点位移的峰值转速略有差异，但误差小于5%，由此可知，带SFD阻尼的转子-支承系统响应的试验和仿真结果基本一致。采用半功率带宽法，分半计算了试验各振动响应的阻尼比ζ，具体结果见表4。由表可知，除去前支座水平振动加速度的阻尼比ζ=6.34%小于8%的仿真值，其余各测点试验结果与仿真结果基本一致，由此可知，仿真的SFD阻尼值与试验结果基本一致(阻尼比ζ差异小于0.7%)，从而验证了SFD仿真结果的合理性。

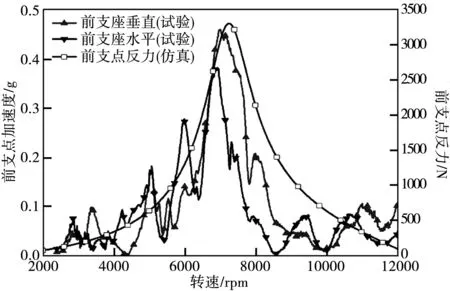
图7 支座振动与支点反力对比

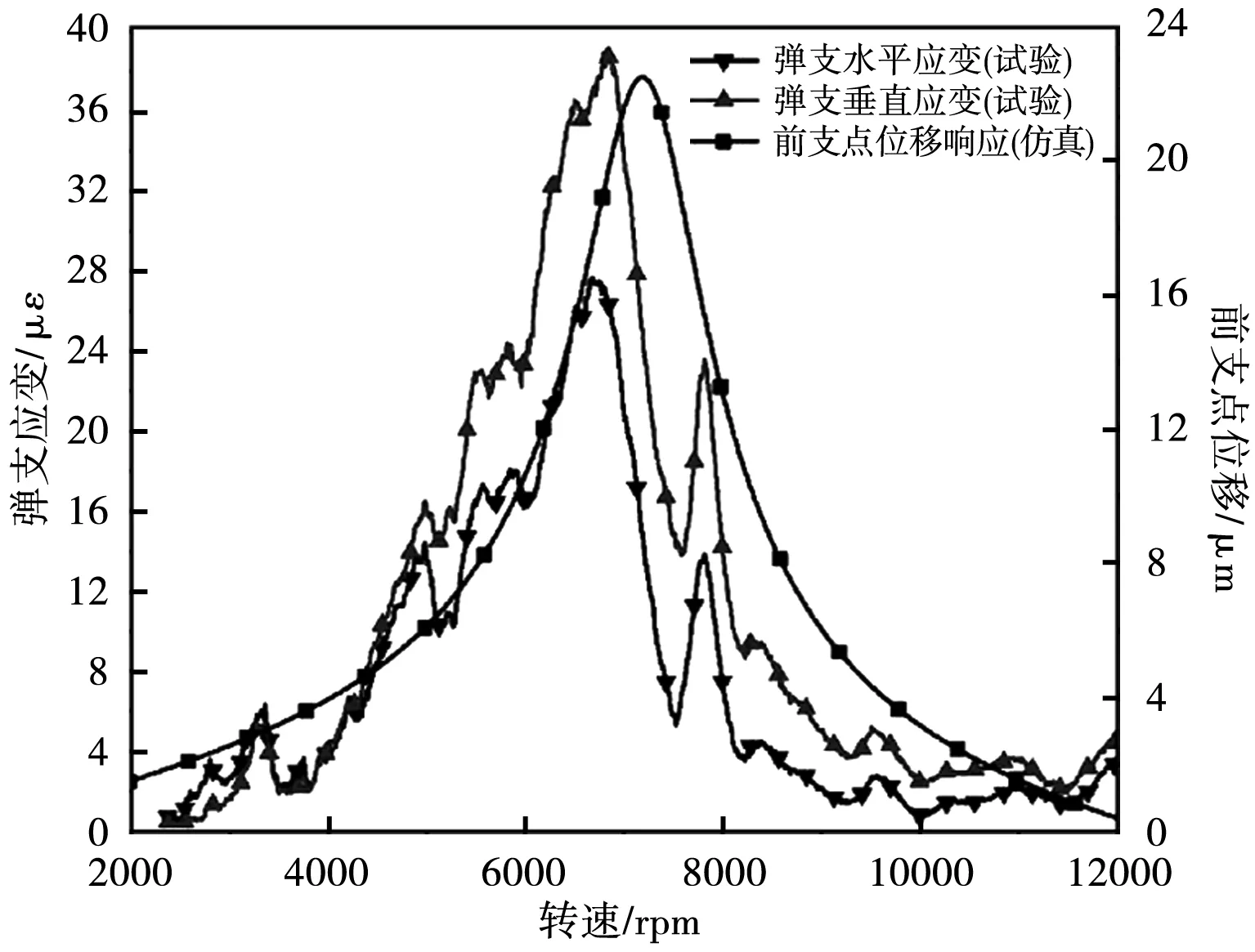
图8 弹支应变与支点位移对比

表4各响应阻尼比

振动响应参数阻尼比ζ/[%]前支点反力8前支座垂直振动加速度7.3前支座水平振动加速度6.4前支点位移8弹支垂直应变7.5弹支水平应变7.3

5 结论

基于雷诺方程，本文采用有限差分法建立了SFD求解模型，采用求解模型对San Andrés文献中提供带试验结果的两种结构的SFD进行了阻尼特性分析，仿真分析结果与试验结果基本一致；并设计了SFD结构及转子试验器，求解了SFD的阻尼值并进行了转子稳态不平衡响应分析，通过试验和仿真分析研究并验证了SFD减振效果，得到结论如下：

(1)通过文献结果及试验结果，验证了SFD计算模型的可靠性；

(2)带端封及周向油槽供油的SFD能提供较大阻尼，且在端封的密封效果较好的情况下，SFD阻尼值对流量的变化不敏感；

(3)带端封及周向油槽供油的SFD将会使过转子的一阶临界的峰值转速提高；

(4)当转子—支承系统的阻尼比ζ能到8%附近，则SFD阻尼设计是有效的；

(5)当设计的SFD能提供较大阻尼时，能有效抑制过临界时振动响应，减振效果一般大于60%。