油槽设计对轴承润滑性能的影响研究

钱仲楷

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

轴承作为机械设备中关键的零部件，其良好的润滑性能能够保证机械设备稳定和可靠的运行，随着对于各类机械设备的结构要求的不断提高，对于轴承润滑性能的要求也日益增加。油槽结构对轴承润滑性能有着较大的影响，基于雷诺方程的传统研究方法有很多局限性，计算结果精度较低。随着计算机技术的不断发展，利用计算机辅助来求解控制方程，不仅可以获得更高精度的解，还可以大大降低计算的人工成本，节约计算时间。这种计算机辅助方法，即CFD（计算流体动力学）方法，使许多工程问题的润滑计算更接近于实际工况，得到了广泛的应用。

专家学者对于油槽参数进行了大量的研究。沈江[1]等对动静压轴承的润滑特性规律及其设计进行了较深入的研究，分析了主要油槽参数对轴承特性的影响，为轴承的设计开发提供了理论依据；王东强[2]等采用了四因素三水平的正交实验法，对轴承的油槽分布情况进行研究，分析了对轴承静态特性的影响，得出了各个轴承参数对于轴承静承载力的影响关系，为参数设计提供理论基础；吴健康[3]等通过求解雷诺方程，分析了不同参数下油槽结构对油膜稳定性的影响，发现合理的选择参数可以得到良好的油膜稳定性；徐晓秋[4]针对不同结构形式的油槽类型，分析不同结构类型轴承的性能，通过对比总结出不同结构轴承的适用工况，为轴承的设计选型提供了理论依据；禹洪亮[5]等考察了轴承润滑性在不同参数条件下的变化规律，找出了指定工况下最佳的轴承间隙，为轴承结构的设计优化提供了参考依据。

相对而言，目前对于轴承油槽参数的研究主要集中在小型轴承上，对于大型轴承的研究较少[6]，且采用CFD 方法分析大型轴承的油槽参数对轴承润滑性能的研究也较为稀少[7]。基于上述的研究，本文以某发动机轴承为研究对象，采用CATIA 软件建立了轴承内各结构的流体三维模型，利用PumpLinx 软件对流体三维结构模型进行网格划分和仿真分析，根据仿真结果，提取油膜压力分布、流速分布的数据，比较在不同油槽参数下、不同偏心率对这些特性参数的影响，发现合理的选择油槽参数可以提高油膜的稳定性。

1 模型建立

1.1 轴承内流体三维模型的建立

本文研究的是某发动机曲轴主轴承，其流体三维模型由进油口内流体、进油槽内流体、油膜3 部分组成，如图1 所示。

图1 流体模型三维图Fig.1 3D drawing of fluid model

在凹槽模型下方是油槽模型。本文使用的周向油槽结构，油槽模型有8 个圆形油槽，以轴向中心成对称分布，单侧油槽有4 个，在圆形油槽上方有一环形油层，厚度为3 mm，宽度与圆形油槽直径一致，如图2 所示。

图2 油槽结构图Fig.2 Oil tank structure diagram

1.2 网格划分

网格划分的好坏直接影响仿真计算的结果，如果网格划分得不够好，计算结果会出现无法收敛，或者计算结果不准确的现象，但如果网格精度太高，过多的网格数量在计算时会造成计算机运行过慢甚至死机，所以合理划分网格也是关键的一步。

PumpLinx 软件拥有自带的网格划分模块、general mesh 模块、templete mesh 模块。将该模型分成进油口、油槽内流体、油膜3 部分。模型局部网格图如图3 所示。

图3 模型局部网格Fig.3 Local mesh of model

对于前两个部分，选择general mesh 部分生成六面体网格，最大网格面积设置为1 mm，油膜部分采用templete mesh 模块，设置为一个偏心圆环网格，网格大小设置为200:5:20,最终完成对整个结构的网格划分设置。

1.3 控制方程

在仿真分析中，轴颈与轴瓦的间隙部分为油膜边界。润滑油在轴颈转动时，由于润滑油粘性被强制转动，在PumpLinx 的仿真计算中，其流体模型遵守质量守恒方程和能动量守恒方程。

（1）质量守恒方程

润滑油在轴承内狭窄的间隙内流动，在产生动压润滑时遵循了质量守恒方程，即连续性方程，为

式中：ρ——流体密度；t——时间；u——x方向上流体的流速；v——y方向上流体的流速；w——z方向上流体的流速。

由于仿真中设定流体为不可压缩，密度ρ为常数，质量守恒方程变为

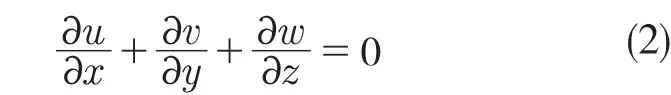
（2）动量守恒方程

本文中，润滑油为牛顿型流体，因此在仿真设置时粘度设定为定值，考虑不可压缩流体的动量守恒方程为

1.4 边界条件及模型假设

假设：（1）润滑油在轴承运转中不断被挤压，润滑油从进油口进入，从两端流出；（2）润滑油的粘性力远大于惯性力，因此可以忽略惯性力的影响。（3）本文仿真为一定偏心率和偏心距位置下轴承油膜压力分布，不考虑温度和黏度变化对油膜压力的影响，仿真条件中不求解能量方程。

2 仿真分析

2.1 不同油槽深度下的仿真结果分析

本文研究发动机轴承偏心率和油槽深度对最大油膜压力的影响，选定偏心率0.9，0.7，0.5，0.3 的轴承为研究对象，将其三维建模后放入PumpLinx 中进行仿真，结果如图4 所示。

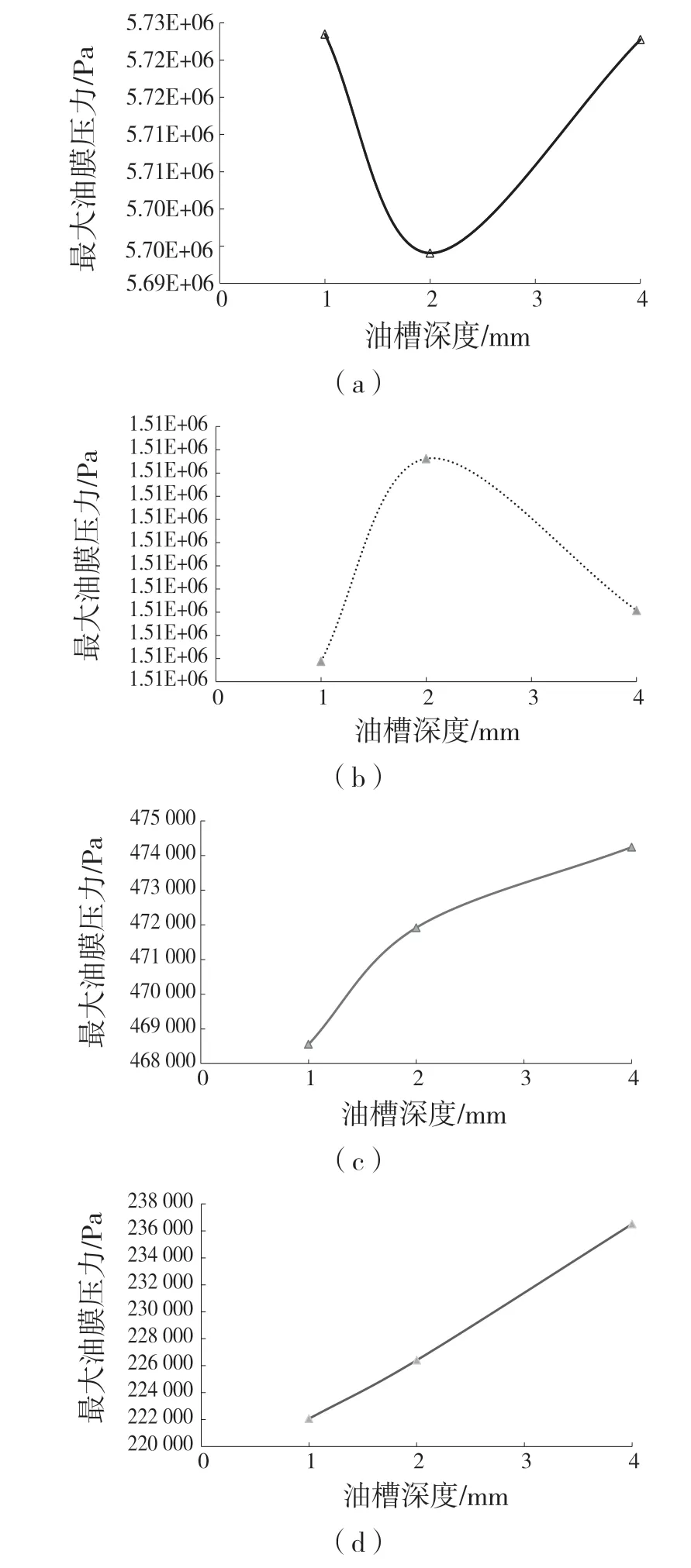
图4 不同油槽深度的最大油膜压力Fig.4 Maximum oil film pressure at different sump depths

图5 中显示，油膜最大静压力随着偏心率的增大而迅速增大。当偏心率为0.3 时，不同油槽深度的油膜最大静压力都约为0.4 MPa，其中油槽深度为1 mm 的油膜压力仅为40 763 Pa；当偏心率达到0.9 时，不同油槽深度的油膜最大静压接近6 MPa，而且增幅的百分比达到73.61%。

图5 不同偏心率油膜偏位角的变化Fig.5 Change of oil film deflection angle with different eccentricity

然而，随着油槽深度的增加，油膜最大静压并没有逐渐增大。偏心率为0.7，0.5，0.3 时，不同油槽深度的油膜最大静压相差不大，最高仅相差200 Pa；当偏心率为0.9 时，油槽深度为2 mm 的油膜最大静压力最小，与其他油槽深度的油膜最大静压相差接近0.5 MPa。这表明油槽深度影响油膜的最大静压力，但并不与静压力呈正相关。

这说明了不同偏心率下油膜偏位角的变化规律。通过仿真结果得出，不同油槽深度的油膜偏位角在相同偏心率下结果基本一致，说明油槽深度的变化对油膜偏位角的影响较小。偏位率对油膜偏心角有重要影响，油膜的偏位角对轴承的稳定性起着重要的作用，较低的油膜偏位角将提供更大的承载能力。随着偏心率的升高，油膜的偏位角略有增加，但当偏心率到达0.9 时，油膜的偏位角反而从171.4°下降到158.3°，这表明随着油膜偏心率的升高，油膜偏位角的变化趋势是先缓慢升高，然后出现一定的下降，但下降程度不高。

图6 显示了不同油槽深度轴承内油的流速情况。在92°～258°，不同油槽深度的流速分布基本相同；在0°～92°，轴承内油流速的大小随着油槽深度的降低而升高，并且变化趋势明显。

图6 不同油槽深度下流速的分布Fig.6 Distribution of flow velocity at different oil tank depths

在油槽深度为4 mm 时，轴承内油流速基本趋于0，但随着油槽深度的减少，当油槽深度为1 mm 时，轴承内最大流速达到了12.8 m/s；在300°～350°，油槽深度越小，轴承内油的流速就会越快。这一趋势表明，在轴承周向0°～92°和300°～350°的范围内，油槽深度的大小对轴承内油的流速的大小有较大的影响，同时随着偏心率的降低，该影响逐渐减小；当偏心率到达0.3 时，轴承内油的流速大小变化差值达到最小。

2.2 不同油槽宽度下仿真结果的分析

图7 显示了油膜最大静压力变化与上文的结果一致，随着偏心率的增大而增大，当偏心率为0.3 时，不同油槽宽度的油膜最大静压力都约为0.42 MPa，其中油槽宽度为16 mm 的油膜压力仅为40 763 Pa，当偏心率达到0.9 时，不同油槽宽度的油膜最大静压接近6 MPa，而且增幅的百分比达到72.35%。

图7 不同油槽宽度度的最大油膜压力Fig.7 Maximum oil film pressure with different width of oil groove

然而，随着油槽宽度的增加，油膜的最大静压并没有逐渐增大，随着油槽宽度的逐渐增加，油膜的最大静压力逐渐减小。

如图8 所示，在偏心率为0.7，0.5，0.3 时，虽然油膜的最大压力随着油槽宽度的增加逐渐下降，但差值不明显，最大仅为156 MPa,，但当偏心率为0.9 时，油槽宽度为6 mm 的油膜最大静压力最大，与油槽宽度为16 mm 的轴承相比，油膜最大静压力差值约有0.7 MPa，但与油槽宽度为12 mm 的轴承油膜最大静压力相差不大，这表明油槽宽度对油膜最大静压力的影响随着偏心率的升高逐渐变大，在油槽宽度为油膜宽度的8%～12%时，油膜的最大静压力差距不大，但随着油槽宽度的升高，油膜的最大静压力会出现陡降的趋势。

图8 不同偏心率油膜偏位角的变化Fig.8 The change of oil film deflection angle with different eccentricity

图9 显示了不同油槽宽度轴承内油的流速情况。在92°～258°，油槽宽度越小的轴承内油的流速越小，油槽宽度为8 mm 的轴承内油的流速基本为零，在0°～92°，轴承内油流速的大小随着油槽宽度的降低而升高，并且变化趋势明显。在油槽宽度为8 mm 时，轴承内油流速最大。随着油槽宽度的增加，当油槽深度为12 mm 时，轴承内最大流速达到了16.5 m/s，在300°～350°，油槽宽度越小，轴承内油的流速就会越快。这一趋势表明，在轴承周向0°～92°和300°～350°的范围内，油槽深度的大小对轴承内油的流速的大小有较大的影响，同时随着偏心率的降低，该影响逐渐减小，当偏心率到达0.3 时，轴承内油的流速大小变化差值达到最小。

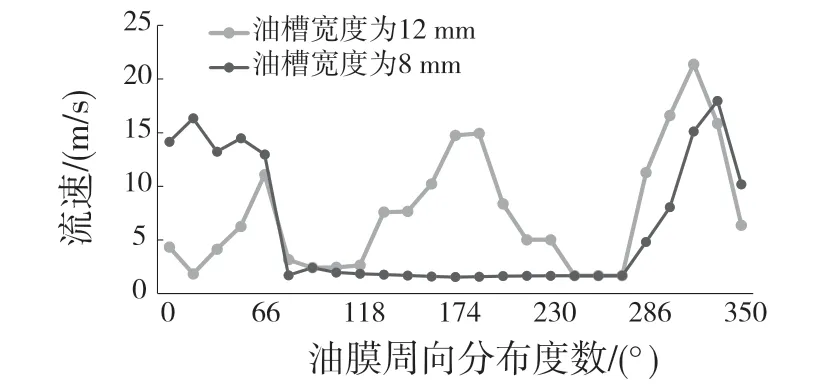
图9 不同油槽宽度度下流速的分布Fig.9 Velocity distribution under different width of oil tank

3 结论

当偏心率越大时，最大油膜压力也随之变大。在偏心率较小时，最大油膜压力的变化不是十分明显，在偏心率超过0.7 后，最大油膜压力有了显著的提升。

油槽深度增加，油膜的最大静压并没有逐渐增大。在偏心率为0.7，0.5，0.3 时，不同油槽深度的油膜最大静压相差不大，最高仅相差200 Pa；当偏心率为0.9 时，油槽深度为2 mm 的油膜最大静压力最小，与其他油槽深度的油膜最大静压相差接近0.5 MPa。这表明油槽深度影响油膜的最大静压力，但并不与静压力呈正相关。

油槽宽度对油膜最大静压力的影响随着偏心率的升高逐渐变大，在油槽宽度为油膜宽度的8%～12%时，油膜的最大静压力差距不大，但随着油槽宽度的升高，油膜的最大静压力会出现陡降的趋势。

油槽宽度与油槽深度的变化均会对轴承内油的流速产生较大的影响，不同的是随着油槽深度的增加，在轴承周向0～92°和300°～350°之间，轴承内油的流速会逐渐降低趋于0，在92°～300°之间，流速会出现显著的增大。而随着油槽宽度的不断增加，在轴承周向0～92°和300°～350°之间，轴承内油的流速会出现显著的上升趋势，在92°～300°之间，流速会出现陡降的情况，流速趋近于0。