基于CFD的超临界翼型气动特性数值模拟

，，

(1.上海理工大学能源与动力工程学院，上海市动力工程多相流动与传热重点实验室，上海 200093；2.中电投珠海横琴热电有限公司，广东 珠海 519031)

0 引言

近年来，在蒸汽轮机的末级与燃气轮机等动力装置中，跨音速叶型得到了广泛的应用，其具有改善叶轮机械内部气动特性的特点已经得到了普遍认可。超临界翼型是由美国国家航空航天局在1967年提出的，是一种为提高临界马赫数而采取的特殊翼型，能够使机翼在接近音速时阻力剧增的现象推迟发生，在航空航天领域得到广泛使用[1]，并发展出了超临界翼型族[2]。对于超临界翼型在跨音速叶轮机械的应用，尚未有研究。因此，对超临界翼型的气动特性进行研究具有重要意义，可为超临界翼型在跨音速叶轮的应用提供理论依据。

在跨声速条件下，超临界翼型表面容易产生激波，有效地减少跨声速流动中的激波损失和随之产生的边界层分离损失，避免或推迟激波的产生，是叶型研究的主要内容。许新等[3]利用数值求解的N-S方程，讨论了雷诺数对超临界翼型激波位置和激波强度的影响规律，结果表明：随着雷诺数的增加，超临界翼型上表面激波位置后移，激波强度增强。陆超等[4]通过对翼型进行多种方案的改型，得出了最终优化改型方案，使改型后翼型升阻比和临界马赫数均有显著提高。唐晓雷等[5]通过对某高压涡轮进行气动优化设计，对跨音速气冷涡轮的效率进行了研究，得出其效率提高的主要原因是优化后导叶中激波损失、二次流损失的减小以及动静叶匹配的改善。L.Sciacovelli等[6]研究了稠密气体效应对跨音速ORC(Organic Rankine Cycle)透平的影响，认为在相同流体和压力比条件下，超临界入口的跨音速透平等熵效率更高。

本文采用数值模拟方法，研究了超临界翼型SC(2)-0712在不同攻角和马赫数条件下，翼型升力系数、阻力系数及升阻比的变化规律，总结了翼型攻角变化对翼型气动力特性的影响。通过对三种超临界翼型相同条件的数值模拟，研究了攻角变化对翼型激波位置和激波强度的影响。

1 数值研究方法

1.1 湍流模型

本文采用SSTk-ω湍流模型，其全称是剪切应力输送(shear-stress transport)k-ω模型，是一种得到广泛应用的两方程混合模型，它在近壁面区域采用Wilcox的k-ω模型，在边界层边缘和自由剪切层采用k-ε模型计算，其间通过一个混合函数来过渡，属于积分到壁面的不可压缩/可压缩湍流的两方程涡粘性模式[7]。

SSTk-ω湍流模型改进在于：(1)SSTk-ω模型和k-ω模型的变形增长与混合功能和双模型加在一起，混合功能是为近壁区域设计的，这个区域对标准的k-ω模型有效，还有自由表面对k-ω模型的变形有效；(2)SSTk-ω模型合并了来源于ω方程中的交叉扩散；(3)湍流粘度考虑到了湍流剪应力的传播；(4)模型常量不同。这些改变使得SSTk-ω模型比k-ω模型在广泛的流动领域中有更高的精度和可信度[8]。王科雷以RAE2822超临界翼型为研究对象，结合相关实验结果验证了该湍流模型的可靠性及准确性[9]。

1.2 网格划分

对数值模拟流场进行网格划分是数值模拟的基础，网格划分质量的好坏直接影响数值计算的结果。为了满足对计算区域几何形状的要求，计算中采用了翼型流场的C型结构化网格，并对翼型表面网格进行加密处理，无量纲翼型弦长取1，计算域的外边界各方向均取20倍翼型弦长。以翼型SC(2)-0712为例进行网格无关性验证，所得网格基本满足要求，网格数量为7万左右。计算区域网格示意图及翼面附近网格示意图分别如图1、图2所示，翼型表面网格高度不大于0.003 mm。

图1 计算区域网格示意图

图2 翼面附近网格示意图

1.3 边界条件

边界条件确定为：对于计算域外边界，用压力远场边界条件；翼型物面边界给定无滑移绝热条件。出口为压力出口边界条件，压力数值为大气压力。

2 数值计算及结果分析

2.1 气动力分析

本小节采用第1节建立的数值方法对超临界翼型SC(2)-0712不同马赫数的扰流特性进行模拟。选取马赫数分别为：0.75、0.78、0.82。图3、图4、图5分别为三种马赫数条件下升力系数(CL)、阻力系数(CD)及升阻比(K)曲线图。

图3 升力系数与攻角曲线关系图

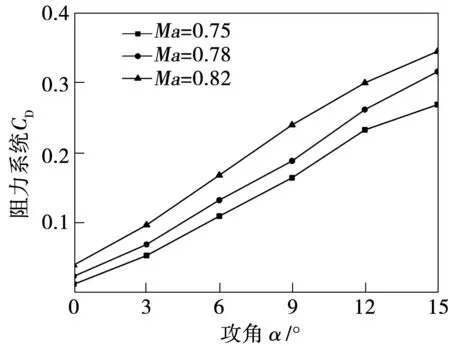
图4 阻力系数与攻角曲线关系图

图5 升阻比与攻角曲线关系图

由图3、图4、图5分析可以得出，随着攻角的增大，三种马赫数下升阻曲线随攻角的变化趋势大致相同：升力系数在9°～12°达到峰值后开始减小，阻力系数在研究范围内不断增加；升阻比在小于6°时变化明显，随着攻角不断增大，趋于平坦。

由图3可知，当攻角小于3°时，马赫数越大，其对应的升力系数越小；当攻角为3°时，三种马赫数下对应的升力系数近似相同；随着攻角的继续增大，此时，马赫数越大，翼型升力系数也越大。分析图4可知，三种马赫数条件下，阻力系数均与攻角呈近似线性变化，即攻角越大，阻力系数也越大；而当攻角相同时，阻力系数随着马赫数的增大而增大，而斜率与升力系数相比，变化并不明显，可以得出结论：翼型在小攻角条件下，马赫数的变化对翼型阻力系数的影响不大。图5中，攻角小于9°时，马赫数越大，升阻比越小；当其增加至大于9°后，升阻比几乎相同。

2.2 激波特性分析

本小节对三种超临界翼型DFVLR-R4、SC(2)-0712、SC(2)-0712进行数值模拟，分析了激波位置和激波强度随攻角的变化规律。

本文采用的激波位置定义方法如图6所示。该方法中，将经过激波后的压强跃升直线与垂直前缘马赫数MaLN=1时压力系数直线交点的横坐标，定义为激波位置xCSH[10]。激波强度没有统一的定义，本文将翼型上表面经过激波后压力的跃升作为激波强度标准。图7、图8分别是三种翼型在不同攻角条件下的激波位置和激波强度曲线图。

图6 超临界翼型激波位置定义

图7 翼型激波位置曲线图

图8 翼型激波强度曲线图

图7给出了马赫数为0.75时，激波位置随攻角变化的计算结果。由图分析可知，三种翼型激波位置变化规律基本一致，激波位置随着攻角的增大不断前移。攻角达到15°时，激波接近前缘。图8为相同马赫数时翼型激波强度随攻角变化的计算结果。可以看出，激波强度随攻角增大呈上升趋势。翼型SC(2)-0712相对另外两种翼型，变化更为剧烈，翼型SC(2)-0714相对较为平缓。

3 结论

(1)通过对超临界翼型SC(2)-0712不同条件下的数值模拟，得出：翼型升力系数随着攻角的增大先上升后下降，峰值在9°～12°攻角范围；阻力系数随着攻角增大而增大；升阻比随着攻角增大而减小，并在6°攻角之后趋于平坦。

(2)通过对三种超临界翼型的数值模拟，得出：攻角的变化对激波位置和强度有显著影响，攻角越大，激波越靠近前缘，激波强度也越大。