深挖教材感悟本质——《三角形的面积》教学

张永万

【教学内容】

人教版五年级上册第91～92页。

【教学过程】

一、知识铺垫，复习引入

师：上节课我们学习了平行四边形的面积，还记得是怎样推导的吗？

生：把平行四边形沿高剪开拼成长方形，长方形的长等于平行四边形的底，宽等于平行四边形的高，根据面积的大小没有发生变化，长方形的面积等于“长×宽”，得到平行四边形的面积等于“底×高”。

师：也就是把新知识转化成已学过的知识，利用新旧知识的联系我们把问题解决了。这里面有一种重要的数学思想是什么呢？

生：转化的思想。

师：对，转化的思想。今天我们来研究另外一种图形的面积——三角形。

二、合作探究，学习新知

1.动手操作，初步感知。

师：请每个小组从1号学具袋中拿出一个三角形和剪刀,利用转化的方法把三角形转化为学习过的图形。

（小组合作，教师巡视指导，发现问题或有价值的资源）

小组展示交流：（说说本组是怎样剪拼的？）

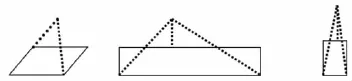
（1组）

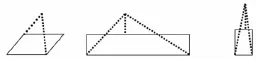
（2组）

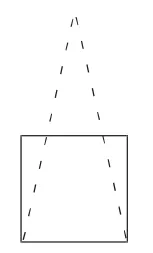
（3组）

师：同学们真会思考，把三角形分别转化成了平行四边形、长方形和正方形，很了不起，老师为你们自豪。同学们是否发现这三种情况在剪拼前都有一个对折的过程，其实是把高进行了对折，这种方法还需要剪刀，剪拼显得有点麻烦，是否有更简单一点的方法呢？

2.再次探究，深入理解。

师：老师在课件上出示许多三角形（直角三角形、钝角三角形、锐角三角形，不一样的一般三角形各两个），请从中选出若干个三角形拼成学过的图形。下面从2号学具袋中拿出学具（课件中的图形，各种三角形区别比较大），小组合作进行探究。

（小组合作，教师巡视指导）

（学具中只有选出完全相同的两个三角形才能拼成平行四边形、长方形或正方形。学生必须经历多次的观察合作探究实践，才能发现只有完全相同的两个三角形才符合要求）

师：交流怎样找到并拼成的？小组展示：

（1组）

（2组）

（3组）

（4组）

师：同学们的观察能力可真强，很快就找到了两个完全相同的三角形可以拼成平行四边形、长方形或正方形。我们知道长方形和正方形都是特殊的平行四边形，所以我们可以说都拼成了什么图形？

生：平行四边形。

3.讨论探究，直指本质。

师：请同学们看剪拼法中三角形与平行四边形面积的大小有什么关系？

生：图形发生变化，面积的大小不变。

师：面积的大小不变，讨论讨论平行四边形的底和高与三角形的底和高有什么关系？

小组讨论后汇报：

组1：第一幅图的平行四边形的底等于三角形的底，平行四边形的高等于三角形高的一半。

组2：第二幅图的长方形的长等于三角形的底，长方形的宽等于三角形高的一半。

组3：第三幅图的正方形的边长等于三角形的底，正方形的边长还等于三角形高的一半。

师：同学们的分析推理既正确又到位，把长方形和正方形都看成特殊的平行四边形，这三组的同学汇报可以看成哪一组的汇报？

生：第一组同学的汇报。

师：所以三角形的面积等于平行四边形的面积，可以得到怎样的三角形面积公式呢？

生：因为平行四边形的底等于三角形的底，平行四边形的高等于三角形的高的一半，平行四边形的面积是“底×高”，所以三角形的面积就等于“底×高÷2”。

教师板书：三角形的面积=底×高÷2

师：请看用两个完全一样的三角形拼成的平行四边形的四幅图，总结一下底与高之间的关系以及面积之间的关系。注意不要再分平行四边形、长方形和正方形，统一使用平行四边形来回答。

小组讨论后汇报：

组1：因为三角形的面积等于平行四边形面积的一半，三角形的高等于平行四边形的高，三角形的底等于平行四边形的底。根据平行四边形的面积公式“底×高”，可以得到三角形的面积公式为“底×高÷2”。

组2：我们组补充一点，只要是两个完全一样的三角形，都可以拼成与其中一个三角形等底等高的平行四边形。

师：同学们的总结归纳能力非常强。两种方法都推出了三角形的面积公式，里面的除以2表示的意思一样吗？

生：第一种表示平行四边形的高是三角形高的一半，第二种表示三角形的面积是平行四边形面积的一半。

师：那该如何理解和使用公式呢？

生：我们可以把“底×高”想成是与三角形等底等高的平行四边形的面积，除以2就得到三角形的面积。

师：回答得太漂亮了！想一想，怎样用字母表示三角形的面积公式？

生：在平行四边形的面积公式后添上“除以2”，就是“s=ah÷2”。

师：请同桌相互说一说，三角形的面积公式中为什么要除以2？

4.深化理解，底高对应。

师：你能帮老师找到求三角形面积的数据吗？

图1

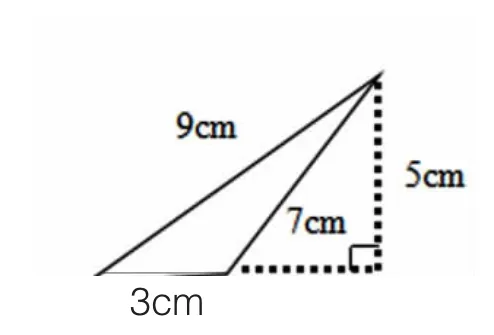
图2

生1：图1的底是12cm,高是10cm，所以三角形的面积应该是12×10÷2，其他的数据没有用处。

生2：图2的底是9cm,高是5cm,所以三角形的面积应该是 9×5÷2。

生3：他回答的不对，图2的底是3cm,高是5cm,所以三角形的面积应该是3×5÷2。师：大家赞成哪种意见呢？生：3×5÷2。

师：从这两道题中我们可以看出，找底与高要注意什么呢？

生：底和高要相互对应。

师：是的，我们在求三角形的面积时，一定要找准底边上的高，才可以正确地求出三角形的面积。在生活中我们能遇到许多求三角形面积的问题，请看练习。

三、练习巩固，内化新知

师：同桌每人一道题，请先说出三角形的底和高，再求值。

教师课件出示：（先出示第1题，再出示第2题）

1.红领巾的底是100cm，高是33cm，它的面积是多少平方厘米？

2.一种三角尺的形状如下图，它的面积是多少？

（学生交流汇报）

四、梳理新知，分享收获

师：同学们，通过这节课的探究交流，你一定收获了很多，谁能分享一下你的收获？

（学生分享收获）