从深刻性理解到结构化学习
——兼谈《20以内的进位加法(第一课时)》教学
许卫兵(特级教师)
如果从内容形式上划分,“20以内的进位加法”应当属于计算教学的范畴。但是,由于这是学生首次学习进位加法,首次正式学习并应用“凑十法”这一贯穿在整个加法运算中的重要算法,因此,本课教学又带有浓浓的概念教学的意味。深刻地理解和把握这一内容的学习重点,正确看待“凑十法”的学习价值与意义,寻求科学有序的学习方式和路径,是这节课需要考虑的几个重要方面。
对教学内容的深刻理解,并不能局限在教材内容。马立平博士在《小学数学的掌握和教学》一书中提及,深刻理解数学包括三个“度”:宽度、深度和完整度。所谓宽度,就是能多角度地“欣赏”一个概念的不同侧面和解决问题的不同路径,以及它们的优势与不足。所谓深度,就是“显示了积极的数学态度”,并特别清楚“简单而又强大的基本数学概念和原理(数学思想)”。所谓完整度,就是能够融会贯通——并不局限在某个年级的数学知识,而是对整个小学数学课程有全面把握。这种深刻理解,“不仅仅是对小学数学有很好的概念性理解,而且还是对小学数学中内在的概念结构和基本的数学态度的掌握,还有能为概念结构提供的基础并把那些基本的态度传授给学生的能力”。
如何从知识系统性的角度理解“20以内的进位加法”的教学呢?这是因为,是10以内加减法(即“不进位加”“不退位减”)的延续和升华,又是后续两位数(或多位数)加减法的基础。实际上,看似“高级形式”的多位数加减最终都是分解为一步一步的20以内的加减法来完成。因此,这一内容,在整个加减法的知识系统中“分量”非同一般。从马立平博士提供的加减法“知识包”(如下图)可以看出,“20以内加减法”与“进位和退位”(用深色加以标注),就是表明它们在整个知识系统中的关键作用,不仅承上启下,而且“左通右达”。
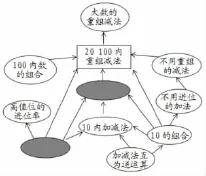
了解到这一重要性后,就需要进一步思考如此重要是通过什么来承载的,即到底是什么东西让“20以内的进位加法”变得如此重要?很显然,那就是“凑十法”在其中发挥的重要应用。因此,理解“凑十法”、学好“凑十法”、灵活应用“凑十法”就成了本课教学的重点。
纵观刘玉晗、钱丽两位教师的教学设计,都聚焦在“凑十法”上大做“文章”,颇有异曲同工之效:首先是借助具体算式或图示等直观手段激活“10”的感觉,唤醒“10加几等于十几”的运算经验;然后是尝试解决新问题(9加几),从算法多样化的背景中,将“凑十”的方法思路提取出来,聚焦并放大其在运算中的优越性;接着通过拓展、迁移、对比、应用,进行巩固练习,强化利用“凑十法”进行进位加法运算的熟练水平。应该说,这两节课在宽度、深度和完整度上都有充分的体现,并且教师努力将自己的理解转化成学生积极的学习行动与能力培养。客观地讲,这样的设计思路和教学组织在传统教学中是比较常见的,也在一定程度上印证了马立平博士在《小学数学的掌握和教学》中所述的观点——“中国教师往往对一个概念第一次被引入的场合最为重视。他们为后续的学习建立坚实的基础。对他们来说,第一次和最初的学习越牢固,它能为后续的形式更为复杂的概念学习提供更多的帮助。”
当然,同样是重视“凑十法”,两位教师的教学设计也体现出一定的差异。刘玉晗老师遵照教材的编排体例,第一课时只学习“9加几”。因为学习内容相对较少,因此课堂教学比较细腻,各部分展开比较充分,学习要求稳步提升,巩固训练比较扎实。钱丽老师不拘泥于教材的限制,将两个课时的内容整合在一节课学习(实际上还涉及到第三课时编排的部分内容),以“凑十法”的学习为主线,串联起9加几、8加几、7加几的学习,学习容量相对较大,思维要求相对较高,不过,因为课堂“主线”清晰,迁移过渡比较自然,加上学生已有的知识基础的支持,学起来也不见得有太大困难。更为重要的是,因为其跨度大,重视了知识间的整体性和结构关联,学生经历了较为完整的认知建构过程,结构化思维得到了很好的发展。
钱丽老师的教学设计触发了我们对结构化学习的思考。所谓结构化学习,是指建立在数学知识系统和学生已有认知基础之上的,以整体关联为抓手,以动态建构为核心,以发展思维为导向,以基础学力与数学素养为目标追求的学习过程、学习方式和方法。数学常常就被说成“结构的科学”,一方面是因为郑毓信教授在《新数学教育哲学》一书中提到“数学对象是明确定义的产物,数学结论又是按照相应的定义与给定的推理规则进行推理的结果,因此,数学对象的性质就完全反映于它们的相互关系。这也就是指,数学对象的建构事实上是一种整体性的建构活动。或者说,数学的对象并非各个孤立的模式,而是整体性的建构”;另一方面也是因为学习总是一个连续的过程,前面的知识支持新的知识,新知识又加强和深化了原先的认识,用美国认知心理学家布鲁纳的话来讲,即“学习就是认知结构的组织和重新组织,学习结构就是学习事物是如何联系的”。
正因为数学知识系统具有很强的整体性、逻辑性、结构性,因此,数学学习要充分顺应这种特征,抓住知识间的内在联系,让学生在建构性学习中更好地把握结构、理解结构、生成结构,发展结构化思维,提升数学素养,催生数学学习的智慧。受钱丽老师的教学设计的启示,我们可以发现,很多数学内容的学习都是可以适度整合的,比如:借助于真实的钟面,将“时”“分”“秒”三个时间单位安排在一节课学习;在学习“分米”和“毫米”时,将之嵌入到“米”和“厘米”的序列中。经过整合,能少用课时,增强学习效果。当然,我们不能为了整合而整合,还需要充分考虑学习基础、学习难度、学习容量。同时,也要看到,“结构”的存在方式是多种多样的,从范围来看,有大结构(比如,小学里学习的认识方向、确定位置,实际上都是初中学习的直角坐标系模型;长方形、正方形、三角形、平行四边形的面积都可以用梯形面积公式来计算,内在具有“统一性”等)、小结构(比如,钱丽老师教学设计中,开始五道含有“10”的加法算式的比较,中途将“9+4”的多样化算法进行比较,最后环节将“进位加”和“不进位加”进行比较等,都具有明显的结构特色)。从内容上来看,有知识层面的(比如,用“凑十法”计算进位加),也有方法层面(比如,钱丽老师的教学设计中出现的“看、提、摆或圈、写、说”的问题解决流程;用“先分后合”解决多位数乘法运算等);有思维层面的(比如,正想想,反想想),也有思想层面的(比如,转化的思想、建模的思想、方程的思想等)。从时序上看,有学习前结构(原有的认知结构)和学习后结构(经过学习之后形成的新的认知结构)。从对象上看,有个体结构(学生个人具有的结构方式)和群体结构(学生集体拥有的结构模式)。多样化的结构形式,必然会带来多样性的结构化学习,当然,其根本的目标还是促进思维的发展,尤其是结构化思维的发展。
总的说来,对教学内容的深刻性理解是有效进行教学活动和学习活动的前提,而结构化学习则是具体的过程、路径和方式,它遵从了数学学科“整体性建构”的本质特征,顺应了数学学习“四两拨千斤”的内在需求,彰显了“素养为上”的教育教学价值,值得我们好好地思考和实践。

