基于多特征i-vector的短语音说话人识别算法

孙 念,张 毅,林海波,黄 超

(1.重庆邮电大学 先进制造工程学院,重庆 400065; 2.重庆邮电大学 自动化学院,重庆 400065)(*通信作者电子邮箱599217746@qq.com)

0 引言

说话人识别(Speaker Recognition, SR)就是根据说话人的声音特征来判断其身份的一种生物特征识别技术,也被称为声纹识别(Voiceprint Recognition,VR)[1]。时至今日,说话人识别发展已有50余年,研究者发现不同说话人的声学特征有一定的差异[2]。

文献[3]在语音环境干净的情况下,基于i-vector的说话人模型具有高识别率。然而,如果训练与测试语音不匹配,会使说话人识别系统性能显著下降。背景噪声、信道失真以及说话人之间的个性特征差异等是造成这种失配的主要原因。此外,声学建模需要有足够的数据支撑,例如深度神经网络(Deep Neural Network, DNN)[4-5]。所以,说话人识别系统想要获得高性能,训练和测试语音数据充足是一个重要的前提。但在实际应用中,从用户那里收集足够的数据是不可能的,且违背了语音人机交互的友好性,这给现有的方法带来了很大的挑战。根据美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)的定义[6],如果训练或测试语音的长度小于10 s,说话人识别就被称为短语音说话人识别(Short Utterance Speaker Recognition, SUSR)。尽管传统的单特征方法在具有足够测试语音数据时已经获得了出色的性能,但是在本文的短语音说话人识别实验中，它们的性能欠佳。目前,语音领域的研究者已经开始重视这方面的研究,并开展了一些很有意义的科研工作,但是总体来说短语音研究依然处于起步阶段[7-9]。

在说话人识别领域,声学特征的合理选择十分重要。如果选取的声学特征不能掌握说话人的个性特性,那么即使是最先进的机器学习算法[10-11],也不可能使系统达到一个良好的识别效果。目前,已有研究表明测试语音时长充足时,单一声学特征的信息量和区分性足够完成说话人识别任务。然而,在短语音条件下,只使用单一的梅尔频率倒谱系数(Mel-Frequency Cepstrum Coefficient, MFCC)特征建模,不能充分表达说话人个性信息,这使得系统难以取得良好的识别效果。考虑到不同的特征可以表征说话人不同的个性信息,多特征融合代表了更多的说话人信息,这在短语音条件下具有一定的优势。然而,最简单的多特征融合方法就是将每一帧语音信号提取的多种声学特征直接连接成一个大的高维向量。但是在实际中这种做法是不可取的,因为不同的特征之间并非正交,直接相连会相互影响,而且不同特征直接相连后会变成一个高维空间向量,提高维度意味增加了系统的复杂度;此外,其中很多维信息之间存在一定的重复,会产生冗余信息。因此可以通过降维算法把高维空间向量映射到低维空间中,选取其中最具有区分性的部分。

基于此,本文首先选择不同声学特征组合,解决单一特征不能很好表达说话人个性信息的问题；其次,希望采用主成分分析(Principal Component Analysis, PCA)算法和线性判别分析(Linear Discriminant Analysis, LDA)算法克服多种声学特征简单组合的局限性[12],进一步提高说话人识别系统性能。

1 i-vector说话人模型

i-vector系统用一组低维总体变化因子矢量代表一段语音,将每个说话人的一段语音的高维高斯均值超矢量s分解为:

s=m+Tw

(1)

其中:m为一个与特定说话人和信道无关的超矢量;T为全局差异空间；将高维高斯混合模型均值超矢量在该子空间上进行投影,得到低维的总体变化因子矢量w,w为包含整段语音中说话人和信道信息的一个全局差异因子,即i-vector。

在i-vector模型中,假定来自第i段语音的第t语音帧xt(i)分布如下:

(2)

其中:K为通用背景模型(Universal Background Mode, UBM)高斯分量的混合数;Tk为矩阵低秩子空间;ω(i)是特定语音段i符合标准正态分布的隐藏因子;μk和Σk分别是第k个高斯分量的均值和协方差;γkt(i)为xt(i)对第k个高斯分量的后验概率。γkt(i)的计算公式为:

γkt(i)=p(k|xt(i))

(3)

语音段的i-vector为隐藏因子ω(i)的极大后验点估计,也是隐藏因子的后验均值。对给定的一段语音,各阶统计量计算如下:

(4)

(5)

(6)

其中:Nk、Fk和Sk依次表示为零阶、一阶和二阶统计量。这些统计量是用来训练子空间矩阵T并提取i-vector所需要的全部数据。

2 PCA和LDA

2.1 PCA

在大多数情况下,为了减少计算量,本文假设高斯混合模型(Gaussian Mixture Model, GMM)的每个协方差矩阵都是对角矩阵。这就意味着具有不相关和正交的特征向量可以通过使用GMM实现最优的性能,而具有相关和非正交的特征向量的估计可能只是近似实际分布,造成各阶统计量计算不准确,从而影响说话人识别性能。值得注意的是,不同特征的基向量也可能是相关和非正交的,如果直接把这些特征连接起来,那么估计的充分统计量也会不够准确,导致最后的i-vector模型决策的准确度也不高。为了解决这个问题,在本文算法中使用PCA来保持总特征空间的基向量不相关和正交,即去除特征向量之间的相关性。

假设输入数据矩阵x,具有行零经验样本均值,其中：n列中的每一个xi表示实验的不同线性组合；x的平均值为0；ω假定为单位方向向量。 在ω方向上的协方差矩阵如下:

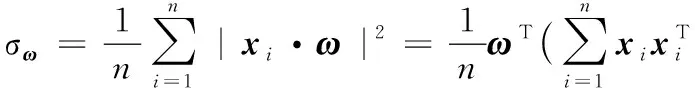
(7)

max{ωTΣω}；ωTω=1

(8)

f(ω)=ωTω+λ(1-ωTω)

(9)

(10)

要使方程(10)成立的条件是让投影矩阵的协方差最大化。显然,解方程(10)相当于计算特征值λ和特征向量ω,σω计算如下:

σω=λωTω=λ

(11)

这意味着λ越大,σω越大。 值得注意的是,Σ是实对称矩阵且其特征向量之间是正交的,因此前M个最大特征值对应的特征向量所生成的投影矩阵ωPCA可以将D维空间映射到具有最大协方差的M(M≤D)维空间:

ωPCA=[ω1ω2…ωM]

(12)

2.2 LDA

PCA算法的好处是能够简单直接地对数据进行降维和正交化,但是由于PCA算法是一种无监督的学习方式,只是将所有数据整体映射到最能体现这组数据整体区分性的坐标上,并未利用不同类别的数据关系来进行数据分析。为了弥补这种不足,使用LDA这种监督学习方法,可以利用数据上的分类标签,在低维空间上寻找不同类别数据间的最大区分性,对分类问题很有帮助。

对于处于n维空间Rn上的带标签数据集X,总数据量的数据点数为N,总数据类数为C,其中第i(i∈[1,C])类的数据集Xi包含Ni个数据点,所以N1+N2+…+NC=N,根据上面的定义可以计算第i类数据集的样本均值μi和总体样本均值μ分别为:

(13)

(14)

LDA可以使数据经过投影以后,达到最小的类内方差和最大的类间方差,所以需要计算各类的类内离散度SW和不同类之间的类间离散度SB为:

(15)

(16)

其中:ω为高维空间Rn向低维空间映射的投影矩阵。根据LDA的优化准则有:

(17)

对于方程(17)的求解,相当于对方程SBωi=λiSWωi求其最大的L(L≤C-1)个特征值和它对应的特征向量。

3 本文方法

在本文算法中，通过组合起来的语音特征向量进行了一个整体的变换形成一个新的特征向量。训练和测试语音被分成许多帧,其中部分帧之间有重叠,所以从每帧中提取所有类型的特征向量。那么其中一段语音信号中提取的所有不同特征向量,可以由如下的M维长特征向量(1≤M≤H)表示：

(18)

其中:H表示划分的语音帧数；C表示提取的特征类型数。用倒谱均值减(Cepstrum Mean Subtraction, CMS)使各列的样本均值为零,这样可以有效降低信道和噪声的影响。

在特征提取之后,把所有特征通过PCA方法计算投影矩阵。值得注意的是，特征矩阵F是由行向量组成的,因此特征矩阵F的协方差矩阵计算如下:

σF=FTF

(19)

显然σF是对角化的,因为它是一个对称矩阵。那么特征矩阵的协方差σF可以分解如下:

(20)

其中:ωi是特征值λi对应的归一化特征向量。假设λ1≥λ2≥…≥λt,那么投影矩阵ωPCA可以有前p个最大特征值对应的特征向量生成,如下:

ωPCA=[ω1ω2…ωp]

(21)

ωPCA用于将所有特征向量映射到不相关和正交的特征空间,包括UBM、训练和测试的特征向量，则经过PCA方法变换后的新特征可以表示为:

(22)

在去相关的基础上,进一步采用LDA方法使特征具有更好的区分性。相当于求解方程SBωi=λiSWωi,取前L个最大非零特征值对应的L个特征向量(L≤C-1)则为最优解,可以表示为:

ωLDA=[ω1ω2…ωL]

(23)

(24)

其中:特征矩阵FH×M的维数M根据计算LDA变换时选取的特征根和特征向量的不同,其维数也不同,需要根据特征根占全局的比重来选取合适的最具区分性的特征部分(特征根比重大于99%)。

在将所有特征变换到不相关且正交的特征空间之后,可以从训练语音中提取的部分语音训练UBM模型。然后根据UBM模型和训练数据,运用i-vector方法生成每一个说话人模型。其中,从语音数据里提取的训练和测试语音特征需要经过整体变换矩阵映射到同一个特征空间。最后将变换后的测试特征向量与目标说话人特征向量进行得分判决。本文算法的整体框架如图1所示。

图1 本文算法总体框图Fig.1 Overall diagram of proposed algorithm

4 实验结果与分析

4.1 数据库与实验设置

实验是在TIMIT数据库150位女性数据和150位男性数据上进行的,采样率为16 kHz,采样位数为16 bit,每人10段语音,句子长度1～10 s不等,利用HTK工具对语音信号进行预处理和特征提取,选用的特征有13维MFCC(不包括C0和C1)[13],20维感知对数面积比(Perceptual Log Area Ratio, PLAR)[14]和12维线性预测倒谱系数(Linear Prediction Cepstrum Coefficient, LPCC)。选取train文件里的dr1～dr8中的数据训练UBM,随机挑选30段作为训练整体变换矩阵使用;选取test中的dr1～dr8中的50名男性和50名女性数据作为测试数据。测试语音中每个人的6段语音用来训练说话人模型,其余4段可随机截取为7种不同长度(0.5 s,1 s,2 s,4 s,6 s,8 s,10 s)的语音用来测试。

对于特征提取的参数在处理过程中尽量保持相同,首先语音分帧参数相同,帧长为20 ms,帧移为10 ms。此外,预加重系数选取为0.97,使用汉明窗作为窗函数,Mel滤波器个数定为30。

本文使用两个基线系统:经典的GMM-UBM说话人识别系统以及标准的i-vector说话人识别系统。其中,GMM-UBM模型包含1 024个高斯混合数,每个高斯的协方差矩阵为对角阵。训练全局差异空间矩阵T的语料与训练UBM的语料一致,全局差异空间矩阵采用随机初始化,迭代6次,最终得到全局差异空间矩阵。基线系统的特征被设定为多特征系统中使用特征的适当子集,本文基线系统仅使用13维(不包括C0和C1)MFCC作为特征进行比较,从13维MFCC中提取400维的i-vector。

4.2 实验结果和分析

作为说话人识别系统最常用的评价指标,NIST的等错误率(Equal Error Rate, EER)和检测代价函数(Detection Cost Function, DCF)被用来比较基线系统和本文方法,DCF的有效先验部分在NIST SRE’10[6]中定义为0.001。

首先,通过Matlab的降维工具包drtoolbox在TIMIT数据库上对直接相连的45维特征向量进行降维,找出最具区分性的特征部分,不同降维程度对两种基线系统的性能影响如图2。可以发现针对两种基线系统,当特征维数在30维左右时,说话人识别系统的性能达到最优;而当特征维数超过30以后,特征向量所包括的说话人信息的增加速度远低于区分性信息的增加的速度,所以导致系统性能呈下降趋势。因此,多特征变换系统的特征维数为前30维。

图2 不同维度对两种基线系统性能的影响Fig.2 Effects of different dimensions on the performance of two baseline systems

接着,对不同特征在两种基线系统下的性能进行比较,其中测试语音长度保持在2 s,不同特征在短语音条件下的系统性能(EER)对比如表1。可以发现短语音条件下的不同特征将直接影响系统性能,其中:LPCC特征的结果最差,PLAR特征的性能相对比较好,MFCC特征性能居中；同时也说明不同特征之间存在一定的差异。但是单纯地将三种特征向量直接相连后的实验结果却不如任意一种单一特征系统,这也验证了本文对于多种特征直接组合是不可取的观点,因为特征之间虽然存在互补性,但是不同的特征之间的向量并不是完全正交的,它们在空间中会相互影响。针对以上问题,可以发现本文提出的多特征变换算法的系统性能优于单特征系统。具体结论如下:在GMM-UBM说话人识别系统中,本文提出的多特征变换算法相对三种单特征系统的EER分别下降了35.76%、34.14%和44.37%;而对于i-vector说话人识别系统,分别下降了72.16%、69.47%和73.62%。对比两种系统的多特征组合变换算法的实验结果,i-vector说话人识别系统相对于GMM-UBM说话人识别系统有66.80%的降低,这验证了多特征i-vector说话人识别系统在短语音条件下的有效性。

表1 短语音条件下不同特征性能比较Tab.1 Performance comparison of different features under short speech condition

最后,针对不同的短语音长度,分析不同语音长度对系统的影响,两种基线系统和提出系统的EER和DCF的性能比较如表2所示。 从表2可看出：与两种基线系统相比,本文算法在实验中表现出最好的性能。与具有单一特征的i-vector系统相比,本文算法的EER和DCF减小50%；另外,当测试语音长度大于4 s时,本文算法能保持相对较低的EER,而单一特征系统的性能却迅速下降。这表明了从语音中提取更多信息来弥补数据缺失,能使短语音说话人识别系统性能更好。

表2 不同语音长度下说话人识别性能比较Tab.2 Comparison of speaker recognition performance under different speech lengths

5 结语

本文提出了一种基于多特征i-vector的短语音说话人识别系统算法。首先从语音段中提取了MFCC、PLAR、LPCC三种具有说话人不同特性的特征进行了组合,解决单一特征说话人信息量不足的问题；然后采用主成分分析法(PCA)进行多种不同特征之间的去相关,使得特征之间相互正交化；最后为了提取说话人类内和类间数据更具区分性的部分,采用线性鉴别分析法(LDA)对特征向量进行处理,得到新的多特征向量作为i-vector说话人模型的输入进行说话人识别。用TIMIT语料库的在Matlab 2015b上进行实验验证了本文算法的可行性和有效性。