基于不确定服务质量感知的云服务组合方法

王思臣,涂 辉,张以文

(1.计算智能与信号处理教育部重点实验室(安徽大学), 合肥 230031;2.瓦斯治理国家工程研究中心(淮南矿业集团), 安徽 淮南 232001)(*通信作者电子邮箱zhangyiwen@ahu.edu.cn)

0 引言

随着云计算的发展,越来越多的资源以服务的形式发布和使用,如何选择高性能的服务来构建增值的应用已成为研究热点。服务通常由功能属性和非功能属性构成,非功能属性也称为服务质量(Quality of Service, QoS),描述了服务在完成其功能的过程中表现出的执行特性,由响应时间、吞吐量、延迟、成功率、花费、信誉度等一系列属性构成。然而,在许多情况下,单个服务是无法满足用户复杂需求的,需要根据用户需求进行服务组合。由于功能属性相似而非功能属性不同的服务数量迅速增加,服务选择变得越来越复杂,使得服务组合问题逐渐演变为NP(Non-derministic Polynomial)完全问题。为了高效地找到最优服务组合,许多方法被相继提出。常用的方法有整数线性规划(Integral Linear Programming, ILP)、混合线性规划(Mixed Linear Programming, MLP)和人工智能(Artificial Intelligence, AI)算法[1-7]。然而,这些方法大多只考虑确定性QoS,而忽略现实中QoS的不确定性。文献[8]考虑到不确定的服务质量,将具有不确定QoS的服务组合问题建模为一个区间数多目标优化问题(Interval Number Multi-Objective Optimization Problem, IMOP),并提出了一种基于分解的非确定性多目标进化算法。以上这些方法只考虑组合服务在执行阶段的QoS性能,即组合服务的瞬时QoS性能,而忽略了云环境的不确定性。服务组合的成功在很大程度上取决于不同组件服务保持长期服务质量(QoS)满足用户需求的能力,与传统的服务组合相比,云服务组合通常是从长期角度考虑的。文献[9]定义了一种长期QoS感知云服务组合的方法,引入了三种元启发式算法,即遗传算法(Genetic Algorithm, GA)、模拟退火算法和禁忌搜索算法,以选择具有最佳平均长期QoS的服务；然而,他们认为每个服务的时间序列的长度是固定的,通过随机采样对服务进行选择。

基于以上分析,本文认为云服务组合是一个长期优化过程,在长期优化过程中,由于云环境的动态性,使得服务的QoS可能发生变化,需要在用户长期使用过程中最大化满足用户需求。本文中,首先考虑现实世界中用户对服务的访问规律,即一段时间内单个服务的被访问频率,提出一种基于不确定QoS感知的服务组合时间序列模型,该模型使用不定长时间序列描述一段时间内QoS值的变化,能够准确地描述用户对服务的真实访问记录；其次,提出一种基于不确定QoS模型的改进遗传算法,该算法通过采用锦标赛选择策略改进选择操作,使得种群保持了多样性,提高了群体收敛速度。

1 相关工作

近年来,基于QoS感知的服务选择和组合在面向服务的应用中得到了广泛的关注。一般来说,QoS感知服务组合问题可以分为两类:一是确定QoS感知的服务组合,二是不确定QoS感知的服务组合。对于确定QoS感知服务组合,最流行的方法有整数线性规划(ILP)、混合线性规划(MLP)和人工智能(AI)算法。然而,这些服务组合方法主要针对确定的QoS值,而忽略了现实中QoS的不确定性。文献[10]考虑到服务质量的不确定性,提出了一种不确定QoS感知的服务选择模型,并利用非参数检验和对服务质量的稳定性进行了比较,提出了一种基于简单的目标函数值均值或方差比较的决策模型,并给出了实例分析和原型系统。

云服务组合通常是长期的。文献[11]中考虑服务组合的长期性,从基于用户的角度考虑云服务组合,使用离散贝叶斯网络表示终端用户的经济模型,将云服务组合问题建模为一个影响图问题,并提出了一种基于影响图的云服务组合方法。文献[12]中从长期的角度考虑了服务组合,提出了用时间序列来表示经济模型,然后将云服务组合建模为多维时间序列数据库中的相似搜索问题,并使用QoS属性和QoS关系两种结构来进一步提高相似性搜索方法的效率。文献[13]中提出了一种基于长期经济模型驱动的云服务选择和组合方法,利用QoS历史数据来预测服务提供商的长期QoS行为,利用QoS属性之间的相关性来降低预测值和真实值之间的误差,将预测的时间序列组表示为经济模型,然后将云服务组合建模为相似搜索问题。文献[14]中使用深度循环长期短期记忆(Long Short Term Memory, LSTM)来预测未来的QoS值变化,将预测的QoS值推荐给长期服务组合中的组件和替代品。文献[15]考虑基于时间序列的感知QoS的云计算服务组合,将服务的QoS偏好随时间不断变化的过程纳入云服务组合的研究范围,将云服务组合建模成时间序列的相似度对比问题。

2 问题描述

2.1 相关概念

下面介绍云计算服务组合问题中的一些相关概念,并给出云服务、服务质量、服务组合模型以及组合服务(combined service)的形式化描述。

定义1 云服务。云服务是基于互联网的相关服务的增加、使用和交互模式,通常涉及通过互联网来提供动态易扩展且经常是虚拟化的资源。可用一个二元组表示,S={F,NF},其中F和NF分别代表服务的功能和非功能属性。

非功能属性用QoS表示,所以服务又可以表述为{F,Q},其中Q代表服务的QoS值。

定义2 服务质量。 服务质量指服务的非功能属性,可用一个二元组{RT,TH}表示,其中RT和TH分别代表响应时间(response time)和吞吐量(throughput)。

1)响应时间RT。响应时间是从用户提交服务请求到服务执行完成并返回结果的时间间隔，包括服务执行时间Texe,网络传输时间Ttrans和其他时间花费Toth:

RT=Texe+Ttrans+Toth

2)吞吐量TH。吞吐量是指服务单位时间内可处理的请求数量。

QoS属性可以分为两类:正相关和负相关属性。正相关属性意味着属性值越高,质量越好,例如:可靠性、可用性。负相关属性意味着与正相关属性相反。并且由于QoS中每个元素的取值有较大差异,数值不是一个数量级,因此在进行服务选择和服务组合之前,需要对QoS各属性值进行归一化处理,通常每一个QoS属性转换成0～1的值。因为正相关属性值很容易转换成负相关属性值,为了简单,本文只考虑负相关属性值。本文按以下公式进行归一化处理。

1)效益型：

(1)

2)成本型：

(2)

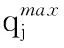
定义3 组合服务(Combined Service, CS)。组合服务是将多个单一服务组合起来构建复杂、功能强大的服务。一个抽象的组合服务可用一个抽象的组合请求表示，CS={S1,S2,…,Sn},其中CS表示请求服务类。一个具体的组合服务可以定义为抽象组合服务的实例化。每个抽象服务类包含功能相同、QoS值不同的服务,通过服务选择将CS中每个抽象服务类实例化,可以得到一个具体的组合服务。组合服务QoS计算方法如表1。本文采用顺序结构模型讨论QoS感知云服务组合问题。

2.2 QoS模型描述

本文考虑的QoS属性为响应时间和吞吐量,分别用q1、q2表示。不同于传统服务组合问题,组合服务的整体QoS性能需要从长期角度衡量。本文采用不定长时间序列描述服务的长期QoS值数据变化,时间序列是指将相同统计指标的数值按其发生的先后顺序排列而成的数列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。现实中,由于云环境的动态变化,服务提供商所提供服务质量可能会发生变化,在不同的时间段内,用户对同一服务具有不同的QoS体验。由于一段时间内每个服务被调用次数不同,为更真实地反映QoS的变化,将服务不确定QoS值表示为TSGm×2:

(3)

服务被调用m次后,其不确定QoS值可以形式化一个时间序列TSGm×2,Qi(i=1,2,…,m)代表某个具体服务在第i次被调用时QoS的瞬时记录,qij(i=1,2,…,m;j=1,2)代表第j个QoS指标在第i次调用时的记录值。

组合服务(CS)的QoS属性用链表表示,记为List(CS)。服务组合中的每个节点表示对应抽象服务下所选择的具体服务,即链表中每个节点代表一个具体的候选服务。

表1 组合服务QoS计算方法Tab.1 QoS computation formula of four basic composition patterns

2.3 目标函数

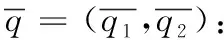
(4)

(5)

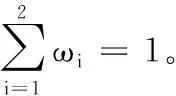
3 算法设计

3.1 基本遗传算法

由于遗传算法(GA)实现步骤简单,并且具有良好的全局收敛能力、自适应能力和并行能力,目前已经被广泛成功地应用于多个领域。基本遗传算法流程如图1所示。

图1 基本遗传算法流程Fig. 1 Flow chart of basic genetic algorithm

采用遗传算法求解服务组合问题的优点是规则简单、编码简单,并且具有较强的全局寻优能力。其缺点是：稳定性差,遗传算法属于随机性算法,需要进行多次运算,结果的可靠性差；易早熟收敛,即对新空间探索能力有限,易收敛到局部最优解。因此,在求解现实问题时,都需要对遗传算法进行适当改进,提高算法效率。

3.2 算法改进策略

文献[9]中将精英选择策略应用到遗传算法,以代替标准遗传算法中的轮盘赌选择策略,并指出精英选择策略具有能够防止最优个体的丢失、提高群体收敛速度等优点。但是,相对于轮盘赌选择策略,精英选择策略每次都需要从种群中选择最好的部分个体,该操作将会使得种群多样性丢失,极易导致早熟收敛,从而降低寻优精度。另外,采用精英选择策略,每次选择都需要对种群所有个体进行排序,时间开销过大,造成运行时间很不理想。为此,本文提出一种改进遗传算法T-GA(Tournament strategy GA),以提高遗传算法的普适性和寻优性能。

T-GA中采用锦标赛选择策略代替基本遗传算法中轮盘赌选择策略,每次进行选择时,适应度较好的个体被选择的概率较大。同时,由于它只是使用适应值的相对值作为选择的标准,而与适应度的数值大小不成直接比例，从而能避免超级个体的影响,在一定程度上既使得种群保持了多样性,防止早熟收敛,又提高了群体收敛速度。

锦标赛选择策略每次从种群中选取出一定数量的个体,然后选择其中最好的一个进入子代种群，重复该操作,直到新的种群规模达到原来的种群规模。具体的操作步骤如下:

1)确定每次选择的个体数量R。

2)从种群中随机选择R个个体(每个个体入选的概率相同),根据每个个体的适应度值,选择其中适应度值最好的个体进入子代种群。

3)重复步骤2)N次,得到的个体构成新一代种群。

3.3 算法描述

实验中,组合服务是一个五元组,即每个CS记录包含五个子服务过程。每个子服务作为染色体上的一个基因位,每个CS包含五个基因位。每个基因位置属于不同的候选服务集。根据适应度函数计算适应度值,通过迭代,本文算法能够找到最优组合方案。本文算法中种群采用实数编码,具体算法描述如下。

算法1 T-GA。

Initializesmembers randomly as populationP

Evaluate each member inP

P′=NULL

while stop criterion not met do

Select (1-Pc)*smembers fromPby tournament and insert intoP′

Randomly selectpc*smembers fromPwith no duplicate

Crossover(Pc)

Insert the offspring intoP′

Randomly selectu*smembers fromP′

for each selected memberido

Mutation(u)

end for

P=P′

Evaluate each member inP

end while

returnbestmember

其中:s为初始种群数量,P为父代种群,P′为子代种群。在选择操作中采用轮盘赌选择策略从种群中选择(1-Pc)*s个父代个体直接遗传到子代,然后,将父代剩余个体进行交叉操作Crossover(Pc),采用单点交叉,其中交叉位置随机产生,将交叉得到的个体保存到子代种群P′中。然后,从P′中随机选择u*s数量的个体进行变异操作Mutation(u),同样,变异位置通过随机产生。通过选择、交叉和变异操作,本文算法不仅能够使得种群保持了多样性,防止早熟收敛,而且提高了种群收敛速度。

4 实验分析

为验证所提出时间序列模型的可行性,以及本文算法T-GA的性能,以公共数据集WSDream[3]为测试数据，将本文算法与基于精英选择策略的遗传算法(Genetic Algorithm based on Elite selection strategy, E-GA)[9]进行对比。

4.1 实验数据与环境

为了使实验更具代表性,实验数据采用Zhang等的公用数据集WSDream[3],包含142个用户在64个时间间隔对4 532个Web服务的响应时间和吞吐量的真实记录值,现实世界中,大部分用户都只调用过少数的Web服务,所以每个服务的真实调用记录并不都包含64个时刻记录。实验环境为: 64位Windows 7 OS,Intel Core i7-4790 CPU @3.60 GHz,4 GB RAM,Visio Studio 2010。

由于数据集较为庞大,需要对数据进行处理,从中选取一部分数据作为实验的真实数据。数据抽取操作步骤如下:

1)从数据源中抽取Service User ID为0的数据。

2)对数据进行降噪处理。

3)将数据集按Web Service ID提取出对应的QoS值时间序列,得到用户0对1 610个Web Service ID的调用QoS值时间序列。

4)按顺序选择前1 500个Web Service ID作为实验数据,将得到的数据集分为5组,每组300个Web Service ID对应的QoS值时间序列,每组中的服务提供相同的功能。

4.2 实验结果与分析

下面评估所提出不定长时间序列(Uncertain-Long Time Series, ULST)模型的可行性和所改进的算法的有效性、效率和稳定性。实验参数设置如表2所示。

表2 实验参数设置Tab.2 Experimental parameter settings

图2 ULST模型可行性Fig. 2 The feasibility of ULST model

4.2.1 ULST模型的可行性

为了验证不定长时间序列模型的可行性,采用4.1节数据处理所得到的数据,从每个服务对应的时间序列中随机选取一个QoS值作为该服务的瞬时访问记录,将得到的数据分为5组,每组300个Web Service ID对应的QoS值瞬时访问记录,每组中的服务提供相同的功能。

图2中:Instant1和Instant2分别代表两次随机操作的结果,即瞬时QoS性能。从图2可以看出,本文方法较瞬时访问结果有所提高。

4.2.2 算法有效性分析

为了进行算法的有效性对比,在如下实验参数设置下进行100次重复实验,取其均值为最终衡量指标,实验结果如表3所示。其中：种群规模为100,迭代次数为500,变异概率为0.15,交叉概率为0.8,QoS的维度为2,任务数量为5,每个任务的候选服务数以50为步长从50递增到300。

从表3可以看出,随着候选服务数量的增加,本文算法获得的最优解优于E-GA[9],表明本文算法的寻优精度高。候选服务数在50和100时,由于候选服务数量少,两种算法都能够收敛到最优解;但随着候选服务数量继续增大,本文算法在收敛精度上具有明显的优势。

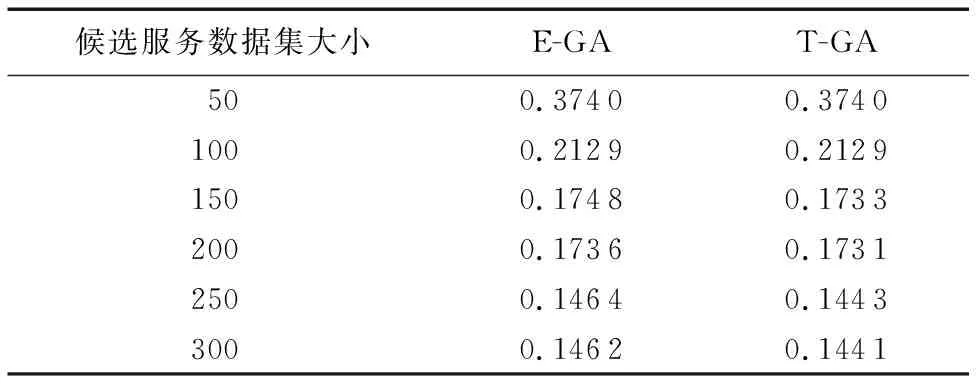
表3 不同候选服务数据集大小的适应度值对比Tab.3 Fitness value comparison with different candidate service dataset sizes

4.2.3 算法的时间效率分析

为进一步分析T-GA和E-GA的时间开销,本文分别进行了两组对比实验:

1)具有不同的种群大小和相同的迭代次数(100)进行优化100次的平均运行时间(如图3(a)所示);

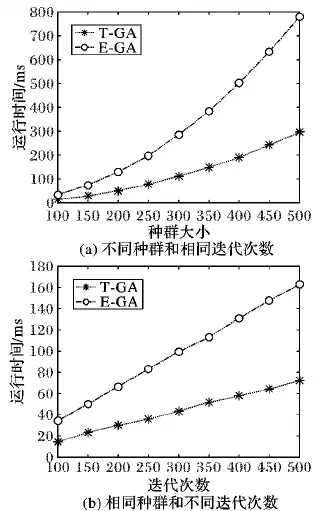
图3 算法在不同实际条件下的平均运行时间对比Fig. 3 Average running time comparison of algorithms under different actual conditions

2)具有相同的种群大小(100)和不同的迭代次数进行优化100次的平均运行时间(如图3(b)所示)。

从图3(a)可以看出,相同迭代次数情况下,随着种群规模的增大,算法运行时间也在增加,且算法的运行时间与种群规模大小呈线性关系；同样,如图3(b),种群大小相同,随着迭代次数的增加,算法运行时间与种群迭代次数呈线性增加。因此,在时间开销方面,本文算法具有E-GA无法替代的优势。

4.2.4 算法稳定性分析

为验证T-GA寻优结果的稳定性,采用均方差(Root Mean Square Error, RMSE)验证不同算法的稳定性。RMSE定义如下:

(6)

其中:xi表示第i次实验结果；x表示n次实验的平均结果。

图4 不同算法的均方差对比Fig. 4 RMSE comparison of different algorithms

从图4可以看出,随着候选服务数的增加,算法的均方差值也在逐渐上升,即稳定性在降低,候选服务数越多,结果越不稳定。实验结果可看出：E-GA寻优结果的波动性较大；而T-GA寻优结果的均方差低于E-GA算法,表明本文算法具有更好的稳定性。

4.2.5 变异概率u的影响

遗传算法中,变异是模拟生物在自然环境中由于各种偶然因素引起的基因突变过程。变异概率u是遗传算法中的重要参数,变异运算是种群产生新个体的辅助方法,决定了遗传算法的局部搜索能力,同时保持种群多样性,避免进化停滞,出现早熟收敛,其概率分布在0.1～1,变异体现了全局最优解的全局覆盖。在遗传算法中,为测试变异概率对算法的影响,设置候选服务规模为300,u的变化为0.1～0.9,步长为0.1。运行100次的平均适应度值的统计结果如图5所示。

从图5可以看出,在相同候选服务规模下,E-GA寻优结果随u的不同而变化；T-GA在不同参数设置下,即使在相应参数变化足够大时,寻优结果仍趋于不变，说明本文算法具有很好的稳定性。

以上实验结果表明：本文提出的ULST模型能够有效地解决不确定QoS感知的云服务组合问题；并且,结合所提出的改进遗传算法T-GA的有效性、效率和稳定性来看,T-GA能够有效地解决不确定性云服务组合优化问题。

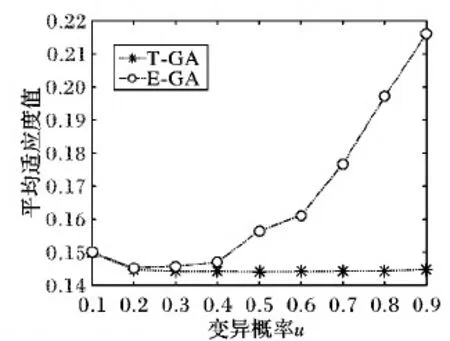
图5 变异概率对平均适应度值的影响Fig. 5 Influence of mutation probability on average fitness value

5 结语

本文研究基于不确定QoS感知的云服务组合问题,首先,提出了一种基于不确定性QoS感知的云服务组合时间序列模型,将服务的QoS值随时间变化过程建模为不定长时间序列,该模型能够准确地描述用户对服务访问的真实记录;其次,采用一种改进的遗传算法找寻最优解,该算法通过引入轮盘赌选择策略改进基本遗传算法选择策略,使得算法能有效地避免早熟收敛,较好地提高算法的全局收敛能力和搜索效率。实验结果表明了本文方法的可行性和有效性。在今后的工作中,将研究跨界服务不确定QoS问题,寻找一种解决复杂不确定性跨界服务系统的优化均衡方法。